761
Technical Committee 103 /
Comité technique 103
very close between the FEM-SSR analysis and the LEM
analysis as seen in Figure 6 and Figure 7.
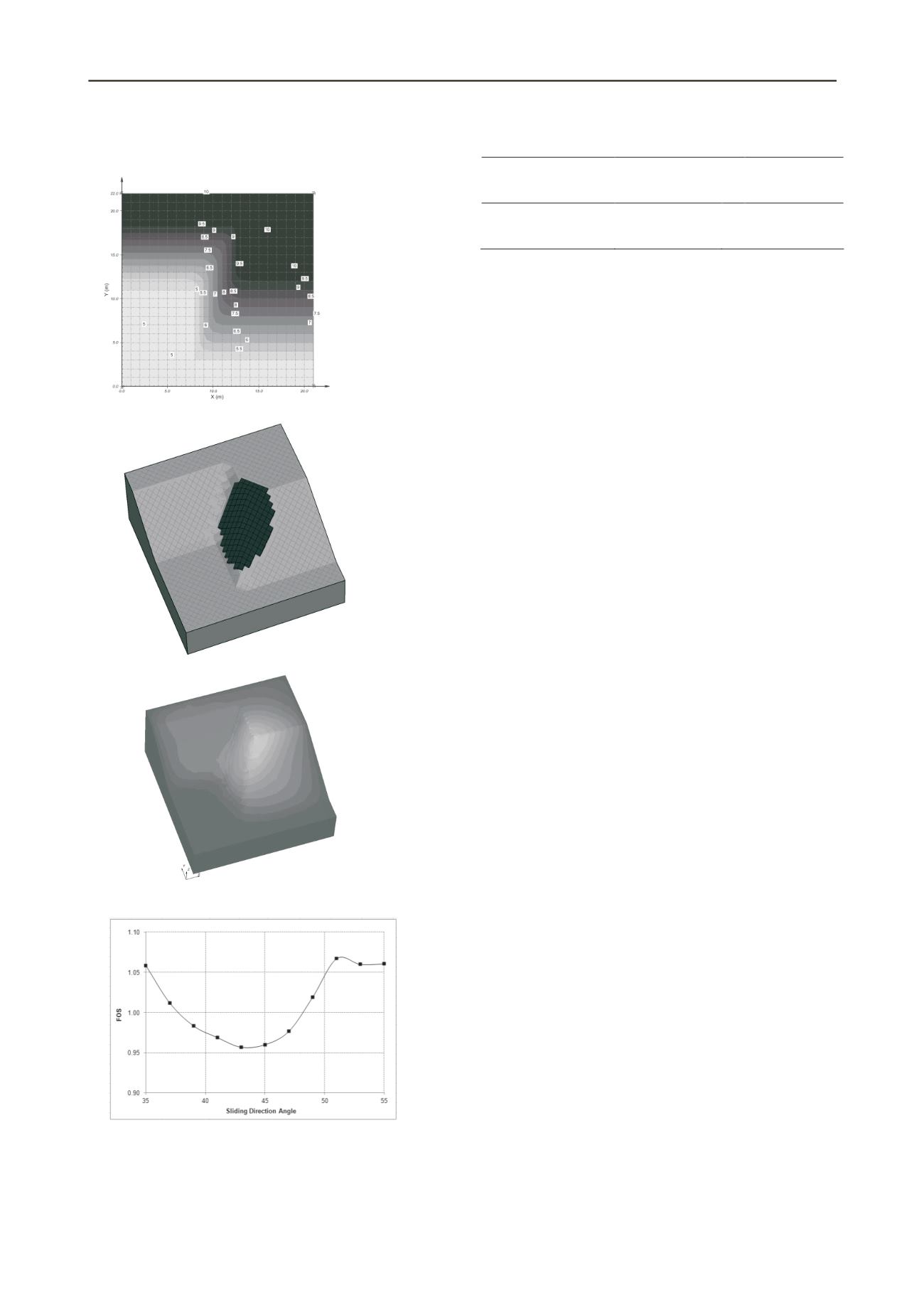
Figure 5. Plan view of elevation contour of Example 2
Figure 6. Critical slip mass of Example 2 from the 3D LEM analysis
Figure 7 Contour of total displacement from FEM-SSR analysis
Figure 8. Plot of rotation angle vs. FOS for Example 2
Table 2. Comparison of 3D FOS for the slope in Example 2
SVSLOPE3D
(LEM)
SVSOLID3D
(SSR)
Jiang( 1997)
(LEM+DP)
0.957 (Bishop),
0.977 (Spencer)
0.941
0.96
3 CONCLUSIONS
An actual slope failure occurs along the most critical sliding
direction that is often unknown for general 3D slopes.
Determination of the critical slip surface and its FOS involves
the search for the criticl sliding direction. One of the advantage
of FEM-SSR technique is that it does not need to specified the
sliding direction in advance, however it can not give the exact
sliding direction angle value either. SVSLOPE 3D provides an
optimizaton technique that can find the critical sliding direction
as part of FOS search.
Based on Example 1 it can be seen that both the failure slip
surface shape and FOS values from the FEM-SSR result and the
3D LEM result match well with the Wei et al. (2009) result. The
second example also demonstrates the similarity of results
between analyzing a complex 3D slope stability geometry
where the direction of the slip may have an effect on the
calulated FOS.
These results demonstrate the usefulness of both 3D LEM and
FEM-SSR methodologies for the analysis of slope geometries
and loading conditions which are fundamentally 3D in nature.
4 REFERENCES
Baker R. 1980. Determination of the critical slip surface in slope
stability computations.
Int. J. for Numerical and Analytical
Methods in Geomechanics
, 4, 333-359.
Cheng Y.M. 2003. Locations of critical failure surface and some further
studies on slope stability analysis. Computers and Geotechnics 30
(3), 255
–
267.
Cheng Y.M., Liu H.T., Wei W.B. and Au S.K. 2005. Location of
critical three-dimensional non-spherical failure surface by NURBS
functions and ellipsoid with applications to highway slopes.
Computers and Geotechnics
32 (6), 387-399.
Griffiths D.V. and Lane P.A. 1999, Slope stability analysis by finite
elements,
Géotechnique
, 49 (3), 387-403.
Griffiths D.V. and Marquez R.M. 2007. Three-dimensional slope
stability analysis by elasto-plastic finite elements,
Géotechnique
, 57
(6), 537
–
546.
Hovland H.J. 1977. Three-dimensional slope stability analysis method.
J Geotech Eng Div
, ASCE 103 (9), 971
–
986.
Hungr O., Salgado F.M. and Byrne P.M. 1989. Evaluation of a three-
dimensional method of slope stability analysis.
Canadian
Geotechnical Journal
, 26 (4), 679
–
686.
Jiang J.C. 1997. Determination of the three-dimensional critical slip
surface in slope stability analysis,
PhD thesis
, the University of
Tokushima, Tokushima, Japan.
Lam L. and Fredlund D.G. 1993. A general limit equilibrium model for
three-dimensional slope stability analysis,
Canadian Geotechnical
Journal
,30 (6), 905
–
919.
Wei W.B., Cheng Y.M. and Li L. 2009. Three-dimensional slope failure
analysis by the strength reduction and limit equilibrium methods,
Computers and Geotechnics
, 36 (1-2), 70
–
80.
Yamagami T. and Jiang J.C. 1997. A search for the critical slip surface
in three dimensional slope stability analysis.
Soils and Foundation
37 (3), 1
–
6.
Zhang X. 1988. Three-dimensional stability analysis of concave slopes
in plan view,
J. Geotech. Engng
, ASCE, 114 (6), 658
–
671.
3
FEM-SSR analysis is 0.941. The contour of the final
displacement at the final stage is shown in Figure 7. The critical
slip mass based on 3D LEM analysis is shown in Figure 6. The
FOS is 0.957 and 0.977 separately for Simplified Bishop and
Spencer method. The critical slip direction also needs to be
found. As shown in Figure 8, the critical slip surface direction is
43 degree counter-clock wise from the negative x direction. It
can be seen clearly that both the shape and slip direction are
very close between the FEM-SSR analysis and the LEM
analysis as seen in Figure 6 and Figure 7.
Figure 5. Plan view of elevation contour of Example 2
Figure 6. Critical slip mass of Example 2 from the 3D LEM nalysis
Figure 7 Contour of total displacement from FEM-SSR nalysis
Figure 8. Plot of rotation angle vs. FOS for Example 2
Table 2. Comparison of 3D FOS for the slope in Example 2
SVSLOPE3D
(LEM)
SVSOLID3D
(SSR)
Jiang( 1997)
(LEM+DP)
0.957 (Bishop),
0.977 (Spencer)
0.941
0.96
3
CONCLUSIONS
An actual slope failure occurs along the most critical sliding
direction that is often unknown for general 3D slopes.
Determination of the critical slip surface and its FOS involves
the search for the criticl sliding direction. One of the advantage
of FEM-SSR technique is that it does not need to specified the
sliding direction in advance, however it can not give the exact
sliding direction angle value either. SVSLOPE 3D provides an
optimizaton technique that can find the critical sliding direction
as part of FOS search.
Based on Example 1 it can be seen that both the failure slip
surface shape and FOS values from the FEM-SSR result and the
3D LEM result match well with the Wei et al. (2009) result. The
second example also demonstrates the similarity of results
between analyzing a complex 3D slope stability geometry
where the direction of the slip may have an effect on the
calulated FOS.
These results demonstrate the usefulness of both 3D LEM and
FEM-SSR methodologies for the analysis of slope geometries
and loading conditions which are fundamentally 3D in nature.
4
REFERENCES
Baker R. 1980. Determination of the critical slip surface in slope
stability computations.
Int. J. for Numerical and Analytical
Methods in Geomechanics
, 4, 333-359.
Cheng Y.M. 2003. Locations of critical failure surface and some further
studies on slope stability analysis. Computers and Geotechnics 30
(3), 255
–
267.
Cheng Y.M., Liu H.T., Wei W.B. and Au S.K. 2005. Location of
critical three-dimensional non-spherical failure surface by NURBS
functi s and ellipsoid with applications to highway lopes.
Computers and Geotechnics
32 (6), 387-399.
Griffiths D.V. and Lane P.A. 1999, Slope stability analysis by finite
elements,
Géot chnique
, 49 (3), 387-403.
Griffiths D.V. and Marquez R.M. 2007. Three-dimensional slope
stability analysis by elasto-plastic finite elements,
Géotechnique
, 57
(6), 537
–
546.
Hovland H.J. 1977. Three-dimensional slope stability analysis method.
J Geotech Eng Div
, ASCE 103 (9), 971
–
986.
Hungr O., Salgado F.M. and Byrne P.M. 1989. Evaluation of a three-
dimensional method of slope stability analysis.
Canadian
Geotechnical Journal
, 26 (4), 679
–
686.


