756
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
p’ is constant in undrained loading. The behavior changes when
the initial yield locus is reached and the clay begins to yield.
The direction of the undrained stress path is then determined by
the tendency of the clay fabric to compress or dilate. The
direction and shape of the stress path (and at the same note, the
amount of excess pore pressure) depends on several factors such
as the shape and size of the initial yield surface, initial stress
state and the rate of loading.
According to Länsivaara (1999) a high strain rate results in
less excess pore pressure than a comparably lower strain rate
due to effects related to undrained creep. The result of this
behavior is that high strain rates result in higher undrained shear
strength than comparably lower rates.
2.1
Failure pore pressure in LEM
In conventional undrained c’-φ’ calculations there is an inherent
overestimation of shear strength when for any factor of safety F
> 1. This is caused by the fact that for a given loading the
mobilized excess pore pressure is used in calculating the
equilibriums and shear strength. This approach disregards the
further increase of excess pore pressure between the mobilized
stress state and failure (which is not a problem in drained
calculations).
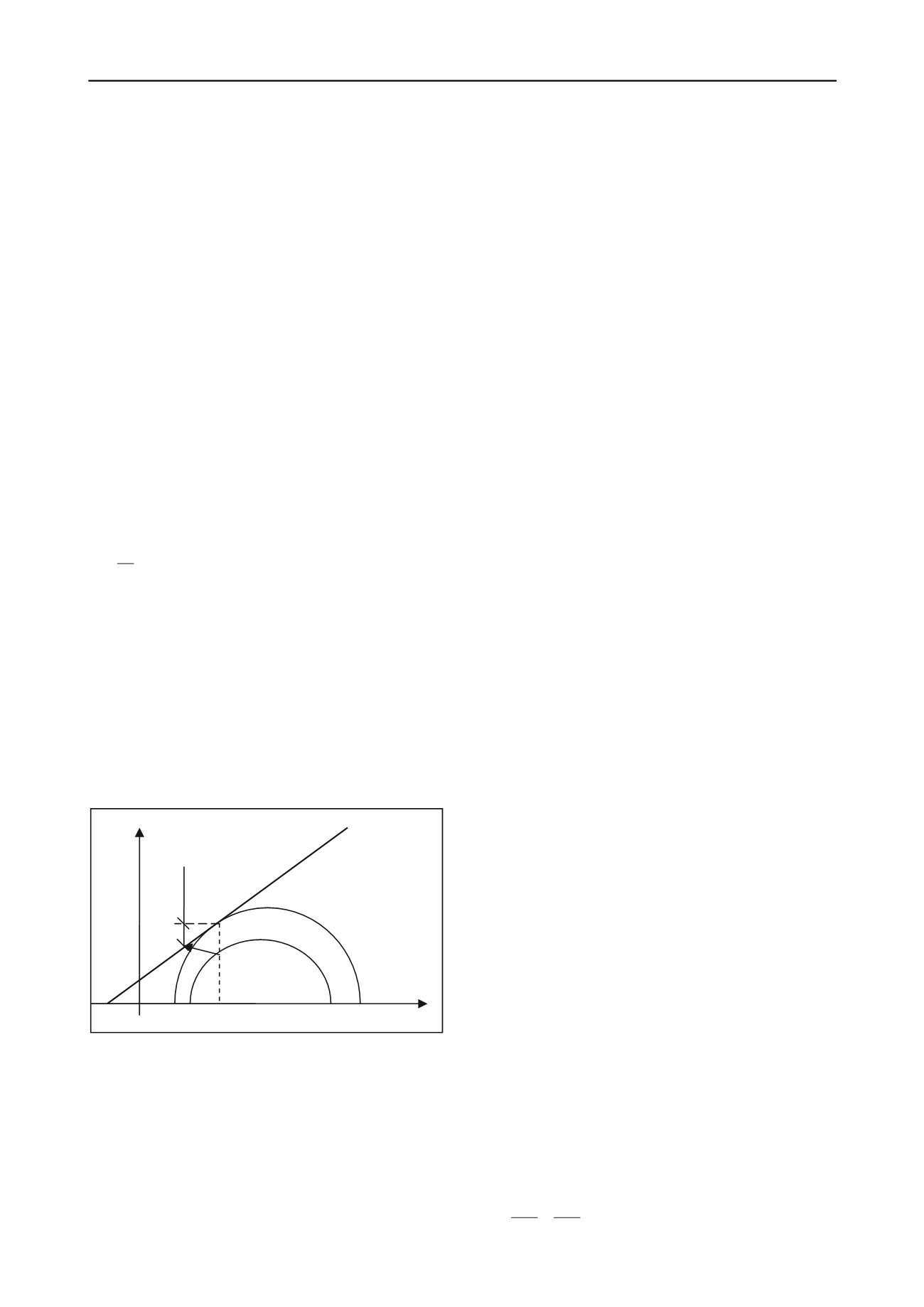
Shear stress is traditionally defined in LEM as:
e
f
F
(1)
where τ
e
is the equilibrium shear stress, τ
f
the corresponding
shear strength and F the factor of safety. This definition implies
a very specific stress path that is highly unrealistic in undrained
loading, for example under an embankment. (Tavenas et al
1980).
The corresponding definition of shear stress effectively
compares the mobilized shear stress τ
e
to an unrealistically
large strength τ
f
that can never be attained because of further
pore pressure buildup between the mobilized state and failure
(Figure 2). This pore pressure behavior is common for soft
normally consolidated or slightly overconsolidated clays that
generally exhibit compressive behavior.
Figure 1. Overprediction of shear strength in typical undrained effective
stress calculations. (Länsivaara et al 2011)
Consequently the definition of the factor of safety in undrained
c’-φ’ calculations is actually different from the factor of safety
in φ = 0 calculations. In φ = 0 calculations the mobilized shear
stress τ
e
is always compared to a value of s
u
that represents the
shear strength τ
fe
that can actually be mobilized for a given set
of physical conditions (consolidation, rate and direction of
shearing etc). The two otherwise conflicting definitions coincide
at F = 1. As a conventional undrained c’-φ calculation for soft
clays will overestimate shear strength when F > 1, one cannot
even in theory expect the same result from a corresponding φ =
0 calculation (Leroueil et al 1990).
In light of this issue it is not enough just to accurately model
the mobilized excess pore pressure, but the implicit
overestimation of the factor of safety should also be taken into
account if possible. At the least, the designer needs to be aware
of these theoretical differences between the two methods and
interpret the results accordingly.
A proposed workaround for the overestimation of shear
strength is to universally use failure state pore pressure in the
calculation even for F > 1, regardless of the actual mobilized
pore pressure. This can be achieved in LEM if the effective
stress path from the initial state to failure (and the
corresponding excess pore pressure) can be approximated. In
(σ’
n
, τ) stress space this assumption places the effective normal
stress to its value at failure, thus giving the ability to compare
the shear stress with the shear strength at failure.
Since τ and F are co-dependent in LEM the mobilized shear
stress τ in the “failure pore pressure formulation” will be
slightly different from the corresponding “traditional” pore
pressure formulation. Whether the difference will be positive or
negative depends on several factors. According to studies with
the method “MUESA” (section 2.3) the induced error on the
factor of safety is small when compared to the overestimation of
shear strength caused by the traditional use of mobilized pore
pressure.
What the use of failure pore pressure does is effectively to
substitute an “incorrect” effective normal stress to obtain a more
realistic calculated shear strength. In LEM this can be
considered an acceptable tradeoff as the main purpose of LEM
is to obtain the factor of safety. If applied correctly, the shear
strength and thus the factor of safety will have a more realistic
value for F > 1 (when compared to the traditional approach of
using mobilized pore pressure). At F = 1 the two different
approaches coincide.
Two calculation methods for modeling the amount of yield-
induced pore pressure in undrained effective stress LEM
calculations are proposed in the following section. Both
methods employ an anisotropic yield surface to describe the
change of effective mean stress when clay is loaded to failure.
2.2
Method 1: r
u
’
The method r
u
’ was developed for normally consolidated clays.
It should be considered as a simple engineering tool to model
yield-induced pore pressured for stability calculations of old
embankments.
Finnish soft clays are usually only very slightly
overconsolidated, mainly due to aging. Under old embankments
the clays have generally become normally consolidated.
If failure occurs, excess pore pressure will thus have
developed corresponding to a stress change from the initial in
situ state at the K
0NC
line to the failure state. The most critical
event corresponds to slow loading or long loading time allowing
for the yield induced pore pressure to develop. Excess pore
pressure from yielding can now be simply calculated as the
horizontal difference of the intersection of K
0
-line with the
initial yield surface, and the intersection of the failure line with
the yield surface in the (p’, q) stress space. For this a proper
estimation of the yield surface is needed. It has been shown
(Länsivaara 1995, Länsivaara 1999) that the initial yield surface
can be estimated by knowing only the friction angle and the
preconsolidation pressure of the clay.
This can further be utilized by applying a pore pressure
parameter similar to the generally used r
u
, with the exception
that it now stands for yield induced pore pressure and should be
applied to effective vertical stress. This pore pressure parameter
is refe d as r
u
’ and is defined as:
rre
) ,'
(
'
1
'
'
0
0
0
v
v
v
ey
u
f
u
r
(2)
Failure state
Equilibrium state
’
n
’
f
e
fu
Overprediction
of strength


