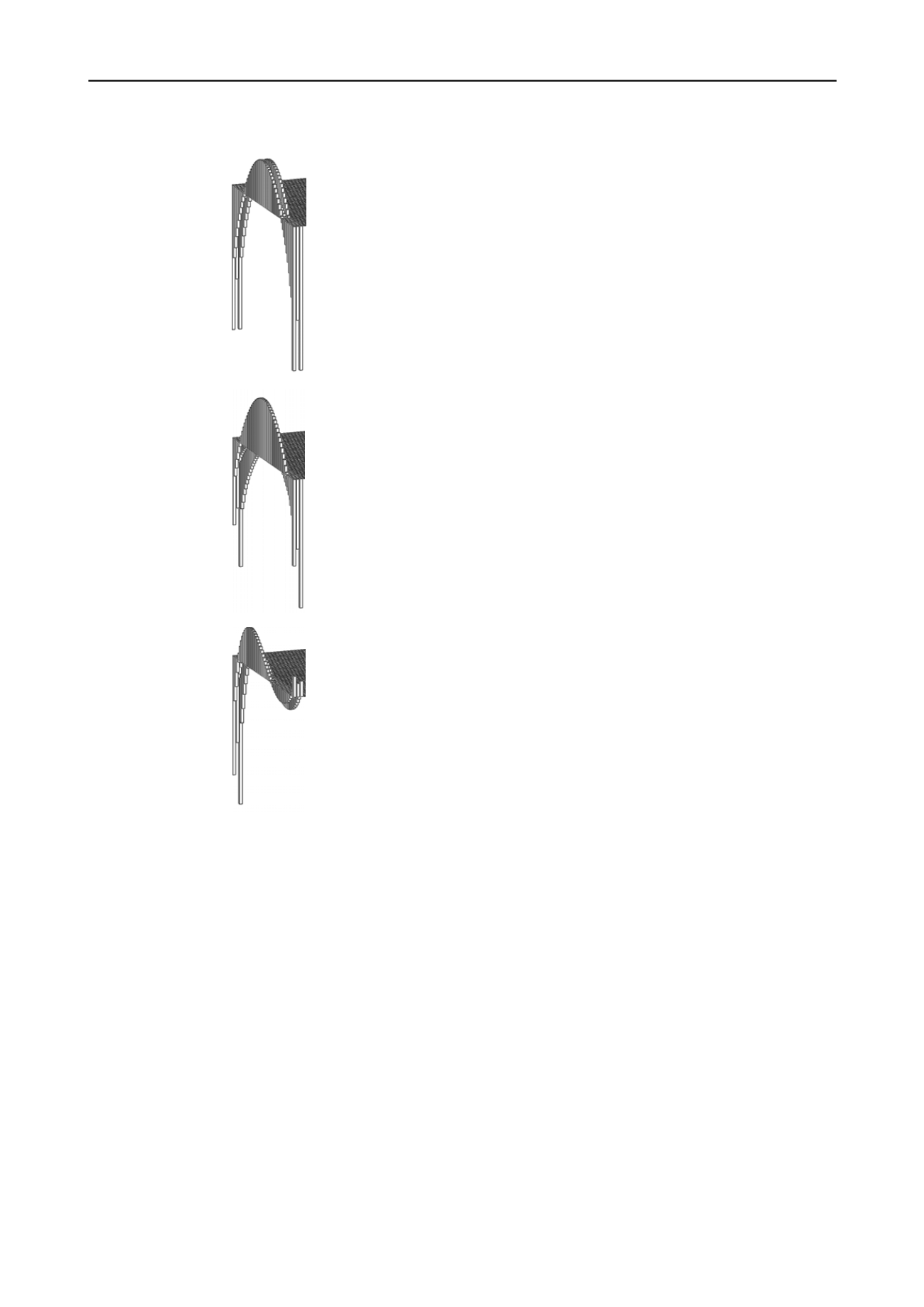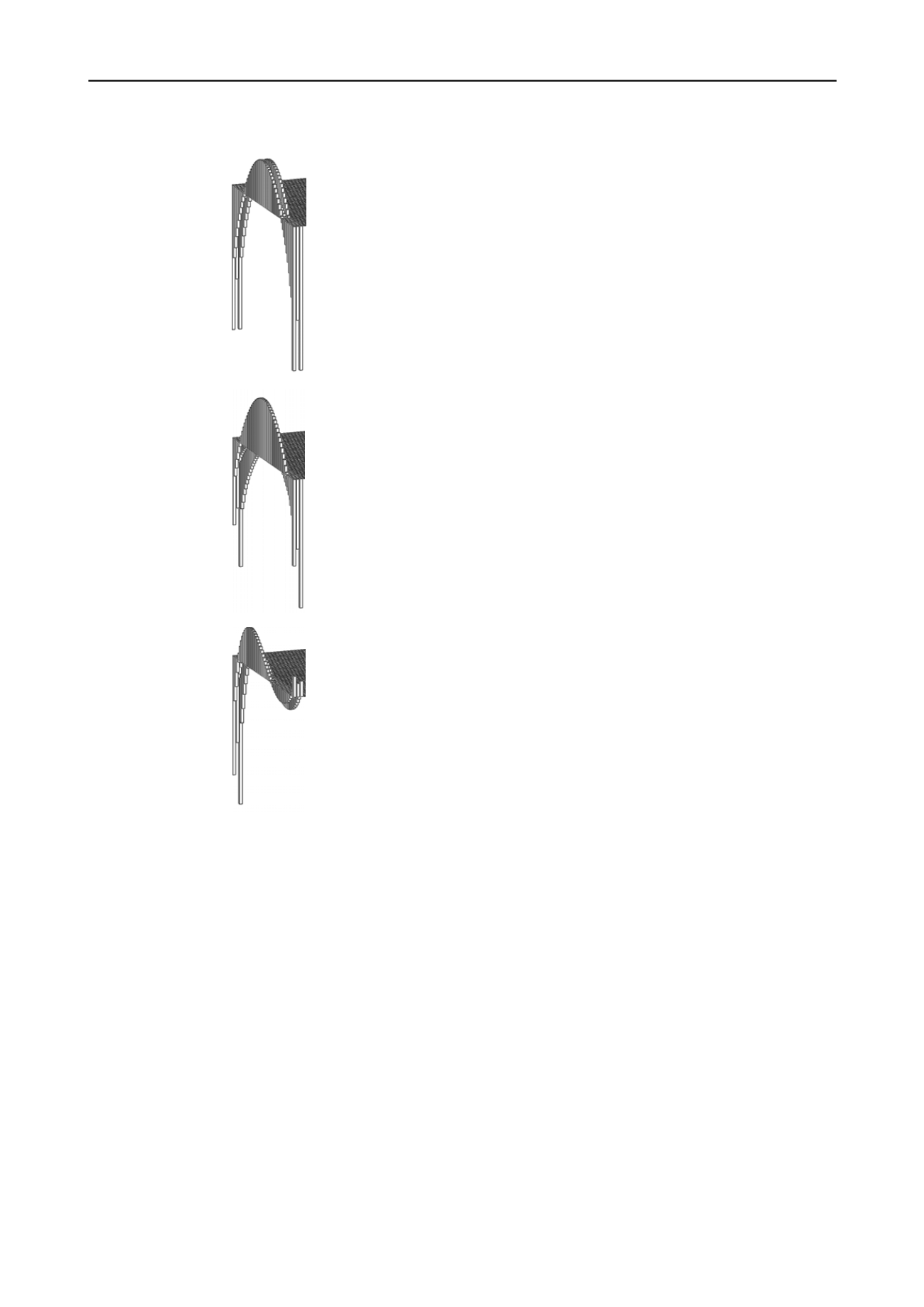
750
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
(1)
A similar (from the geomechanical viewpoint) approach to
calculation of beam-like structures on soil deformed by
subsurface works was developed in (Pushilin and
Sheynin 2006), where the model was confined to the planar
case. This approach allows allows to write down an ordinary
differential equation for the beam deflection and formulate a
finite-difference algorithm of its solution. Stresses in a beam-
like structure on Winkler foundation whos deformations are
induced by a nearby excavation are determined in, e.g.
(Ilyichev e.a. 2006).
6 CONCLUSION
A numerical method was developed for the solution of soil-
structure interaction problems of elongated deformable
structures (rigid in transversal direction) on linear half-space. It
was supposed that soil is deformed under the effect of additional
outer sources, e.g. tunnelling. Numerical results were obtained
for the most practically typical special case, when the structure
may be modeled by a beam with finite bending stiffness in
longitudinal direction and infinitely rigid and of finite breadth in
transversal direction. The cases of load application both on the
structure and on the soil continuum due to tunnelling were
considered. Results for different beam stiffness and tunnel-
structure layout are obtained and analyzed.
(2)
7 REFERENCES
Attewell P.B., Yeates J., Selby A.R. 1986.
Soil movements induced by
tunnelling and their effects on pipelines and structures
. Glasgow,
Blackie.
(3)
Biot M.A. 1937. Bending of an infinite beam on an elastic foundation.
Publications from the Graduate School of Engineering, Harvard
Univ
. (203).
Finlayson B.A. 1972.
The method of weighted residuals and variational
principles
. Academic Press, New York.
Fischer F.D., Gamsjäger D. 2008. Beams on foundation, Winkler
bedding or halfspace — a comparison.
Technische mechanik.
28 (2), 152-155.
Gorbunov-Posadov M.I., Malikova T.A., Solomin V.I. 1984.
Calculation of structures on elastic bed
. Stroyizdat, Moscow.
Рис. 3. Contact pressure due to tunnelling under the footing of the beam
with flexibility index
t
= 1 on the half-space
Il'ichev V.A., Nikiforova N.S., Koreneva E.B. 2006. Method for
calculating bed deformations of buildings near deep excavations.
Soil Mechanics and Foundation Engineering
. 43 (6), 189-196.
Karamansky T.D. 1981.
Numerical methods of structural mechanics
.
Stroyizdat, Moscow.
Results are obtained for three cases (see Figure 3):
(1) Symmetrical layout with long tunnel perpendicular to
the longitudinal axis of the structure:
x
0
=0;
x
i
= 1000;
x
f
= 1000;
= 90º.
Kholmyansky M.L. 2007. On the load distribution among separate
foundations.
Proc. of RSSMGFE 50-th anniversary conference.
RSSMGFE
, 2, 160-164.
(2) Tunnelling up to the structure axis perpendicular to the
longitudinal axis of the structure. Parameters are the same as in
case (1) except
x
f
= 0.
Klar A., Vorster T.E.B, Soga K., Mair R.J. 2004. Soil-pipe-tunnel
interaction: comparison between Winkler and elastic continuum
solutions.
Technical Report of the University of Cambridge
CUED/D-SOILS/TR 332
. Cambridge.
(3) Tunnelling with the angle
= 60º to the longitudinal axis
of the structure up to the end of the structure:
x
0
=0;
x
i
= 25.5;
x
f
= –10.
Pushilin A.N. and Sheynin V.I. 2006. Assessment of stress in the
structures arising from construction of underground opening.
75th
anniversary of NIIOSP (Proc. of NIIOSP)
, 66-73.
Terzaghi K. 1943.
Theoretical soil mechanics
. Wiley, New York.
In all the cases there are no effects on the structure except
soil induced effects, so contact stresses are self-equilibrated. In
the case (1) there are two axes of symmetry, in case (2) — only
one.
Vesic A.S. 1961. Bending of beams resting on isotropic elastic solid
J.
Eng. Mech. Div.
87 (EM2), 35-53.
Zhemochkin B.N. and Sinitsyn A.P. 1947.
Practical methods of
calculation for beams and slabs on elastic foundation without using
the Winkler hypothesis
. Gosstroyizdat, Moscow.