740
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
models (or Meta models) have been integrated with GA to
optimize different management schemes to limit seawater
intrusion. These studies have generally focused on controlling
progressive advancement of saline water, mainly in the two
dimensional areal section. Maximization
of the total pumping
rate from wells, minimization of the total recharge rate into
wells and minimization of the total amount of concentration in
the aquifer are the major objective functions of these studies
(e.g., Sreekanth and Datta, 2010 ; Dhar and Datta, 2009; EL-
Ghandour et al., 2008; Eusuff and Lansey, 2004; Gordu et al.,
2001 and Cedeno and Vemuri, 1996).
This study presents the development of a coupled transient
density-dependent finite element model for simulation of fluid
flow and solute transport in soils and its application to simulate
seawater intrusion in coastal aquifers. In order to effectively
determine the optimal solution for control of seawater intrusion
the simulation model is integrated with a GA optimization
model to examine three scenarios: abstraction of brackish water,
recharge of fresh water, and combination of abstraction,
recharge and desalination (ADR). The objectives and
constraints of these management scenarios include minimizing
the capital and operation costs, minimizing salt concentrations
in the aquifer, and determining the optimal depth, location, and
abstraction/ recharge rates of the wells.
2 SIMULATION-OPTIMIZATION METHODOLOGY
In this work, an in-house finite element model,
(Saturated/Unsaturated Fluid flow and solute Transport -
SUFT), has been used to study saltwater intrusion in coastal
aquifers. The model uses a hybrid finite element and finite
difference methods to solve density-dependent flow and
transport mass balance equations. The model can handle a wide
range of real-world problems including the simulation of
groundwater flow and solute transport separately and coupled
fluid flow and solute transport, in addition to saltwater intrusion
in coastal aquifers. It has been validated against a number of
case studies from the literature. The details of mathematical
formulation and numerical implementation of the model can be
found in Abd-Elhamid and Javadi (2011). In addition, an
optimization model based on a simple genetic algorithm (GA)
was integrated with the simulation model to optimize the
arrangements for control of seawater intrusion. The GA has
been used, as a powerful search and optimization algorithm, in
many fields of engineering. It consists of some procedures that
search for solutions of complex optimization problems based on
the Darwinian theory of “survival of the fittest” where the
strongest offspring in a generation are more likely to survive
and reproduce. In this technique an initial set of possible
solutions (initial population) is randomly generated. Each
member of the initial population is encoded as a chromosome
with binary bit string. Cycles of evaluation, selection, crossover
and mutation are repeated in an iterative process, where the
population of chromosomes evolves to make a new generation
in each cycle. The chromosomes for the optimal solution are the
final outcome of these cycles (Sivanandam and Deepa, 2008).
In the developed simulation-optimization process, the GA
repeatedly calls the SUFT model to compute state variables
(pressure head and concentration) for different sets of generated
design variables. After computing the objective function and
evaluating its fitness, the processes of selection, crossover, and
mutation are performed in the GA procedure to update the
values of decision variables. The new values of decision
variables are then returned to SUFT and the process is repeated
until it satisfies optimal criteria or it reaches the maximum
generation number.
3 APPLICATION
The simulation-optimization model was applied to one of the
most popular benchmark problems in seawater intrusion in
coastal aquifers, widely known as Henry’s saltwater intrusion
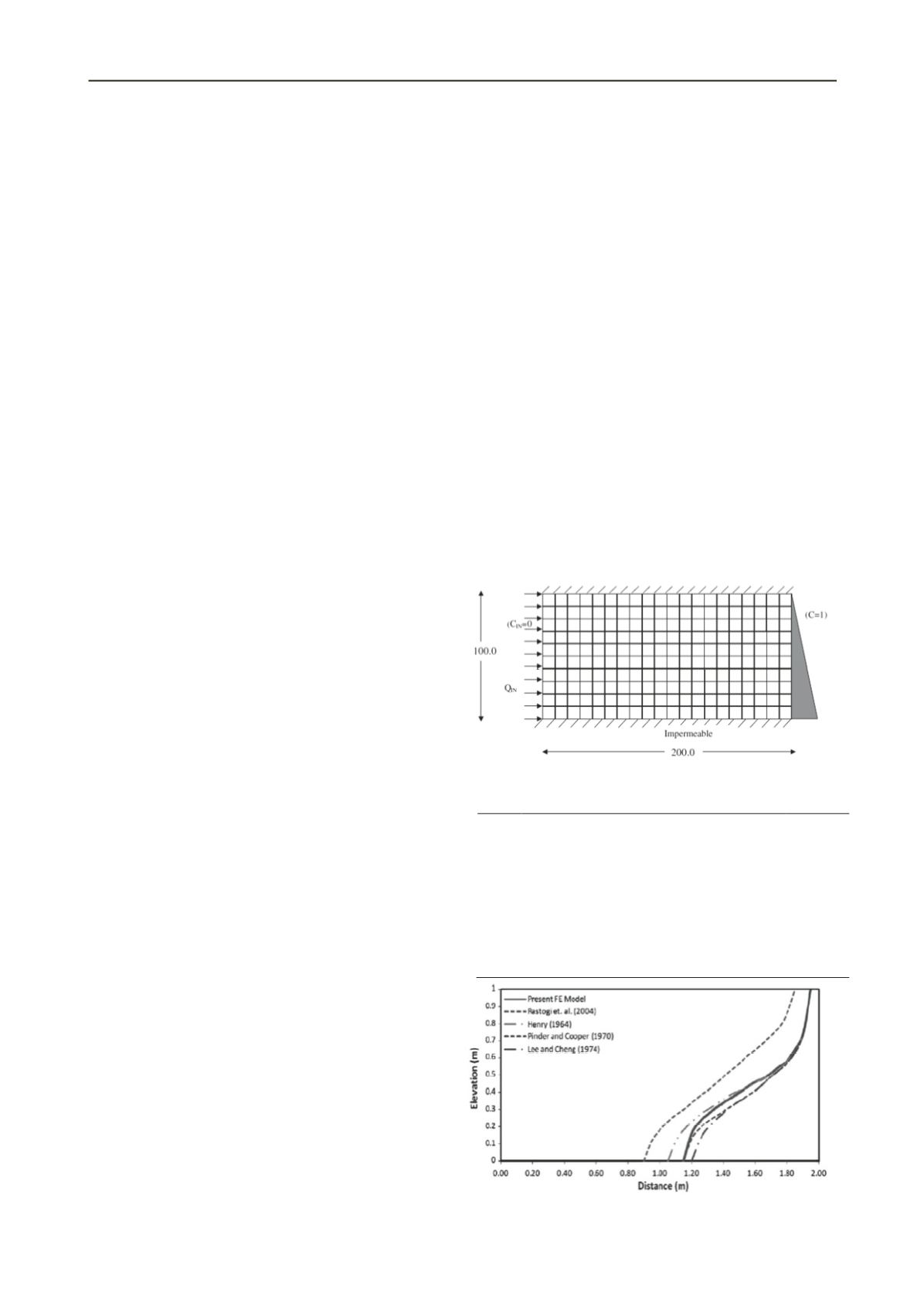
problem. Henry's problem involves seawater intrusion in a
confined aquifer, subject to three different boundary conditions:
constant recharge flux of freshwater on the left boundary,
hydrostatic seawater pressure on the right boundary and
impermeable boundaries along the top and bottom of aquifer as
shown in Figure (1). The parameter values used for numerical
simulations are summarized in Table (1). The aquifer domain is
represented by 661 nodes and 200 quadrilateral isoparametric
elements, each of size 10 m by 10 m. The domain considered is
100 m high and 200 m long. Freshwater concentrations (c=0)
and natural steady-state pressures are set as the initial conditions
everywhere in the aquifer. The problem is analyzed using the
developed finite element model, and the results are compared
with some results reported in the literature. The seawater wedge
is chosen to be represented by 0.5 isochlor, which is an
approach adopted by many researchers.
Rastogi et al. (2004) considered the dispersion coefficients to
be velocity dependent under steady state conditions and selected
values for longitudinal and transverse dispersivities as 0.5 and
0.1 m respectively. The same approach is used in the current
work and the results are compared with a number of known
solutions from the literature. Figure (2) shows these results in
terms of the position of 0.5 iso-concentration lines.
Figure 1. Boundary conditions of Henry’s problem
Table 1. The parameters used in Henry’s problem
Figure 2. 0.5 Isochlor lines for steady-state variable dispersion
D
m
: coefficient of water molecular diffusion [m
2
/ s]
6.6*10
-6
Q
in
: inland fresh water flux [m
3
/sec]
6.6*10
-5
k
: permeability [m
2
]
1.0 *10
-9
n
: porosity [-]
0.35
g
: gravitational acceleration [m / s
2
]
9.8
ρ
w
: density of fresh water [kg/m
3
]
1000
ρ
s
: density of sea water [kg/m
3
]
1025
ρ
o
: density of fresh water [kg/m
2
]
1000
: fluid viscosity [kg / (m.s)]
0.001
α
T
,
α
L
: transverse and longitudinal dispersivity [m]
0.0


