758
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
A same slip surface that approximates the actual failure
geometry in the experiment was used for all calculations (Figure
4). All calculations were made with the Morgenstern-Price
method with interslice force function f(x) = sin (x).
In the r
u
’ calculation additional excess pore pressure from
the loading was modeled to ensure realistic shear strength in the
loaded slices. The MUESA calculation modeled the
overconsolidation POP = 20 kPa in the clay layer, while the r
u
’
calculations assumed normally consolidated conditions as
described in Section 2.1. In addition, a φ = 0 calculation was
made using s
u
values measured with vane shear testing.
Table 2 compares the factor of safety at 30 kPa external load,
as well as the magnitude of the failure load.
It is seen that results (Table 2) with both new methods are
plausible and in fairly good agreement both with the results of
the φ = 0 calculation and actual observations from the
experiment. It must however be noted that the φ = 0 calculation
is still subject to inaccuracies and uncertainties of its own, but
here the extensive soil investigations reduce the uncertainties
involved.
Table 2. Calculation results.
F for 30 kPa load
Failure load
[kPa]
r
u
’
1,43
74
MUESA
1,37
64
s
u
1,48
71
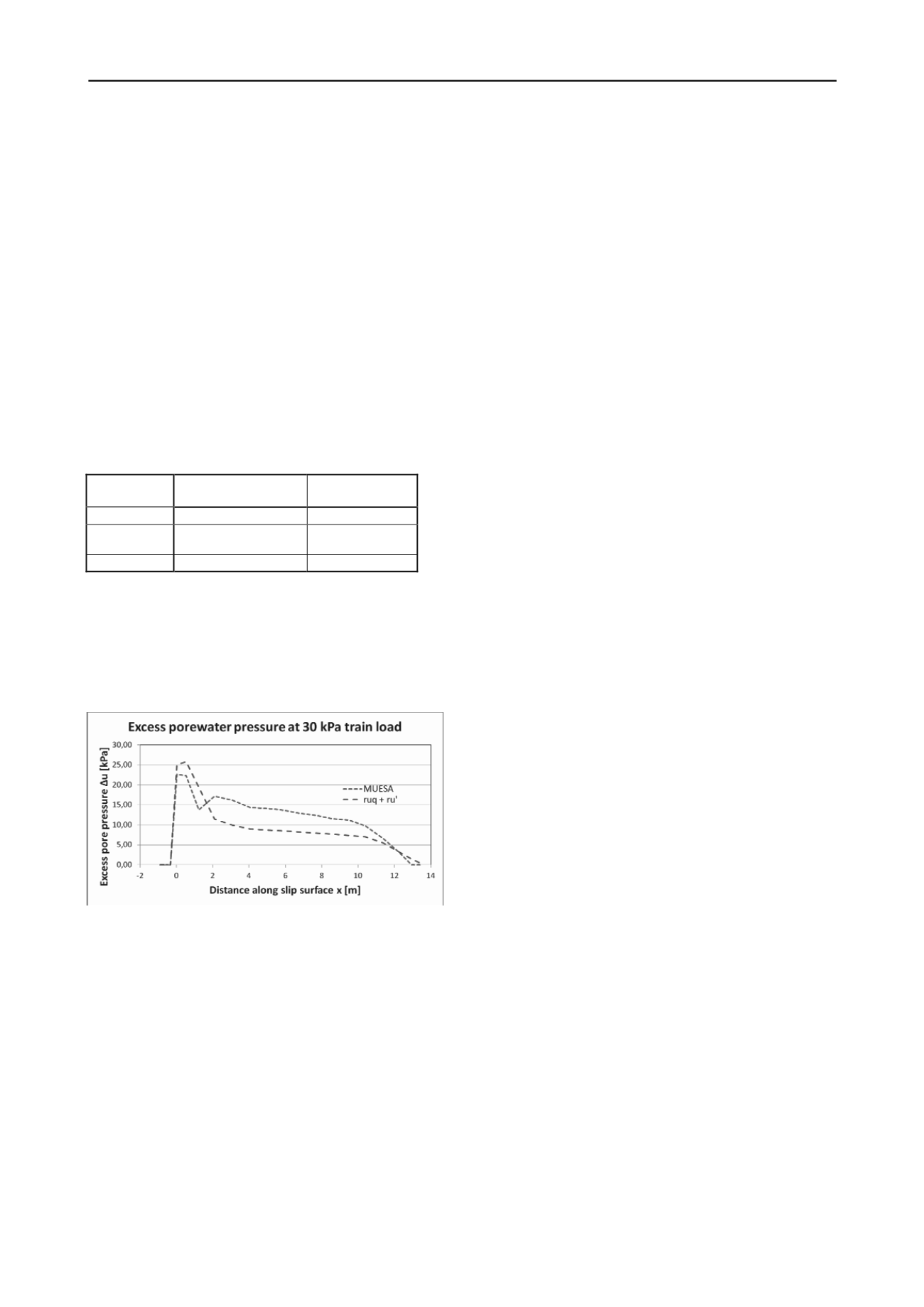
The calculated excess pore pressure levels (Figure 5) are
reasonably close to what was measured at the site before failure
(taking into account how LEM does not distribute excess
loading). At failure excess pore pressures of 10...15 kPa were
measured on the centre part and passive end of the failure zone,
while much higher pressures were measured under the
embankment.
Figure 4. Calculated excess pore pressure levels for load q = 30 kPa
The test embankment eventually failed at a load of 87 kPa.
Many factors lead to this high failure load, one of the most
significant being the time-dependency of pore pressure increase.
It has been estimated that the failure could well have occurred at
a load of ca. 70 kPa, if enough time would have been given for
pore pressure to develop at that load level.
MUESA in its current development state has a tendency to
overestimate the excess pore pressure because volumetric
hardening is not accounted for. This will be rectified in
upcoming versions.
4
CONCLUSIONS
In this paper a concept of universally using failure pore pressure
in undrained effective stress calculations is proposed. Two
calculation methods for modeling excess pore pressure in
undrained effective stress stability calculations are presented.
The methods are intended as simple and effective calculation
tools for basic design purposes.
The method r
u
’ offers a simple pore pressure parameter for
modeling yield-induced excess pore pressure at failure.
The method MUESA is used to take into account the various
factors that affect excess pore pressure in undrained c’-φ’
calculations. It also makes it possible to universally use failure
pore pressure. This makes the calculation theoretically
comparable to φ = 0 calculations. MUESA is still in
development stage, and will be refined further.
These new calculation methods offer an analytical approach
to modeling excess pore pressure in LEM. While they cannot
take into account all the factors that an ideal FEM calculation
could, they can nevertheless be considered very useful and
effective engineering tools.
5
ACKNOWLEDGEMENT
The authors thank the Finnish Transport Agency for the funding
of the research project.
6
REFERENCES
Lehtonen, V. (2011). Instrumentation and analysis of a railway
embankment failure experiment. Research reports of the Finnish
Transport agency 29/2011, Finnish Transport Agency
Leroueil, S., Magnan, J-P. & Tavenas, F. (1990). Embankments on soft
clays. Ellis Horwood Ltd, 360 p.
Länsivaara, T. (2010). Failure induced pore pressure by simple
procedure in LEM. In: Benz, T. et al. (eds.). Numerical Methods
in Geotechnical Engineering. Proceedings of the Seventh
European Conference on Numerical Methods in Geotechnical
Engineering Numge 2010, Trondheim, Norway, 2-4 June, 2010 pp.
509-514.
Länsivaara, T. (1999). A study of the mechanical behavior of soft clay.
Doctoral thesis, Department of Geotechnical engineering, NTNU
Trondheim
Länsivaara, T. (1995). A critical state model for anisotropic soft soils.
Proceedings of the 11th European Conference on Soil Mechanics
and Foundation Engineering, ECSMFE, Vol. 6, Copenhagen.
Länsivaara, T., Lehtonen, V. & Mansikkamäki, J. (2011). Failure
induced pore pressure, experimental results and analysis. 2011 Pan-
Am CGS Geotechnical
Conference.
Svanø, G. (1981). Undrained effective stress analysis. NTH Trondheim,
160 p.
Tavenas, F., Trak, B. & Leroueil, S. (1980). Remarks on the validity of
stability analyses. Canadian Geo-
technical Journal 17, 61-73
Wheeler, S., Näätänen, A., Karstunen, M. & Lojander, M. (2003). An
anisotropic elastoplastic model for soft clays. Canadian
Geotechnical Journal 40, 403-418


