2858
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
iterative algorithm until they converge to a unique solution for a
given soil profile, pile geometry and applied loading.
4 RESULTS
To illustrate the use of the analysis, a 15-m long drilled shaft
with a diameter of 0.6 m and pile modulus
E
p
= 24 GPa,
embedded in a four-layer soil deposit with
H
1
= 2.0 m,
H
2
= 5.0
m, and
H
3
= 8.3 m;
E
s
1
= 20 MPa,
Es
2
= 35 MPa,
E
s
3
= 50 MPa
and
E
s
4
= 80 MPa;
s
1
= 0.35,
s
2
= 0.25,
s
3
= 0.2 and
s
4
= 0.15
is considered (
E
si
and
si
are the soil Young’s modulus and
Poisson’s ratio for the
i
th
layer). A horizontal force
F
a
= 300 kN
acts on the pile. The pile head and base are free to deflect and
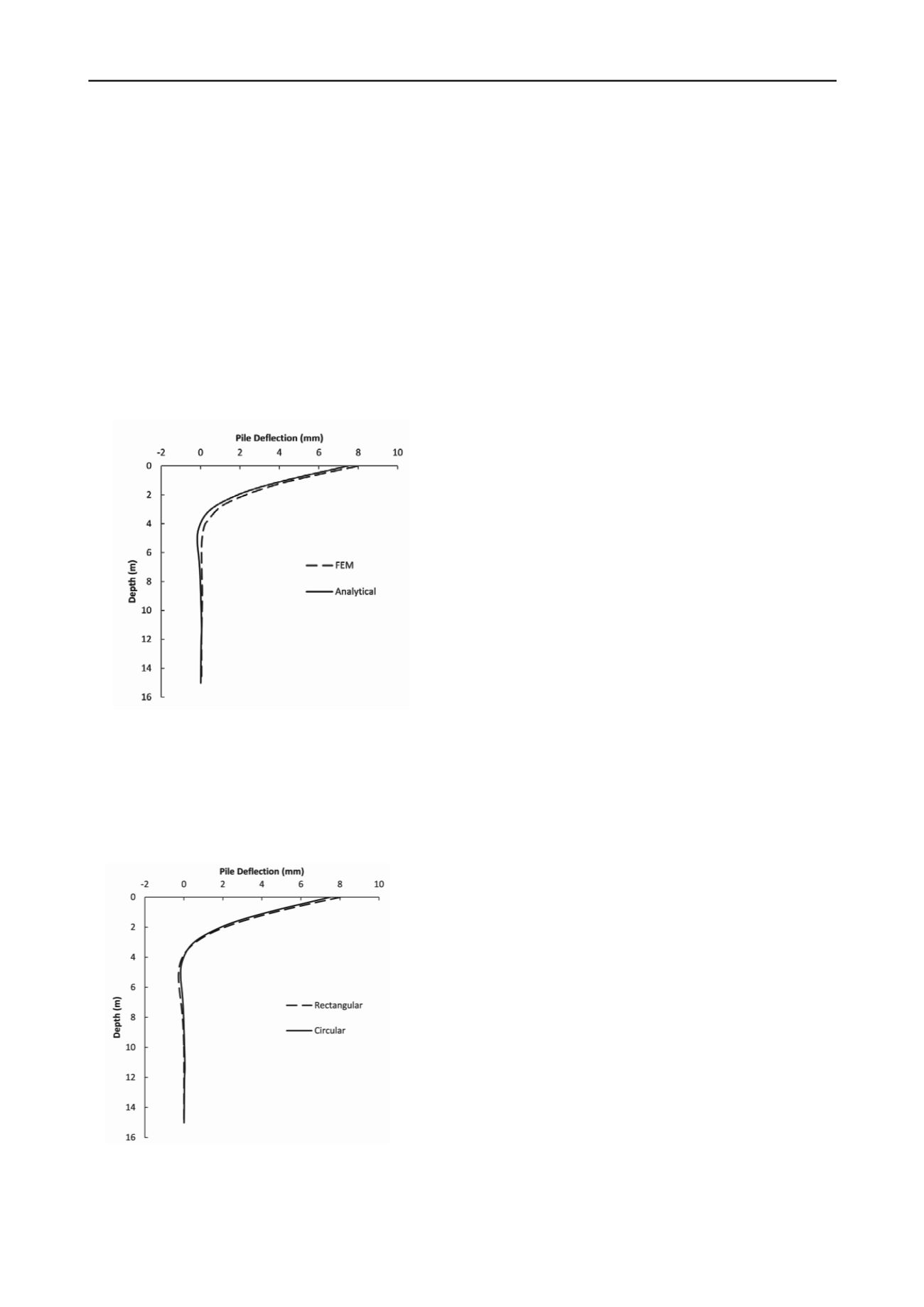
rotate. Figure 2 shows the pile deflection profile obtained using
the present analysis and an analysis performed using the 3D FE
method.
Figure 2. Deflection of a circular cross-section pile of 15 m length
As shown in Figure 2, the results match those of the FE
analysis closely. The difference in the head deflection obtained
from the present analysis and FE analysis is 6.6%.
Analyses were also performed on a square pile of 0.53m ×
0.53m (which has the same flexural rigidity as that of the
circular pile described above) embedded in the same soil profile
as of Figure 2. Figure 3 compares the response of the square
cross-section pile and the circular cross-section pile.
Figure 3. Deflection of a circular and rectangular cross-section piles of
15 m length and same flexural rigidity
Figure 3 shows that, if the second moment of inertia is the
same for the piles, they will have (approximately) the same
response under lateral loading even if the shapes of their cross
sections are different. So, in summary, rectangular piles can be
analyzed for lateral loads by replacing them with circular piles
having the same second moment of inertia. However, this would
work well for linear elastic soil in which knowledge of the
appropriate soil constants is presumed, but would not be
justified for an analysis that takes full account of soil non-
linearity in which knowledge of the operative values of the soil
‘constants’ is not available a priori and must be obtained from
the calculations themselves.
5 CONCLUSIONS
Analytical solutions for laterally loaded piles with rectangular
and circular cross sections embedded in multilayered elastic
media are obtained. The solutions produce the pile deflection,
slope of the deflected curve, bending moment and shear force as
functions of depth if the following are known: the pile cross-
sectional dimensions and length, thicknesses of the soil layers,
Young’s modulus of the pile material, the Young’s modulus and
Poisson’s ratio (or any pair of elastic constants) of the soils in
the various layers, and the magnitudes of the applied force and
moment. The governing differential equations for the pile
deflections are obtained using the principle of minimum
potential energy. The solution to all the governing differential
equations is obtained iteratively and depends on the rate at
which the displacements in the soil medium decreases with
increasing distance from the pile. The shape of the pile cross
section has a bearing on the pile response; however, it was
shown that the piles with the same second moment of inertia
produced the same response in elastic medium. The analysis
presented in the paper can be used to make realistic predictions
of the response of laterally loaded rectangular and circular piles.
6 REFERENCES
Anderson, J. B., Townsend, F. C. & Grajales, B. (2003). Case history
evaluation of laterally loaded piles.
J. Geotech. Geoenviron. Engng,
ASCE, 129( 3), 187–196.
Ashour M, Norris G. (2000). Modeling lateral soil–pile response based
on soil–pile interaction.
J. Geotech. Geoenviron. Engng
, ASCE,
126(5):420–428.
Basu D, Salgado R., Prezzi, M. (2009). A continuum-based model for
analysis of laterally loaded piles in layered soils,
Geotechnique
59(2), 127–140.
Basu D, Salgado R. (2008). Analysis of laterally loaded piles with
rectangular cross sections embedded in layered soil,
Int. J. Numer.
Anal. Meth. Geomech.
32:721–744.
Banerjee, P. K. & Davies, T. G. (1978). The behaviour of axially and
laterally loaded single piles embedded in nonhomogeneous soils.
Geotechnique
28(3), 309–326.
Cox WR, Reese LC, Grubbs BR. (1974). Field testing of laterally
loaded piles in sand.
Proceedings of the 6th Offshore Technology
Conference
, vol. 2, Houston, TX; 459–472.
Kim, B. T., Kim, N.-K., Lee, W. J. & Kim, Y. S. (2004). Experimental
load-transfer curves of laterally loaded piles in Nak-Dong river
sand.
J. Geotech. Geoenviron. Engng,
ASCE, 130(4), 416–425.
Poulos, H. G. (1971a). Behavior of laterally loaded piles: I – single
piles.
J. Soil Mech. Found. Div
. ASCE 97, No. SM5, 711–731.
Poulos, H. G. (1971b). Behavior of laterally loaded piles: III – socketed
piles.
J. Soil Mech. Found. Div
. ASCE 98, No. SM4, 341–360.
Randolph, M. F. (1981). The response of flexible piles to lateral
loading.
Geotechnique,
31(2), 247–259.
Reese LC, Cox WR. (1969). Soil behavior from analysis of tests of
uninstrumented piles under lateral loading.
Performance of Deep
Foundations
; 444:160–176.


