2867
Technical Committee 212 /
Comité technique 212
‐30
‐25
‐20
‐15
‐10
‐5
0
0
5
10
15
20
25
30
35
40
45
Displacement[mm]
GrossO‐cell load [MN]
Initial O‐cell downward
End of creep O‐cell down
Figure 11. Displacement of lower O-cell plate versus applied downward
gross O-cell load
0
0.5
1
1.5
2
2.5
0
5
10
15
20
25
30
35
40
45
D
isplacem
ent [m
m
]
GrossO‐cell load [MN]
Initial O‐cell upward
End of creepO‐cell up
Figure 12. Displacement of upper O-cell plate versus applied upward
gross O-cell load
Considering, that the major part of the load below the O-cells is
taken by toe bearing the creep rate is acceptably low. The corre-
sponding creep rates for the top plate of the O-cells are an order
of magnitude smaller and hence insignificant.
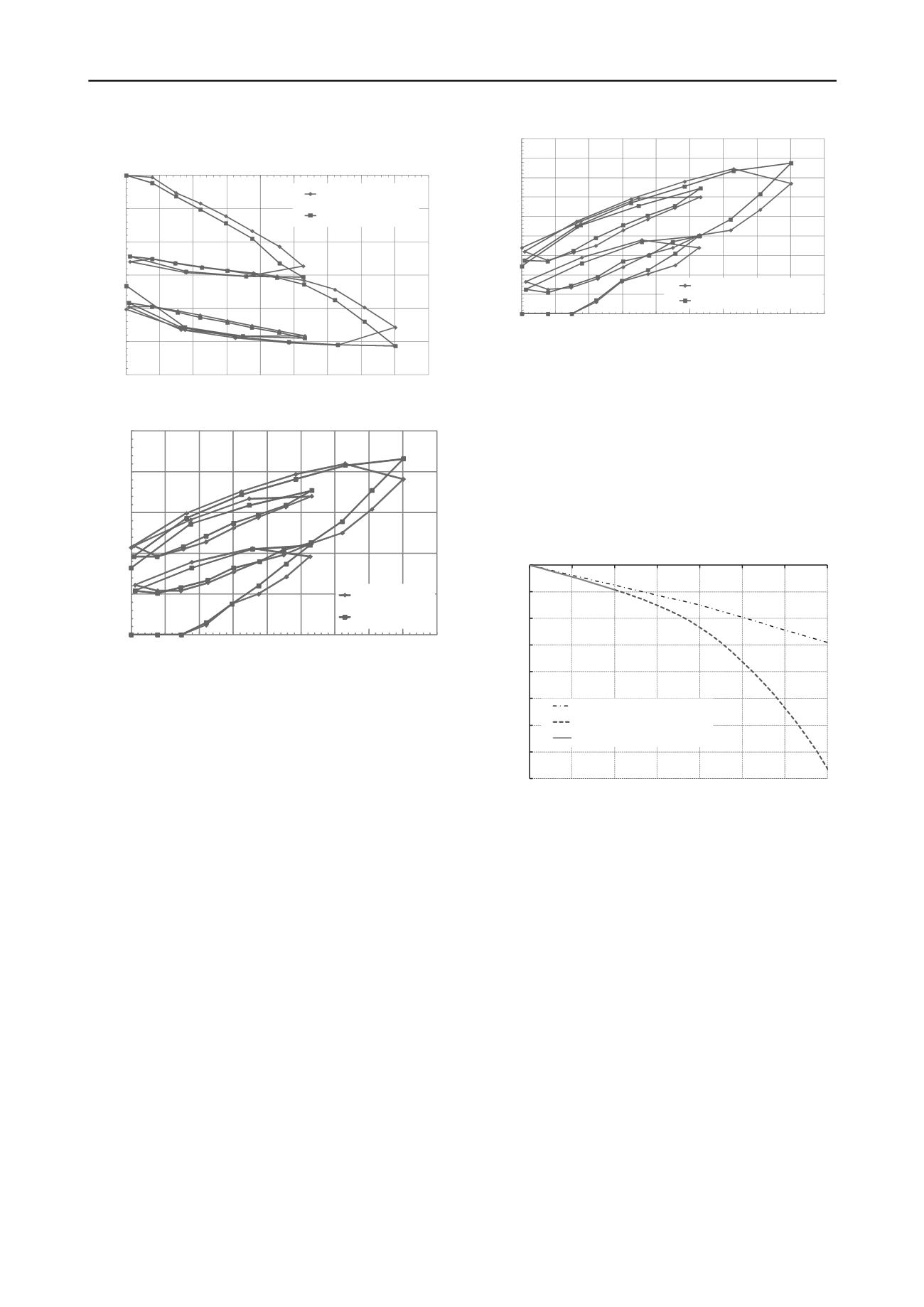
The load-displacement curve for the upward O-cell dis-
placement is shown in Figure 12. The upwards displacements
are significantly less than the downward displacements (Figure
11) and they are only initiated at an O-cell load of 7 MN after
which the load-displacement curve is essentially linear. It is ap-
parent that shaft stresses are locked into the system at unloading
resulting in a non-recoverable displacement of approximately 1
mm after unloading from the gross O-cell load of 40.1 MN (net
load 38.8 MN after subtraction of pile weight).
From the readings of tell tales 2 and 3 it is apparent that the
displacements decrease very significantly with the distance
from the O-cells and that initiation of displacements requires
significantly greater O-cell loads than needed to initiate down-
ward displacement.
Tell tales 2 are at the transition from Marlstone to Marl 2 and
hence the difference between tell tales 1 (top of O-cells) and 2
indicate the "rock socket" shortening in the Marlstone as shown
in Figure 13.
This deformation corresponds to the accumulated displace-
ment between pile and rock for developing the shaft resistance.
As seen from the Figure the displacement is very small and al-
most mirrors the upward displacement of the O-cell upper plate
(Figure 11). It means that the displacement between pile and
rock at the top of the Marlstone is only 0.6 mm and thus the pile
capacity is very significantly higher.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
0
5
10
15
20
25
30
35
40
45
Displacement[mm]
GrossO‐cell load [MN]
Marlstone shortening initial
Marlstone shortening end creep
Figure 13. Shortening of the pile ("rock socket") in Marlstone between
tell tales 1 and 2 versus applied O-cell gross load.
The recorded working curves for the upper pile shaft and the
lower pile segment may be fitted by "linear fractional" (hyper-
bolic) functions, i.e.
y = (ax + b)/(cx + d).
This facilitates ex-
trapolation of the working curves and production of synthesized
top load settlements curves.
The methodology by Fleming (1992) was used to produce
the predicted top load settlement curve shown in Figure 14.
0
10
20
30
40
50
60
70
80
0
20
40
60
80
100
120
140
Predicted pile top settlement [mm]
Pile head load [MN]
Elastic shortening
Total settlement
Predictedfrommeasuredvalues
Figure 14. Predicted top load settlement curve for Pile P4/3
It is apparent from Figure 14 that a top loading of 26.5 MN
(corresponding to the maximum SLS load in the P4 Pylon pile
group) will cause a pile head settlement in the order of 6 mm.
Twice the load, 53 MN (twice the SLS load and larger than the
maximum ULS load of 45.5 MN in the pile group) will result in
only 13 mm settlement.
Thus, even for the ultimate limit state (ULS-EQ) loading of
the actual pile of 29.6 MN the predicted settlements are only
slightly larger than the elastic part of the working curve.
6 EVALUATION OF ROCK SOCKET CAPACITY
The maximum toe and shaft design loads for pile P4/3 are 4.5 to
4.9 MN and 21.0 to 26.5 MN, respectively. The range reflects
upper and lower bound soil stratification and soil spring as-
sumptions. As seen from Figure 11 and Figure 12 the load test
indicates much higher values even within near elastic load-
displacement behaviour.
For the toe bearing of the rock socket the mobilisation of the
resistance may be assumed to vary roughly proportional to the
square root of the mobilised displacement, where
ult,t
(toe bear-
ing) ~ 0.1
D
= 200 mm:


