2726
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
It is also found that the empirical equation suggested by
Randolph (Equation 1) overpredicts the settlement ratio for
four-pile groups by 22% for
S
p
=
2D
and by 45% for
S
p
greater
than
3D
. In addition, using the equation proposed by Randolph
and Poulos (1982) to obtain the interaction factor,
α
v
, for helical
piles assuming straight shaft with diameter
D
for
S
p
=
2D
yields
largely overestimated interaction effect. On the other hand,
using a straight shaft pile diameter of
d
(i.e. helical pile shaft
diameter) yields comparable values to the ones obtained by the
parametric study.
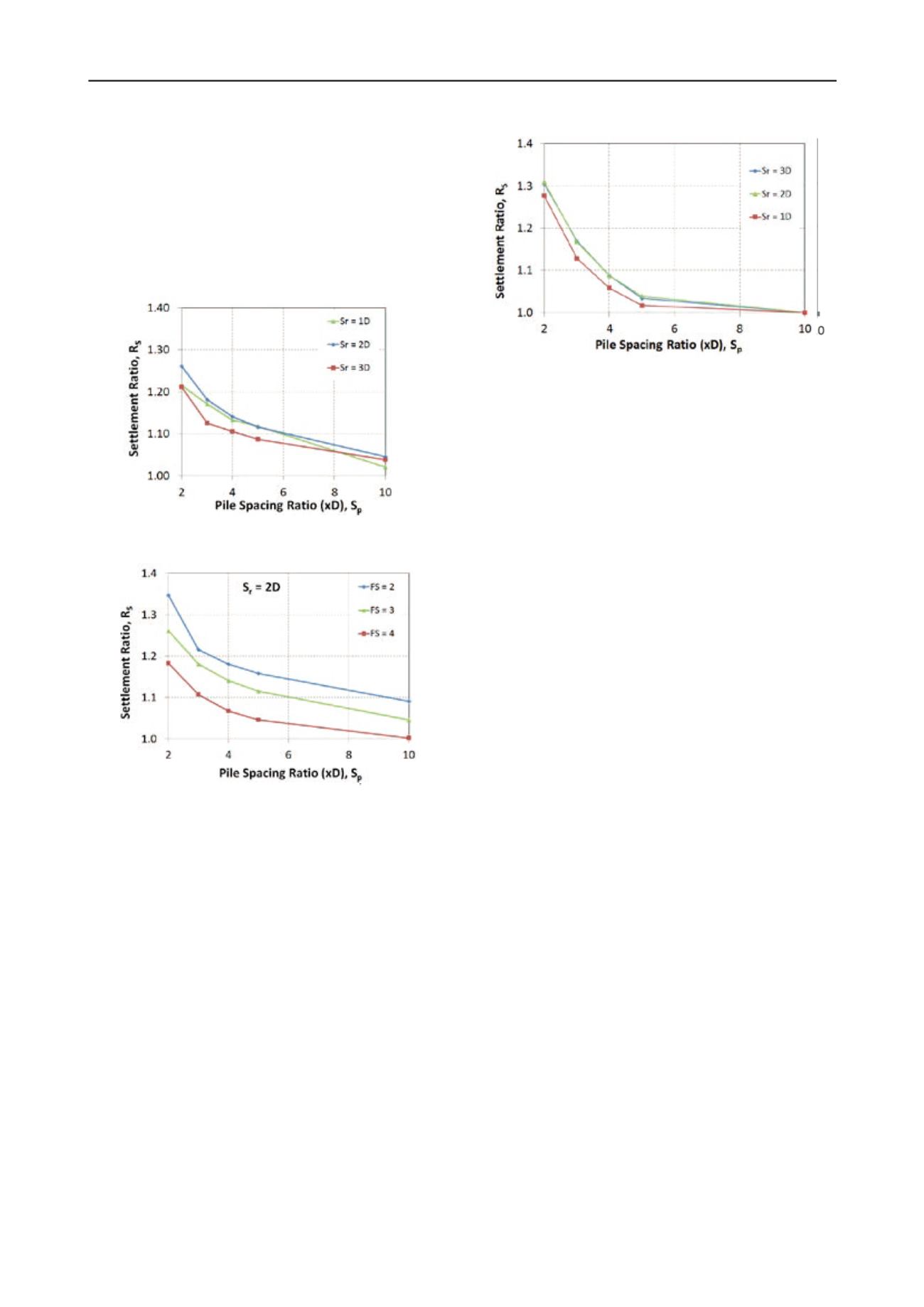
Figure 7. The settlement ratio for 4-piles group in clay with different
S
r
5 CONCLUSIONS
The performance of a helical pile group in sand or clay is
mainly affected by the piles center to center spacing. The
practical range of inter-helix spacing (
1D
to
3D
) has negligible
effect on
R
s
. The factor of safety,
FS
, could significantly affect
R
s
for piles in sand and has negligible effect for piles in clay. In
addition, the settlement ratio,
R
s
, for a pile group is not simply
an algebraic summation of the interaction factors,
α
ij
, of the
piles in the group.
Figure 5. The settlement ratio for 4-piles group in sand with different
S
r
Finally,
R
s
can be conservatively estimated using the
methods reported herein using a straight shaft pile with a
diameter equal to the shaft diameter of the helical pile. In
general,
R
s
for helical piles with multiple helices spaced at a
typical pile spacing of
3D
is in the range of 1.15 to 1.2 for both
clay and sand.
6 ACKNOWLEDGEMENT
The authors wish to extend their thanks to the National Science
and Engineering Research Council of Canada (NSERC) for the
generous financial support. The authors also extend their thanks
and appreciation to Helical Pier Systems (HPS) and Almita
Piling Inc. for their continuous support.
Figure 6. The effect of the factor of safety on the settlement ratio for 4-
piles group in sand
7 REFERENCES
For piles in clay, it is found that
R
s
could be as high as 1.33 for
S
p
=
2D
and as low as 1.1 for
S
p
=
3D
, as shown in Figure 7.
The settlement ratios are the highest at
S
p
=
2D
and decrease
rapidly with increasing spacing. It is also found that
S
r
has a
negligible effect on
R
s
.
ASTM. (2007).
Standard test methods for deep foundations under axial
compressive load, D1143M-07.
West Conshohocken: ASTM
International.
Similar to piles in sand, it is also found that
R
s
for a group of
piles is not a linear algebraic summation of the interaction
factors,
α
ij
, of the piles in the group. It is found that the
empirical equation suggested by Randolph (Equation 1) over-
predicts
R
s
by 80% for piles spaced at
2D
and by 100% for
S
p
greater than
3D
. In addition, using Poulos (1979) charts and
Randolph and Poulos (1982) equation, (Poulos, 1988), to obtain
α
v
assuming straight shaft piles diameter of
D
for
S
p
=
2D
is
found to overestimate
α
v
. On the other hand, using the same
charts and equation with a straight shaft pile diameter of
d
yields comparable values to the ones obtained by the parametric
study.
Basile, F. (1999). Non-linear analysis of pile groups.
Proceedings of the
Institution of Civil Engineers (UK), Geotechnical Engineering
,
137(2), 105-115.
CFEM. (2006).
Canadian Foundation Engineering Manual
(4th ed.).
Richmond, BC: BiTech Publishers Ltd.
Livneh, B., & El Naggar, M. H. (2008). Axial testing and numerical
modeling of square shaft helical piles under compressive and
tensile loading.
Canadian Geotechnical Journal
, 1142-1155.
Mitsch, M., & Clemence, S. (1985). The uplift capacity of helix anchors
in sand. In S. Clemence (Ed.),
Proceedings of the Uplift Behaviour
of Anchor Foundations in Soil
(pp. 26-47). Detroit: ASCE.
Narasimha Rao, S., Prasad, Y., & Shetty, M. (1991). The behaviour of
model screw piles in cohesive soils.
Journal of Soils and
Foundations, 31
, 35-50.
Poulos, H. (1988).
Marine Geotechnics.
London: Unwin Hyman Ltd.
Finally, in contrast to piles in sand, it is found that
R
s
at
service load considering
FS
= 2 is lower than
R
s
for service
loads given by
FS
= 4, however the effect is negligible.
Rowe, R. K. (2001).
Geotechnical and geoenvironmental engineering
handbook.
Massachusetts: Kluwer Academic Publishers.
Randolph, M.F. (1994). Design methods for pile groups and piled rafts.
Proc. 13
th
Int. Conf. S.M. & Found. Eng.,
5: 61-82
Int. Conf. S.M. & Found. Eng., 5: 61-82.
SIMULIA. (2009).
Getting Started with ABAQUS: Interactive Edition.
Providence: Dassault Systèmes Simulia Corp.
Zhang, D. J. (1999).
Predicting Capacity of Helical Screw Piles in
Alberta Soils. Unpublished master's thesis
. Alberta, Canada:
University of Alberta.
Figure 5. The settlement ratio for 4-piles group in sand with different
S
r
Figure 6. The effect of the factor of safety on the settlement ratio for 4-
piles group in sand
For piles in clay, it is found that
R
s
could be as high as 1.33 for
S
p
=
2D
and as low as 1.1 for
S
p
=
3D
, as shown in Figure 7. The
settlement ratios are the highest at
S
p
=
2D
and decrease
rapidly with increasing spacing. It is also found that
S
r
has a
negligible effect on
R
s
.
Similar to piles in sand, it is also found that
R
s
for a group of
piles is not a linear algebraic summation of the interaction
factors,
α
ij
, of the piles in the group. It is found that the
empirical equation suggested by Randolph (Equation 1) over-
predicts
R
s
by 80% for piles spaced at
2D
and by 100% for
S
p
greater than
3D
. In addition, using Poulos (1979) charts and
Randolph and Poulos (1982) equation, (Poulos, 1988), to obtain
α
v
assuming straight shaft piles diameter of
D
for
S
p
=
2D
is
f und to overestimate
α
v
. On the other hand, us ng the same
charts and equation with a straight shaft pile diameter of
d
yields comparable values to the ones obtained by the
parametric study.
Finally, in contrast to piles in sand, it is found that
R
s
at
service load considering
FS
= 2 is lower than
R
s
for service loads
given by
FS
= 4, however the effect is negligible.
Figure 7. The settlement ratio for 4-piles group in clay with different
S
r
5
CONCLUSIONS
The performance of a helical pile group in sand or clay is mainly
affected by the piles center to center spacing. The practical
range of inter-helix spacing (
1D
to
3D
) has negligible effect on
R
s
. The factor of safety,
FS
, could significantly affect
R
s
for piles
in sand and has negligible effect for piles in clay. In addition,
the settlement ratio,
R
s
, for a pile group is not simply an
algebraic summation of the interaction factors,
α
ij
, of the piles
in the group.
Finally,
R
s
can be conservatively estimated using the
methods reported herein using a straight shaft pile with a
diameter equal to the shaft diameter of the helical pile. In
general,
R
s
for helical piles with multiple helices spaced at a
typical pile spacing of
3D
is in the range of 1.15 to 1.2 for both
clay and sand.
6
ACKNOWLEDGEMENT
The authors wish to extend their thanks to the National Science
and Engineering Research Council of Canada (NSERC) for the
generous financial support. The authors also extend their
thanks and appreciation to Helical Pier Systems (HPS) and
Almita Piling Inc. for their continuous support.
7
REFERENCES
ASTM. (2007).
Standard test methods for deep foundations under axial
compressive load, D1143M-07.
West Conshohocken: ASTM
International.
Basile, F. (1999). Non-linear analysis of pile groups.
Proceedings of the
Institution of Civil Engineers (UK), Geotechnical Engineering
,
137(2), 105-115.
CFEM. (2006).
Canadian Foundation Engineering Manual
(4th ed.).
Richmond, BC: BiTech Publishers Ltd.
Livneh, B., & El Naggar, M. H. (2008). Axial testing and numerical
modeling of square shaft helical piles under compressive and
tensile loading.
Canadian Geotechnical Journal
, 1142-1155.
Mitsch, M., & Clemence, S. (1985). The uplift capacity of helix anchors
Figure 5. The settlement ratio for 4-piles group in sand with different
S
r
Figure 6. The effect of the factor of safety on the settlement ratio for 4-
piles group in sand
For piles in clay, it is found that
R
s
could be as high as 1.33 for
S
p
=
2D
and as low as 1.1 for
S
p
=
3D
, as shown in Figure 7. The
settlement ratios are the highest at
S
p
=
2D
and decrease
rapidly with increasing spacing. It is also found that
S
r
has a
negligible effect on
R
s
.
Similar to piles in sand, it is also found that
R
s
for a group of
piles is not a linear algebraic summation of the interaction
fac o s,
α
ij
, of the piles in the group. It is found tha the
empirical equation suggested by Ra dolph (Equation 1) ver-
predicts
R
s
by 80% for piles spaced at
2D
and by 100% for
S
p
greater than
3D
. In addition, using Poulos (1979) charts and
Randolph and Poulos (1982) equation, (Poulos, 1988), to obtain
α
v
assuming straight shaft piles diameter of
D
for
S
p
=
2D
is
found to overestimate
α
v
. On the other hand, usi g t e same
charts and equation with a straight shaft pile diameter of
d
yields comparable values to the ones obtained by the
parametric study.
Finally, in contrast to piles in sand, it is found that
R
s
at
service load considering
FS
= 2 is lower than
R
s
for service loads
given by
FS
= 4, however the effect is negligible.
Figure 7. The settlement ratio for 4-piles group in clay with different
S
r
5
CONCLUSIONS
The performance of a lical pile group in sand or clay is mainly
affected by the piles center to center spacing. T practical
range of inter-helix spacing (
1D
to
3D
) has negligible effect on
R
s
. The factor of safety,
FS
, could significantly affect
R
s
for piles
in sand and has negligible effect for piles in clay. In addition,
the settlement ratio,
R
s
, for a pile group is not simply an
algebraic summation of the interaction factors,
α
ij
, of the piles
in the group.
Finally,
R
s
can be conservatively estimated using the
methods ported herein using a straight haft pile with a
diameter equal to the shaft diameter of the helical pile. In
general,
R
s
for helical piles with multiple helices spaced at a
typical pile spacing of
3D
is in the range of 1.15 to 1.2 for both
clay and sand.
6
ACKNOWLEDGEMENT
The authors wish to extend their thanks to the National Science
and ngineering Research Council of Canada (NSERC) for the
generous financial support. The authors also extend their
thanks and appreciation to Helical Pier Systems (HPS) and
Almita Pil ng Inc. for their co tinuous support.
7
REFERENCES
ASTM. (2007).
Standard test methods for deep foundations under axial
compressive load, D1143M-07.
West Conshohocken: ASTM
International.
Basile, F. (1999). Non-linear analysis of pile groups.
Proceedings of the
I stitution of Civil Engineers (UK), Geotechnical Engineeri g
,
137(2), 105-115.
CFE . ( 006).
Canadian Foundation Engineering Manual
(4th ed.).
Richmond, BC: BiTech Publishers Ltd.
Livneh, B., & El Naggar, M. H. (2008). Axial testing and numerical
modeling of square shaft helical piles under compressive and
tensile loading.
Canadian Geotechnical Journal
, 1142-1155.
Mitsch, M., & Clemence, S. (1985). The uplift capacity of helix anchors
in sand. In S. Clemence (Ed.),
Proceedings of the Uplift Behaviour of
Anchor Foundations in Soil
(pp. 26-47). Detroit: ASCE.
Figure 5. The settlement ratio for 4-piles group in sand with different
S
r
Figure 6. The effect of the factor of safety on the settlement ratio for 4-
piles group in sand
For piles in clay, it is found that
R
s
could be as high as 1.33 for
S
p
=
2D
and as low as 1.1 for
S
p
=
3D
, as shown in Figure 7. The
settlement ratios are the highest at
S
p
=
2D
and decrease
rapidly with increasing spacing. It is also found that
S
r
has a
negligibl
t on
R
s
.
Similar to piles in sand, it is also found that
R
s
for a group of
piles i
ot a l ne r algebraic summation of t e interaction
factors,
α
ij
, of he piles in the group. It is fou that th
empirical equation sugg sted by Randolph (Equation 1) over-
redicts
R
s
by 80% for iles spaced t
2D
a by 100% for
S
p
greater than
3D
. In addition, using Poulos (1979) charts and
Randolph and Poulos (1982) equation, (Poulos, 1988), to obtain
α
v
assuming straight shaft piles diameter of
D
for
S
p
=
2D
is
found to overestimate
α
v
. On the other h , using the same
charts and equation with a straight shaft pile diameter of
yields comparable values to the ones obtained by the
parametric study.
Finally, in contrast to piles in sand, it is found that
R
s
at
service load considering
FS
= 2 is low r than
R
s
for service loads
give b
FS
= 4, how ver the eff ct is neglig ble.
Figure 7. The settlement ratio for 4-piles group in clay with different
S
r
5
CONCLUSIONS
The performance of a helical pile group in sand or clay is mainly
affected by the piles center to ce ter spacing. The practical
range of inter-helix spacing (
1D
to
3D
) has negligible effect on
R
s
. The factor of safety,
FS
, could significantly affect
R
s
for piles
in sand and has negligible effect for piles in clay. In addition,
the settlement ratio,
R
s
, for a pile group is not simply an
algebraic summatio of the interaction factors,
α
ij
, of the piles
in the group.
Finally,
R
s
can be conservatively estimated using the
methods reported herein using a straight shaf pile with a
di meter equal to the sha t diameter of the helic l pile. In
g n ra ,
R
s
for helical piles with multiple helices spaced t a
typic l pile spacing of
3D
is in the range of 1.15 to 1.2 for both
clay and sand.
6
ACKNOWLEDGEMENT
The authors wish to extend their thanks to the National Science
and Engineering Research Council of Canada (NSERC) for the
generous financial support. The authors also extend their
thanks and appreciation to Helical Pier Systems (HPS) and
Almita Piling Inc. for their continuous support.
7
REFERENCES
ASTM. (20 7).
Stand r test methods f r deep fou datio s under axial
compressive load, D1143M-07.
We t Conshohocken: ASTM
Internationa .
Basile, F. (1999). Non-linear analysis of pile groups.
Proceedings of the
Institution of Civil Engineers (UK), Geotechnical Engineering
,
137(2), 105-115.
CFEM. (2006).
Canadian Foundation Engineering Manual
(4th ed.).
Richmond, BC: BiTech Publi h r Ltd
Livneh, B., & El Naggar, M. H. (2008). Axial testing and numerical
modeling of square shaft helical piles under c mpressiv and
tensile loading.
Canadian Geotechnical Journal
, 1142-1155.
Mitsch, M., & Clemence, S. (1985). The uplift capacity of helix anchors
in sand. In S. Clemence (Ed.),
Proceedings of the Uplift Behaviour of
Anchor Foundations i Soil
(pp. 26-47). Detroit: ASCE.


