3400
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
1982): conductivity, convective transfer (convection), the
processes of evaporation and condensation (latent heat transfer),
heat radiation, ion exchange, freezing – thawing processes.
If the size of soil particles and pores is significantly small in
relation to the total soil, the complex process of heat transfer in
the ground can be reduced only to conductivity, which
dominates in the case of energy foundations.
If there is an internal heat source (internal heat generation) in
the concerned ground quantity, the basic equation of heat
conductivity is as follows:
c
q
t
t
(1)
where, α is thermal diffusivity,
t
is Laplace operator,
is
power of internal heat sources, t is temperature,
is time,
c
is
specific thermal capacity and
ρ
is density of solid medium.
q
Differential equations of heat conductivity show a character
of the process and have many solutions. To obtain the solution
of a specific task it is necessary to have initial and boundary
conditions. Because of mathematical difficulties, the analytical
solutions of these equations are possible only for simple cases.
At present, a number of software packages that solve the
problem of heat transfer in soils, including calculations of
energy foundations have been developed.
3 EXPERIMENTAL INVESTIGATIONS
Field studies of ground were carried out at a specially chosen
pilot site to determine temperature distribution in the ground
mass, change of ground-water level and physical-mechanical
and thermal-physical characteristics of the ground mass.
Engineering and geological structure of the site was defined
by the results of the research done. Geologically, the
experimental platform is composed of Quaternary alluvial-
diluvial clay soils, at the base with pebbles up to 60-70 % of the
total thickness of 11.6 m, overlapped by the thickness of filled-
up ground of 6.0m thick. Bedrock is argillites, uncovered at a
depth of 17.6 m.
The following physical-mechanical and thermal-physical
characteristics of the experimental site ground were obtained on
the results of laboratory work:
Table 1. Characteristics of the experimental site ground
№
Soil
classification
Deep
(m)
(t/m
3
)
w
e
c
(kJ/
kg°C)
(W/
m°С
)
1 Filled-up
ground
0-6
1.91
0.25 0.73
1.27
1.33
2 Low
plasticity
loam
6-13 1.92
0.22 0.8
1.25
1.21
3 Gravel
ground
13-
17.6
1.69
0.007
0.85
0.41
4 Heavily
weathered,
cracked and
waterlogged
argillite
17.6
2.27
0.1 0.31
1.07
0.59
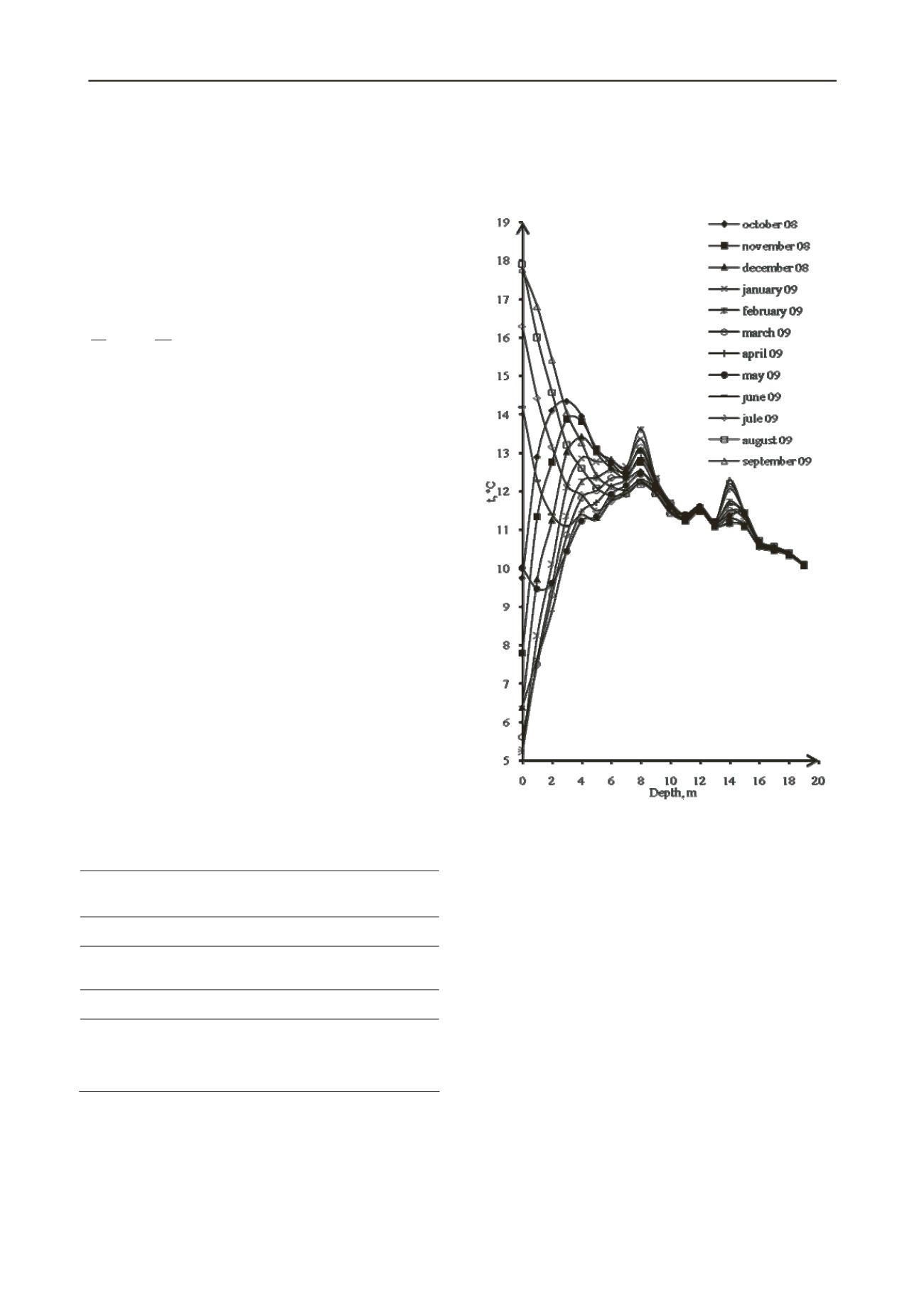
The diagrams of depth temperature distribution in the ground
and its seasonal variations were obtained on the results of
monitoring (Fig.1). Temperature fluctuations in the ground
mass starting from the depth of 6.0 m are negligible. The
maximum deviation from the mean temperature is less than
0.24°C. The temperature of the ground mass deeper than the
depth of 6.0 m varies from 13° to 10° C, gradually decreasing
with depth, being equal to 12°C before the depth of 12.0 m,
11°C from the depth of 10m to 16m and 10°C at the depth of
more than 16m.
Positive surface temperature of the soil caused by the
construction of overall housing for the recording equipment.
Figure 1. Diagram of depth distribution of temperature in the ground
mass.
On the results of groundwater level monitoring it was
established that the average groundwater level was 2.55 m.
Groundwater level variations with time are negligible.
To carry out numerical simulation, software-complex
GeoStudio was selected. Its basic differential equation is the
fundamental heat conduction equation with an internal heat
source (Grigorjev V.A. et al. 1982).
Test problems for three main types of underground structures
being in contact with ground were preliminary solved:
- a pile with a diameter of 1.2m and 20m long;
- a 24m wide slab foundation, the depth of foundation is
20m;
- a slurry wall of 20m deep.
The temperature at each node in the initial period of time
was taken as initial conditions. Boundary conditions were
specified for the ground surface and for the lower boundary of
the model. The boundary conditions of the lower boundary were
taken as time-constant value of the heat flow density. The
boundary conditions for the surface were set by applying
climatic characteristics in the city of Perm in 2009.
Time parameters of the simulation (number of annual cycles)
were taken on the condition of setting a “new” temperature
regime of the ground mass taking into account the thermal
energy that was extracted.


