3408
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
des températures mesurées dans des pieux géothermiques
instrumentés justifie cette approche (Bourne-Webb
et al.
2009).
Cette variation est intégrée dans le calcul en retenant une valeur
du coefficient de dilatation thermique du béton
α
T
égale à
1,2x10
-5
°C
-1
et en imposant une déformation axiale. Seul le
premier chargement thermique est considéré si bien que les
éventuels effets cycliques ne peuvent pas être pris en compte.
Le sol situé autour du pieu est supposé ne pas être soumis à des
variations volumiques d’origine thermique, ce qui est valable
quand l’écoulement de la nappe est suffisant (supérieur à 10
cm/jour) pour maintenir la température du sol constante
(Fromentin
et al.
1999).
Trois types de conditions en tête de pieu sont possibles : (i)
pieu libre en tête (l’effort en tête de pieu n’est pas modifié lors
de l’application du chargement thermique), (ii) pieu bloqué en
tête (le déplacement en tête de pieu n’est pas modifié lors de
l’application du chargement thermique) et (iii) prise en compte
d’une rigidité en tête de pieu modélisant les conditions de
liaison de ce dernier avec la structure portée.
2.3 Résultats obtenus
La méthode de calcul permet d’obtenir l’évolution des
contraintes normales
n
, des déplacements verticaux w et de la
mobilisation du frottement axial q
s
avec la profondeur. Les
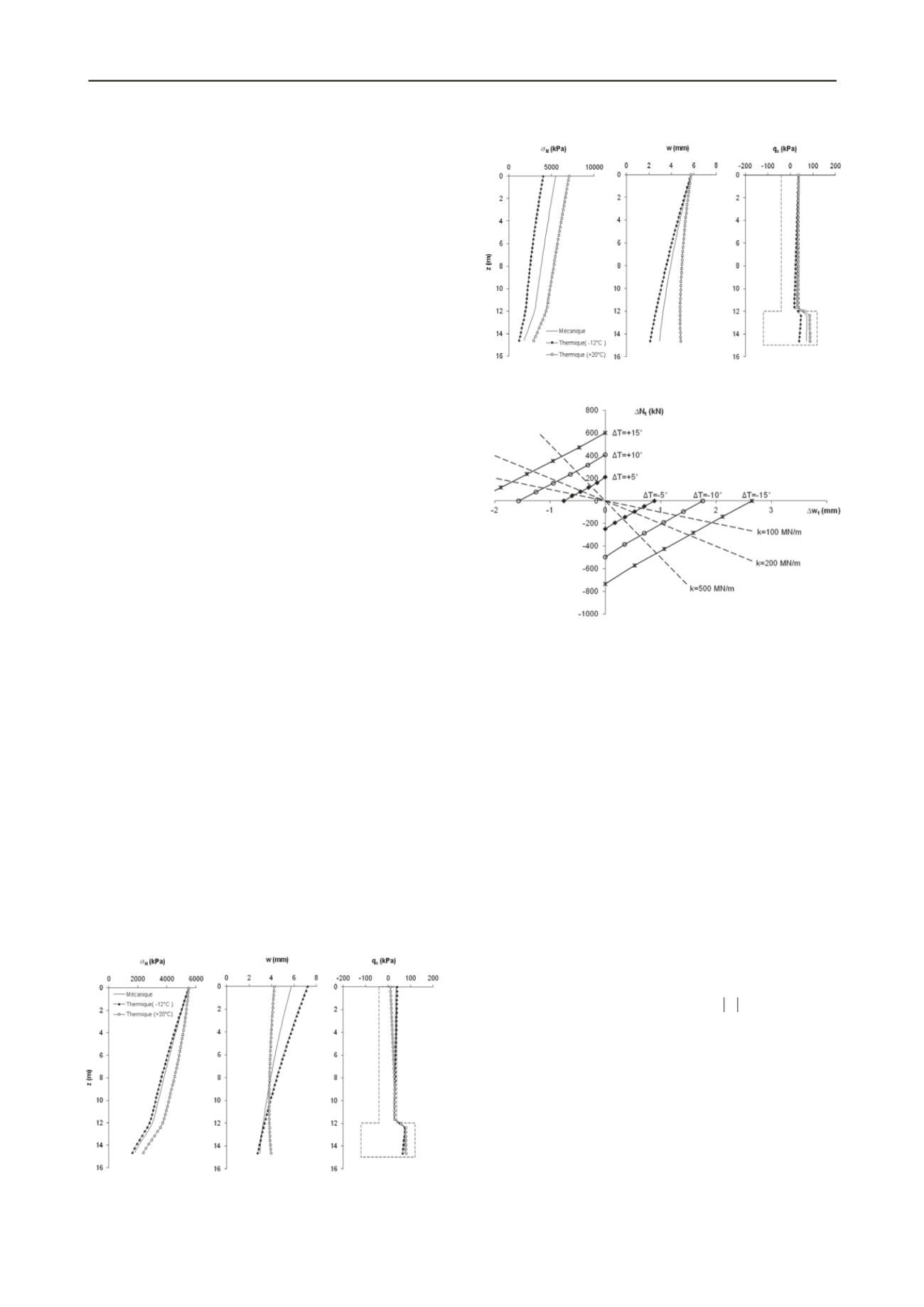
figures 1 et 2 présentent les « résultats-types » obtenus pour un
pieu respectivement libre et bloqué en tête : par rapport à la
situation où le pieu est simplement chargé mécaniquement, la
déformation appliquée en hiver correspond à une diminution de
la température de 12°C et celle appliquée en été à une
augmentation de 20°C.
Ces comportements extrêmes permettent d’appréhender le
comportement réel d’un pieu géothermique pour lequel la
rigidité en tête est intermédiaire. Pour un pieu libre en tête, le
refroidissement de ce dernier induit un tassement
supplémentaire ainsi qu’une diminution de la contrainte
normale dans les sections du pieu, voire dans certains cas,
l’apparition de traction. Le réchauffement de la fondation
conduit à un soulèvement de la tête de pieu accompagné d’une
augmentation de la contrainte normale dans les sections du pieu.
Dans tous les cas, les variations de température sont associées à
des modifications de la répartition du frottement axial. Pour un
pieu bloqué en tête, les résultats peuvent être interprétés de
manière similaire.
2.4 Abaque de représentation du comportement global d’un
pieu géothermique
Cet abaque (Figure 3) permet d’appréhender simplement les
variations de déplacement vertical
w
t
et d’effort normal
Nt
en
tête de pieu lors de l’application du chargement thermique, pour
différentes gammes de température et de rigidité de la structure
portée (Habert et Burlon 2012).
Figure 1. Comportement d’un pieu « libre en tête »
Figure 2. Comportement d’un « pieu bloqué en tête »
Figure 3. Abaque global de fonctionnement d’un pieu géothermique
3 PRISE EN COMPTE DES EFFETS CYCLIQUES
3.1 Introduction
La répétition des dilatations et des contractions du pieu sous
l’effet des variations de température conduit à modifier plus ou
moins significativement la répartition du frottement axial et de
la contrainte à la base du pieu. Ces cycles sont alors susceptibles
de provoquer des dégradations du sol et de l’interface sol-pieu
et diverses stratégies de calcul peuvent être alors envisagées.
3.1.1 Modèle unidimensionnel : loi t-z cyclique
La loi
t-z
cyclique proposée est une loi d’interaction locale
fondée sur les mêmes principes que la loi de Frank et Zhao
(Frank et Zhao 1982, Suryatriyastuti
et al.
2012). Elle permet de
décrire de manière exhaustive chaque cycle de charge et de
décharge. Elle est définie par l’équation (3) où
n
désigne le
nombre de cycle de chargement,
q
si
[kPa] désigne le frottement
mobilisé à l’inversion de charge (
q
si
=0 pour
n
=1),
u
ti
[m] et
u
ts
[m] désignent respectivement le déplacement de l’interface sol-
pieu au cycle précédent (
u
ti
=0 pour
n
=1) et la somme des
valeurs absolues des déplacements (
).
q
sULT
[kPa] est
le frottement maximal axial mobilisable lors du premier cycle,
q
s
[kPa] et
[m] sont respectivement la variation positive ou
négative du frottement maximal mobilisable et la vitesse de
cette variation, et
[m] quantifie la rigidité de l’interface.
Les paramètres
A
et
R
(équations 4 et 5) permettent, à chaque
inversion de chargement, respectivement, de limiter la valeur de
frottement
q
s
et de quantifier l’éventuelle augmentation de
rigidité de l’interface au cours des cycles (le paramètre
définit
cette augmentation et le paramètre
indique la vitesse de cette
augmentation). La formulation de la loi
t-z
cyclique permet de
rendre compte des principaux phénomènes caractéristiques des
effets cycliques (Lemaitre et Chaboche 2009) : relaxation et
rochet.
ti
u
u
ts


