3394
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
0
0.02
0.04
0.06
Axial strain (zero before freezing)
0
1
2
3
q
[MPa]
-10
o
C
-5
o
C
-2
o
C
-1
o
C
-5
-4
-3
-2
-1
0
1
p
n
[MPa]
0
1
2
3
q
[MPa]
-10
o
C
-5
o
C
-2
o
C
-1
o
C
-5
-4
-3
-2
-1
0
1
p
n
[MPa]
0
5
10
15
s
[MPa]
Yield Surface
CSL
-10
o
C
-5
o
C
-2
o
C
-1
o
C
E
= 50 MPa
= 0.3
p
no
*
= 0.15 MPa
M
= 1
-
= 0.1
k
= 0.33
= 0
r
= 0
Parameters
Parametersconcerningthe mechanical model
Young’smodulus:
E
= 50 MPa
Poisson’s ratio:
= 0.3
Parameters f ryieldandhardening
(seeNishimuraetal., 2009b):
p
no
*
= 0.15 MPa
M
= 1,
–
= 0.1
k
= 0.33,
= 0,
r
= 0
Figure 7. Example of model performance in triaxial compression at
different temperatures; see Nishimura et al (2009b).
heave for the two cases, confirming the model’s ability to
capture the field heaving behaviour. The values of input
parameters and the processes of their determination are
described by Nishimura et al. (2009b). The control case was
simulated with two different scenarios for the air temperature; it
was set either constant at +6.5
o
C, or varied monthly, oscillating
between +16.5
o
C in July and -8
o
C in January.
0
200
400
600
800
1000
Time [Days]
0
20
40
60
80
Heave of pipeline [cm]
Observed
Simulated
C
D
Berm constructed
D
C
G
G
Constant air temp.
Monthly varying air temp.
Figure 8. Computed and observed heaves of pipelines: Observation data
from Slusarchuk et al. (1978). The ‘G’ case is a gravel-matted case; see
the original literature for details.
(a) Const. temp.: Day 300
(b) Const. temp.: Day 1000
(c) Varying. temp.: Day 300
(d) Varying. temp.: Day 1000
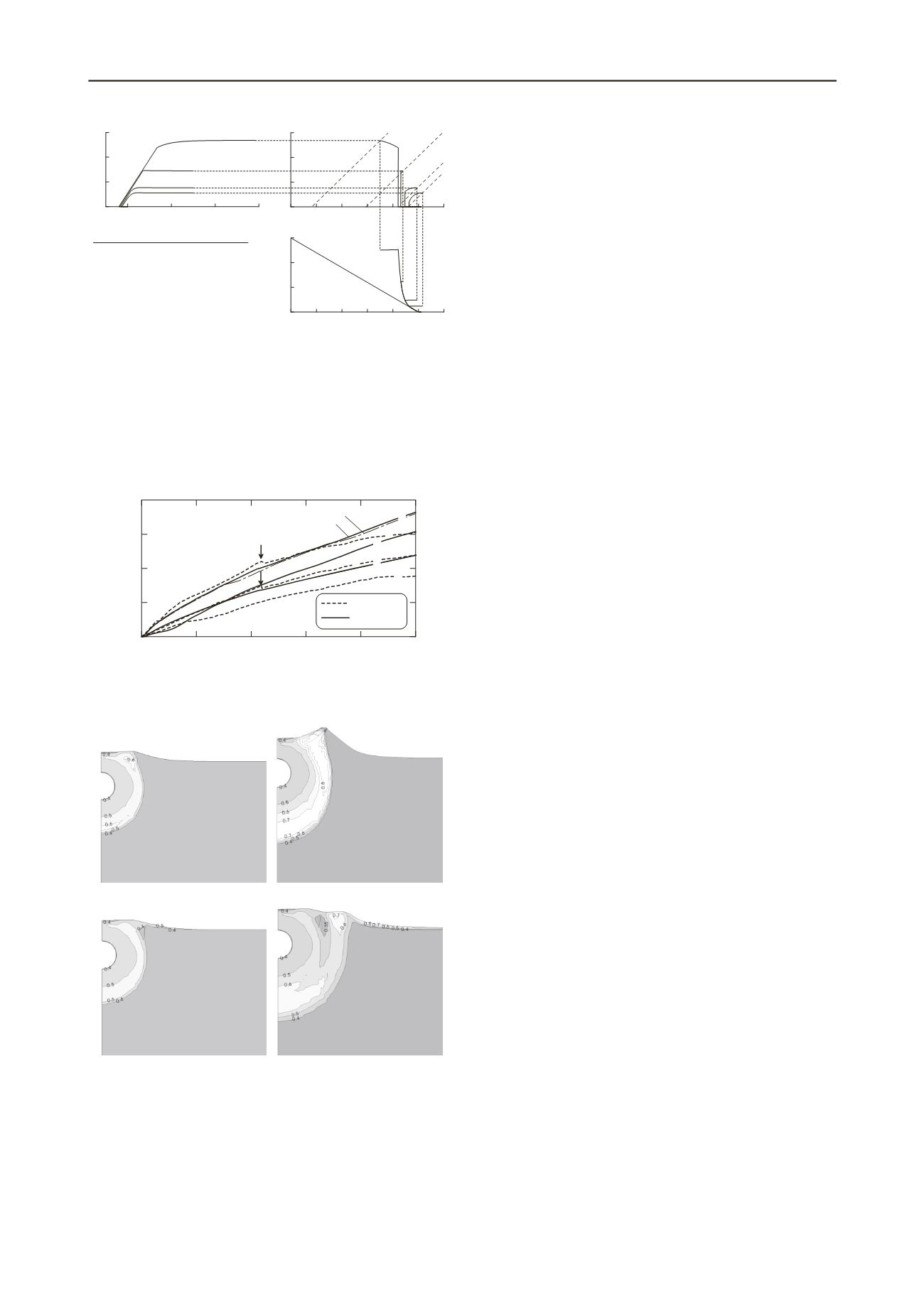
Figure 9. Computed geometry changes and porosity distributions.
The difference in the air temperature boundary conditions
affected the surface movement patterns, as shown in Figure 9,
despite the limited effect on overall pipe heave. Maintaining a
fixed temperature difference between the ground surface and the
chilled pipeline resulted in excessively large heave away from
the centreline and movements that could not be considered
reliably by the model’s small-strain formulation. In the case
with monthly variable ground surface temperature, surface
freezing during winter disrupted the frost heave and permitted a
more stable expansion of the frozen zones. The porosity
distribution shown in Figure 9 indicate highly dilated, ice-rich
areas around the pipeline, created by the influx of water drawn
in by the ‘suction’
P
l
-
P
i
,. The Calgary dataset allowed a critical
validation of the-THM model’s realistic performance. Inputting
longer-time, transient future local climatic/geothermal trends
from the middle-level analyses would allow the THM analyses
to predict the site-specific soil-structure response against
expected climate change.
5 CONCLUSIONS
A multiple-level analytical framework is proposed for
predicting soil-structure responses to climate change in those
cold regions where permafrost degradation plays an important
role. The framework places climate prediction at the highest
global level, and applies AOGCM data that is downscaled and
calibrated against local climate datasets. The next level
combines engineering geology with non-linear 1-D modelling to
generate extensive analytical databases from which regional
geocryological maps may be created that both inform hazard
mapping and strategic planning of extensive infrastructure. As
well as providing a middle-level screening tool, the geothermal
analysis can set the conditions for lower-level, site-specific
engineering analyses. A new THM-model with a novel
mechanical constitutive model has been proposed to help
predict the complex soil-structure interactions expected as
temperature changes encourage permafrost warming and
degradation. The mid-level approach was checked against
regional geothermal maps in Eastern Siberia, while the THM
analysis was tested against field tests on chilled pipelines in
Canada, confirming the predictions to be realistic in both cases.
6 ACKNOWLEDGEMENTS
The research described was funded by BP. Their support and
permission to publish the results is sincerely acknowledged.
7 REFERENCES
Alonso, E.E., Gens, A. and Josa, A. 1990. A constitutive model for
partially saturated soils.
Géotechnique
40 (3), 405-430.
Clarke, J., Fenton, J., Gens, A., Jardine, R., Martin, C., Nethercot, D.,
Nishimura, S., Olivella, S., Reifen, C., Rutter, P., Strasser, F. and
Toumi, R. 2008. A multi-disciplinary approach to assess the impact
of global climate change on infrastructure in cold regions,
Proc. 9th
Int. Conf. on Permafrost
, Fairbanks, 279-284.
Gens, A. 2010. Soil-environment interactions in geotechnical
Engineering. the 47th Rankine Lecture,
Géotechnique
60 (1) 3-74.
IPCC, 2007. Climate Change 2007: The physical science basis.
Contribution of Working Group I to the Fourth Assessment Report
of the Intergovernmental Panel on Climate Change, Cambridge
University Press.
Lunardini, V.J. 1978. Theory of n-factors and correlation of data.
Proc.
3rd Int. Conf. on Permafrost
, Edmonton, 41-46.
Nishimura, S. Martin, C.J., Jardine, R.J. and Fenton, C.H. 2009a. A new
approach for assessing geothermal response to climate change in
permafrost regions.
Géotechnique
59 (3), 213-227.
Nishimura, S., Gens, A., Olivella, S. and Jardine, R.J. 2009b. THM-
coupled finite element analysis of frozen soil: formulation and
application.
Géotechnique
59 (3), 159-171.
Slusarchuk, W.A., Clark, J.I., Nixon, J.F., Morgenstern, N.R. and
Gaskin, P.N. 1978. Field test results of a chilled pipeline buried in
unfrozen ground.
Proc. 3rd Int. Conf. on Permafrost
, Edmonton,
878-883.


