2800
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
carried out a series of numerical analyses and proposed the
following equation:
,
,
PR UR UR ult
PG u
Q
Q Q
lt
(1)
PR
Q
,
and
UR
Q
PG
Q
are the ultimate bearing capacities of the PR,
the isolated raft and the isolated pile respectively;
UR
is a
coefficient introduced to affect the raft bearing capacity when it
is considered to be working in the pile-raft system.
Numerical models were generated inducing settlements of 10%
of the raft width, which are considered to be capable of
mobilizing all the strength capacity of the system. The results
were used to make out a numerical correlation to obtain the
relation between
UR
and the geometry of the PR, which led to
the following expression:
1 3
G
UR
A s
A d
(2)
where
G
A
is the area enclosed by the piles;
A
is the raft area;
s
and are the pile spacing and diameter respectively.
d
3 APPLICATION OF THE LIMITE STATE METHOD
(LEM) TO THE PILED RAFT FOUNDATION DESIGN
The application of the Limit State Method (LEM) to the PR
design to be described in this article is based on a design in
which the piles behave as floating piles under ultimate or
limiting capacity. It is one of the options that generate the
greatest efficiency of the system, because it considers the piles
working at their ultimate creep stages (Randolph 1994). This
forces an analysis of the PR rather as a system than as
independent elements, since the piles will be working at their
ultimate stages and will consequently not satisfy any of the
safety criteria established in pile design codes. Off course this
obliges the contribution of the raft into design. Also, the safety
coefficient of the mechanical characteristics of the soil can be
applied to the mean values, as suggested by Quevedo (2002).
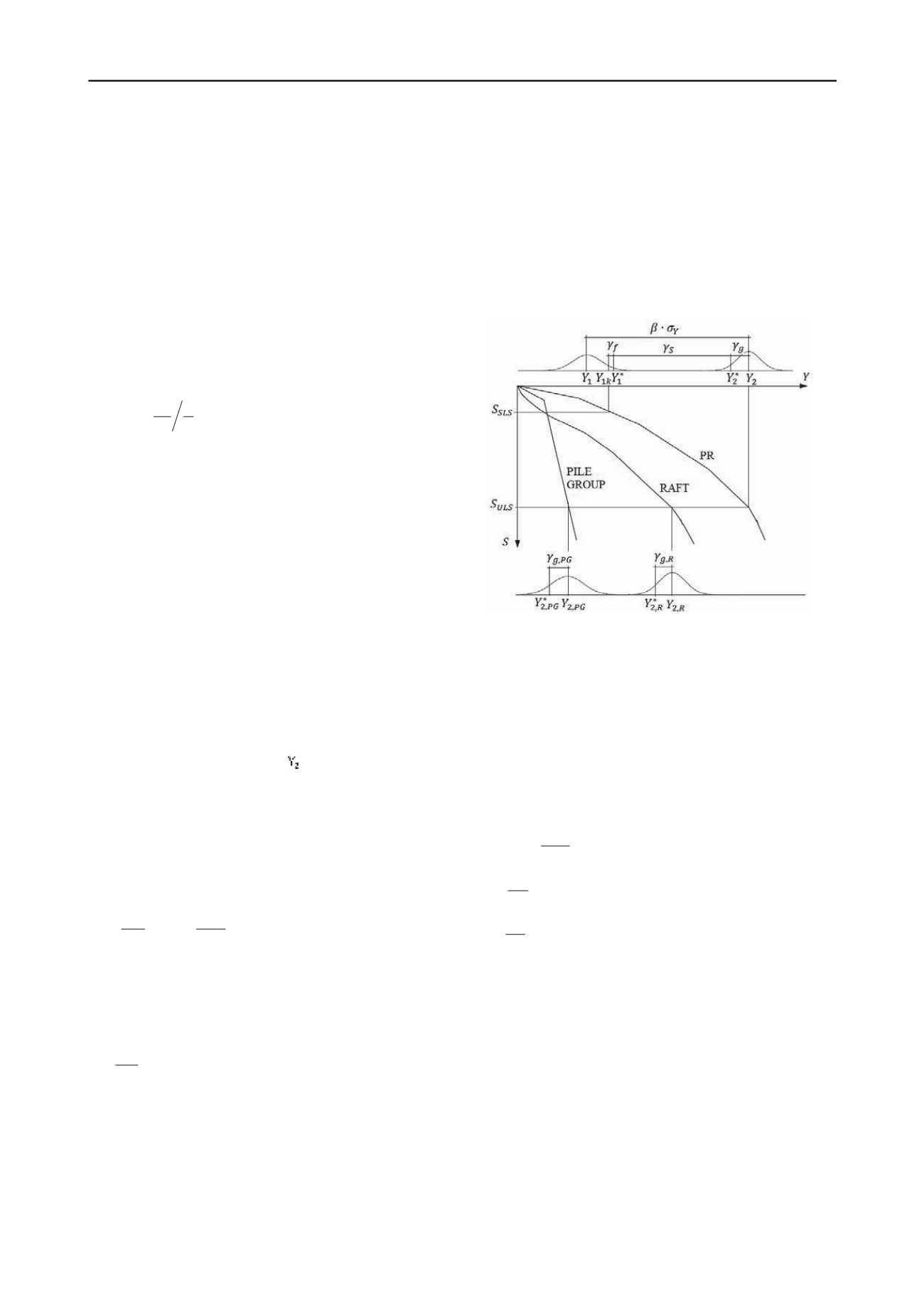
Figure 1 shows how LEM concepts are introduced in the PR
design. The resisting loads function is determined as the sum
of the raft average bearing capacity plus the respective one of
the pile group, as shown by the following equation:
2
2,
2,
PG
Y Y Y
R
(3)
where
2,
R
Y
and
2,
PG
Y
are the raft and piles bearing capacity,
respectively, calculated with average values of soil properties.
The design load function of each element of the system can be
obtained from the following equations:
2,
*
2,
,
R
R
g R
Y
Y
,
2,
*
2,
,
PG
PG
g PG
Y
Y
(4)
where
*
2,
R
Y
and
*
2,
PG
Y
are raft and the pile´s resistant loads,
respectively. They can be calculated from the design values of
the soil mechanical properties.
By mean of the former definitions and Figure 1 it is possible to
obtain the design equation for the ultimate limit state of a PR.
*
*
PR
S
Q P
(5)
where is the overall vertical design load;
*
P
S
is a partial
coefficient that considers the quality of the construction and the
type of failure;
*
PR
Q
is the design load capacity of the PR
obtained from equation 6.
*
*
where
and
*
UR
Q
*
PG
Q
are the raft and the piles design bearing
capacity respectively, calculated separately from the soil design
values.
The overall vertical design load can be obtained as a sum of the
individual characteristic load weighted by a particular
coefficient, as shown in the following equation:
*
ki
fi
P P
(7)
where is the characteristic loads and
P
ki
fi
are the weighting
coefficients for the loads.
Figure 1. Introduction of safety by the LEM in PR (Lorenzo 2010)
In this article, the resistant load function and its design values
are obtained in a manner that differs from the way they are
normally obtained in structural analyses. As suggested by
Quevedo (1987), Becker 1996), Gonzalez-Cueto (2000) and
Lima (2006), the soil properties coefficients are applied directly
to the mean values, while in structural design they are applied to
the characteristics values.
The design soil properties are calculated from values obtained
from the statistical processing of laboratory tests results,
weighting them by partial coefficients, as shown in equations 8,
9 and 10.
*
1
tan
tan
gtg
(8)
*
gC
C C
(9)
*
g
(10)
where
,
and
C
are the mean values of the soil internal
friction angle, cohesion and specific weigh, respectively; and
gtg
,
gC
,
g
are the partial safety coefficients that affect
each soil property.
4 APLICATION OF SAFETY THEORY TO THE
GEOTECHNICAL DESIGN OF PRF
By means of probabilistic methods it is possible to calibrate the
partial safety coefficients to be used in the LEM. This approach
has not yet been introduced in the design codes. Consequently,
the loads and resistance partial coefficients have not been
establish as well. Nevertheless, the necessary expressions for
the calibration of partial coefficients to use in the LEM can be
developed by means of the general procedure described in
Quevedo (1987). This author applied the procedure to the
design of shallow foundations in cohesive soils and
*
PR
UR UR
PG
Q
Q Q
(6)


