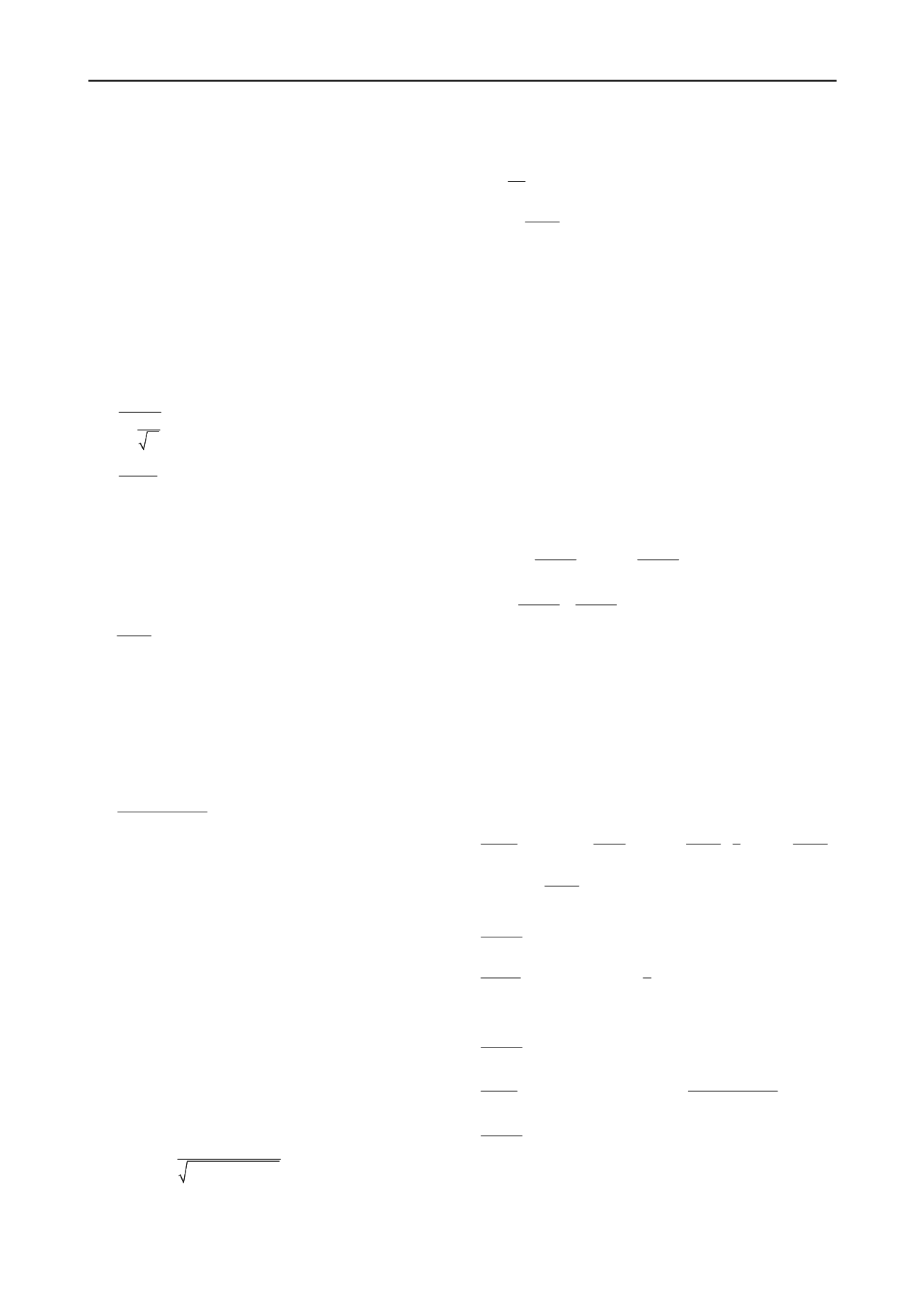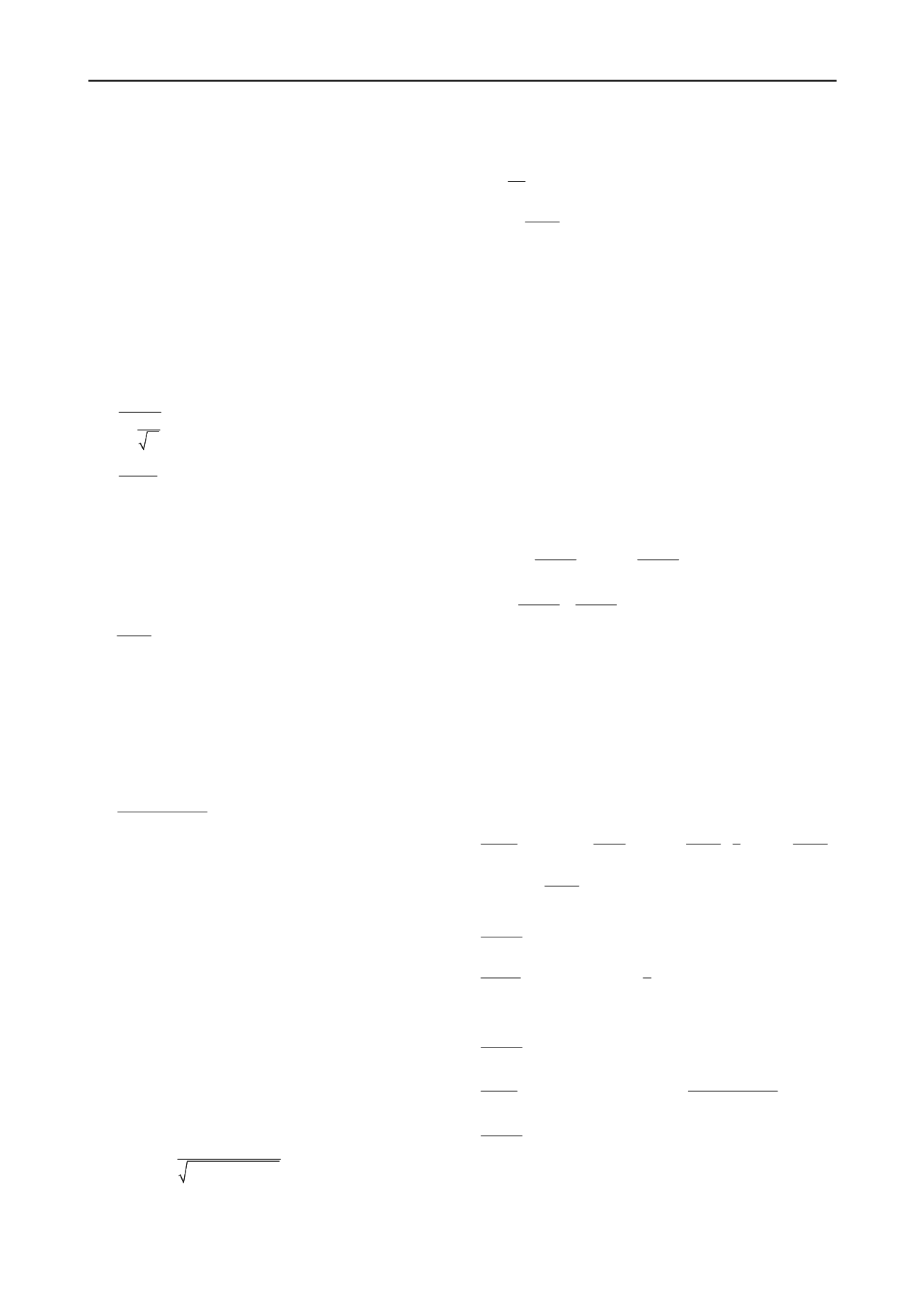
2801
Technical Committee 212 /
Comité technique 212
subsequently, Gonzalez-Cueto (2000) applied it to the design of
shallow foundations in frictional soils. Lima (2006) used the
approach in the design of drilled caisson’s foundation and
anchorages.
The procedure to calibrate the weighting coefficients by this
methodology requires the calculation of the global safety factor
(
,
s d
F
) and the optimal safety factor. The global safety factor is
associated with the partial coefficients introduced in the design
by the LEM. The optimal safety factor is determined with the
application of the probabilistic methods.
e soil can be
respectively calculated from equations 12 and 13.
1.1
Global Design Safety Factor
The weighting coefficient that are applied to adjust the soil
specific weight and the mechanical properties of th
1
1
gi
i
i
t v
n
(12)
1
1
i
v
Where
t
is the t-student function value for α = 0.95 at n-1
degrees of freedom;
v
i
is the coefficient of variation of the
i
soil
property;
n
i
is the amount o
gi
t
(13)
f repetitions of the test where the
i
resistant loads can be
obtained from th
soil property was obtained.
The partial safety coefficient of the
e following equation:
,
*
PR ult
g
PR
Q
Q
(14)
here
W
g
is the aforementioned coefficient.
In order to calculate
,
PR ult
Q
and
*
PR
Q
Equations 1 and 6 can be
sed, respectively.
coefficients of the loads can be calculated from
equation 15.
u
The weighting
1
ki
fi
f
ki
i
P t v
P
(15)
Finally, the global design safety factor can be obtained as:
,
s d
f
g s
F
(16)
1.2
Optimal Safety Factor
In order to obtain the optimal safety factor
,
s o
F
it is necessary
to deal with equations that are more complex than th se used to
obtain the global safety fac The load function (
1
Y
) and the
resistant ca
o
tor.
pacity function
2
Y
can be defin the following
equatio
ed by
ns:
1
Y P
(17)
2
,
PR ult
Y Q
(18)
leve
is related
to the
Where
P
is the mean value of the loads.
In the design of a PR, the required safety l
req
H
,
s o
F
by means of the equation 19.
2
2
2
,
P
S QPR u
F v
Where
n
As
P
v
and
,
PR ult
Q
v
are unknown, they can be expressed as:
P
P
v
P
(20)
,
,
,
PR ult
PR ult
Q
PR ult
v
Q
(21)
where
P
and
,
PR ult
Q
are the standard deviation of the total
vertical load and the ultimate bearing capacity of the PR,
respectively.
Taking into account that the total load is the result of the sum of
independent loads, which are values that represent random
variables, the standard deviation of the total vertical load can be
obtained as the sum of the standard deviation of each load, as
shown by the following equation:
2
2
P
Pi
(22)
where
Pi
is the standard deviation of the
i
vertical load.
The bearing capacity of the PR is a function that depends on
several random variables. This increases the complexity of the
calculation of the standard deviation. As shown in Lorenzo
(2010), it is possible to apply the Taylor`s series method where
the linearization of the function is combined with application of
the general theorem of standard deviation. With this, the
standard deviation can be expressed by:
,
2
2
,
,
2
2
tan
tan
PR ult
PR ult
PR ult
Q
Q
Q
C
,
,
tan
tan
2
tan
PR ult
PR ult
C C
Q Q
r
C
(23)
where
is a correlation coefficient between the cohesion
and the tangent of the friction angle.
r
C
tan
The derivatives on Equation 23 can be obtained from the
bearing capacity equations presented in (CTE 2006). This leads
to equations 24 to 29. In order to simplify the expressions, the
depth coefficients of the bearing capacity equations are
considered to be 1. This does not introduce a significant error,
because the contribution of the soil above the foundation is a
small percent of the total load. Equations 24 to 26 can be used
in a drained type analysis. These expressions become more
simple for cohesive soils in an undrained analysis, leading to
equations 27 to 29, as follows.
,
1
2
1
tan
tan
tan 2
tan
q
PR ult
c
UR
C
q
dN
dN
Q
dN
A C S
d S
B S
d
d
d
'
'
tan
q
P Vp
F V
dN
n A
A k f
d
(24)
,
PR ult
UR
C C
Q
A S N
c
(25)
,
1
2
PR ult
UR
q q
p q
F
Q
A d N S
B S N
n A N L A L k f
(26)
,
0
tan
PR ult
Q
(27)
,
2
100
200
5,14
100
PR ult
U U
UR
p E F
U
Q
C C
A n A F A
c
C
(28)
,
0
PR ult
Q
(29)
1
0.5
s
req
n
lt
F
H
(19)
is the error function,
P
v
and
,
PR ult
Q
v
the coefficient of
variation of
The standard deviation of the soils properties can be expressed
by equations 30 to 32.
tan
tan
.tan
(30)
.
c
c
C
(31)
the loads and the ultimate bearing capacity,
respectively.