848
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
where
4 4
4 4
f
(M ) / (M )
.
0
50
100
150
0
50
100
150
OCR=1
OCR=2
OCR=4
CSL
q
: kPa
0
50
100
150
200
0
50
100
150
200
OCR=2
OCR=4
OCR=8
CSL
5.2 Yield functions
The parameter of time effects is assumed to be
t
and
incorporated into the current yield function. So the current yield
function of the EVP UH model is assumed as
2
s
t
3
2
x0
p
1
ln
ln 1
+ 0
c
M
p
f
t
p
H H
(14)
Because the yield function is also workable in the isotropic
compression, the function of
t
can be obtained by substituting
η
=0 into eq. (14).
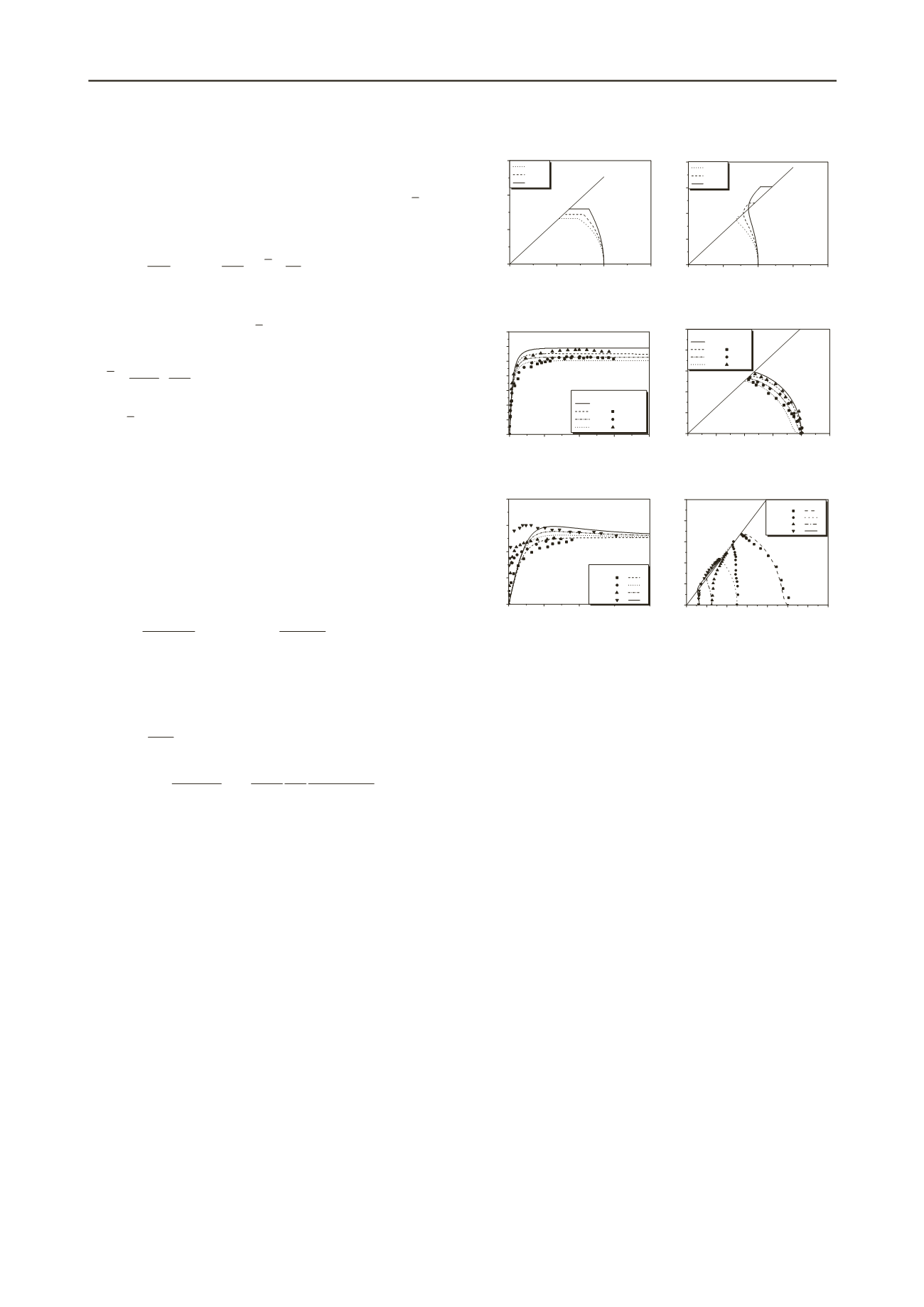
Figure 7. Stress paths of shear creeps: (a) at low stress ratios, and (b) at
high stress ratios.
0.00 0.05 0.10 0.15 0.20
0
50
100
150
200
250
300
350
Shear strain rate:%/h
Predicted� Measured�
Infinity
15
15
1.5
1.5
0.15
0.15
0 100 200 300 400 500
0
100
200
300
400
500
Shear starin rate:%/h
Predicted: Measured
Infinity
15
15
1.5
1.5
0.15
0.15
4
α
e
f
4
C M =
λ κ M
t
R
d
t
(15)
where
t
is not the real time but the equivalent time, indicating
the time effects on clays. In the proposed model, INCL
represents the instantaneously normally consolidated states and
its position is not affected by time. Therefore, the EVP model
still takes eq. (5) as the reference yield function. However,
when time effects are considered, the plastic volumetric strain
consists of both the strains due to stresses and time, i.e.,
p sp tp
v v v
.
Figure 8. Comparison between predicted and measured results of
triaxial undrained compressions at various rates.
0.00 0.05 0.10 0.15 0.20
0.0
0.5
1.0
1.5
2.0
Test Predicted
OCR=1
OCR=2
OCT=4
OCR=8
p
/
p
c
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4
0.0
0.2
0.4
0.6
0.8
1.0
Test Predicted
OCR=1
OCR=2
OCR=4
OCR=8
5.3 Constitutive relationship
The time has no effects on the elastic law. So the elastic strain
increments are still calculated by Hooke law.
e
v
3 1 2
d
d
p
E
e
d
2 1
d
d
3
q
E
(16)
where
is the Poisson’s ratio. The elastic modulus is
. The plastic strain rate can be
expressed as:
1 2
E
0
3(
)(1 ) /
e
Figure 9. Comparison between predicted and measured results of
triaxial undrained compressions on clays having different
initial OCRs.
p
7 CONCLUSIONS
p
ij
ij
f
s
t
4 2 2 2
e f
p
2 2
4 4 4
0
f
C
2
M (M )
c
1
M
M M
p
q
e
pR
(17)
s
and
are the time-independent and time-dependent
plastic factor, respectively. and are the rates of stresses.
t
p
q
This paper established a new EVP framework by assuming the
existence of the instant normal compression line. Furthermore,
the 1-D EVP relationship was proposed by adopting the
reloading line of the UH model as the instant compression line.
Then with the equivalent time incorporated into the current
yield function of the UH model, the 3-D EVP model was built.
Compared with MCC, the proposed model needs only one
additional parameter (the coefficient of secondary compression).
5.4 Shear creep
Figure 7 shows calculated stress paths of the undrained creeps
with constant shear stresses. In the predictions, clays are
instantaneously loaded first. Then the shear stresses remain
unchanged in order to make clays creep under time effects. The
paths in Figure 7(a) and Figure 7(b) are for low stress ratios
(
q
/
p
<M
Erreur ! Source du renvoi introuvable.
) and high
stress ratios (
q
/
p
>M), respectively. The values of parameters
adopted are shown in the row “3-D” of Table 1.
8 REFERENCES
Bjerrum L. 1967. Engineering geology of Norwegian normally-
consolidated marine clays as related to settlements of buildings.
Geotechnique
17(2), 83-118
Kutter B.L. and Sathialingam N. 1992. Elastic viscoplastic modelling of
the rate-dependent behaviour of clays.
Geotechnique
42(3), 427-
441
Yao Y.P., Gao Z.W., Zhao J.D., et al. 2012. Modified UH model:
constitutive modeling of overconsolidated clays based on a
parabolic Hvorslev envelope.
J Geotech Geoenviron Eng
138(7),
860-868
6 VERIFICATION
The predicted results by the proposed model are compared with
the test data of Hong Kong Marine Deposits (Zhu 2000). The
parameters are displayed in the row “3-D” of Table 1.
Yao Y.P., Hou W. and Zhou A.N. 2009. UH model: three-dimensional
unified hardening model for overconsolidated clays.
Geotechnique
59(5), 451-469
Figure 8 shows the predicted and measured results of the
triaxial undrained compressions at various constant strain rates
on clays having the same initial OCR
.
Figure 9 illustrates the
predicted and measured results of tests at the same constant
strain rate (1.5 %/h) on clays having different initial OCRs.
Because the confining pressures imposed on clays of various
OCRs are different from each other, the results are normalized.
Yin J.H., Zhu J.G. and Graham J. 2002. A new elastic viscoplastic
model for time-dependent behaviour of normally and
overconsolidated clays: theory and verification.
Can Geotech J
39(1), 157-173
Yin Z.Y., Chang C.S., Karstunen M., et al. 2010. An anisotropic elas-
tic-viscoplastic model for soft clays.
Int J Solids Struct
47(5), 665-
677
Zhu J.G. 2000.
Experimental study and elastic visco-plastic modelling
of the time-dependent stress-strain behaviour of Hong Kong marine
deposits
. Hong Kong: The Hong Kong Polytechnic University


