844
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
property of soil and have been described using viscoplastic
constitutive equations. In contrast, the results presented here
demonstrate that delayed failure and the existence of a threshold
load value for the occurrence (or lack thereof) of delayed failure
can be simulated as a soil-water coupling effect without having
to impose a time dependence on the soil skeleton. The time
history of vertical acceleration of the central node of the
foundation around the time of delayed failure for the 128 kPa
load case is presented in Figure 10. Similar to the behavior
observed in the load-controlled case in Figure 6, it is evident
that the behavior during failure involves accelerated motion. As
such, it is necessary to account for inertial force in order to
reproduce the behavior that occurs during this delayed failure.
Furthermore, in the 128 kPa load case presented in Figure 8, the
momentary increase in displacement velocity followed by a
secondary convergence indicates a return to static consolidation
following the convergence of accelerated motion. Thus, the soil-
water coupling effect is particularly important in understanding
the consolidation behavior before and after failure, and the
effects of inertial force are particularly important in
understanding the dynamic failure experienced under constant
load. It should be kept in mind that even if it is possible to
reproduce the behavior of the ground right up to the point of
failure by using a time-dependent constitutive equation, if the
analytical tool used to solve the boundary value problem does
not account for inertial force, it will not be possible to reproduce
the behavior after that point.
100
(%)
s
0
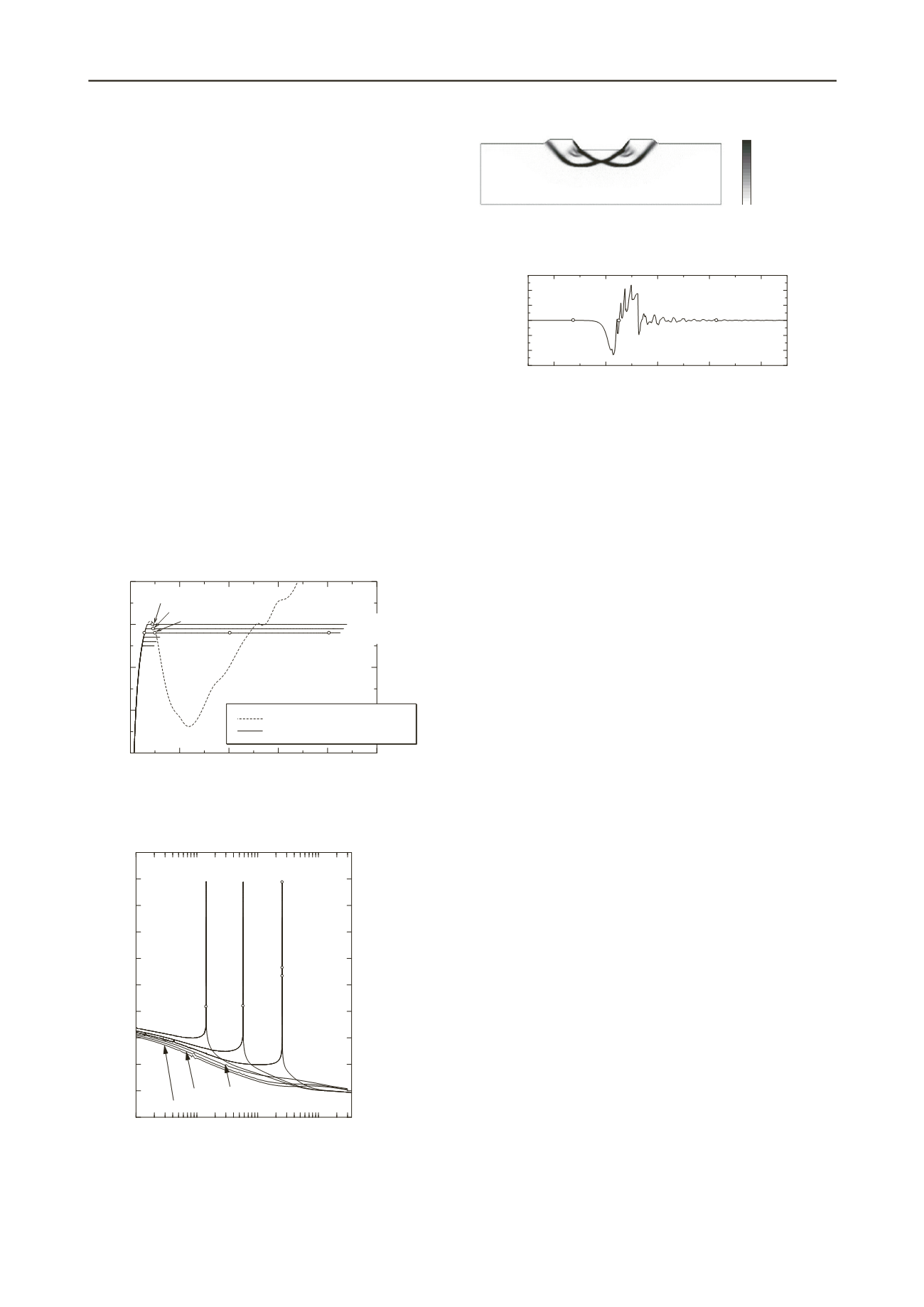
(c) After delayed failure
Figure 9. Distribution of shear strain (load: 128 kPa)
227506 227508 227510 227512 227514
-300
-200
-100
0
100
200
300
Acceleration (cm/sec
2
)
(b)
(a)
(c)
Time (sec)
Figure 10. Time history of acceleration of central node of foundation
(load: 128 kPa)
5 CONCLUSIONS
In this paper, a bearing capacity analysis was carried out for a
highly structured naturally deposited clay ground using the soil-
water coupled finite deformation analysis code
GEOASIA
,
which takes inertial forces into consideration and employs the
SYS Cam-clay model, which is capable of describing the work
of the soil skeleton structure. The following results and
conclusions were obtained.
0
20
40
60
80
100
100
110
120
130
140
Settlement (cm)
Vertical load (kPa)
129 kPa
130 kPa
128 kPa
127 kPa
126 kPa
(o)
(a)
(b)
(c)
displacement controlled case
load controlled case
(a)'
(a)"
125 kPa
1) When a ground that exhibited localization of deformation
and formation of a circular slip failure accompanied by load
reduction as a result of loading by displacement control was
loaded by load control, it failed dynamically in association
with acceleration motions after reaching the peak load
obtained during displacement control.
2) To date, the bearing capacity problem has only been dealt
with quasi-statically, but it is essential to take inertial forces
into consideration in order to reproduce this type of failure
behavior.
Figure 7. Relationship between vertical load and settlement (load
constant case)
3) Using the analysis code, it was possible to reproduce the
behavior before, during, and after the delayed failure
phenomenon, as well as whether or not there is a load
threshold for occurrence of delayed failure. To reproduce
this type of phenomenon, a time-dependent constitutive
equation is not necessarily required as an inherent nature of
soil skeleton.
10
-2
10
-1
10
0
10
1
10
-2
10
-1
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
10
8
Time (day)
Displacement velocity (cm/day)
q
= 128 kPa
q
= 129 kPa
q
= 127 kPa
q
= 126 kPa
q
= 130 kPa
q
= 125 kPa
(a)
(c)
(b)
(a)'
(a)"
4) For the delayed failure phenomenon, the soil-water coupling
effect is particularly important for the consolidation
behavior before and after failure, and inertial effects are
particularly important for the dynamic failure behavior
while a constant load is maintained.
6 REFERENCES
Asaoka, A., Nakano, M. and Noda, T. 1994. Soil-water coupled
behaviour of saturated clay near/at critical state,
Soils and
Foundations
, 34(1), 91-106.
Asaoka, A., Noda, T., Yamada, E., Kaneda, K. and Nakano, M. 2002.
An elasto-plastic description of two distinct volume change
mechanisms of soils,
Soils and Foundations
, 42(5), 47-57.
Noda, T., Asaoka, A. and Nakano, M. 2008. “Soil-water coupled finite
deformation analysis based on a rate-type equation of motion
incorporating the SYS Cam-slay model.”
Soils and Foundations
,
45(6), 771-790.
Asaoka, A., Noda, T. and Kaneda, K. 1998. Displacement/traction
boundary conditions represented by constraint conditions on
velocity field of soil,
Soils and Foundations
, 38(4), 173-181.
Noda, T., Asaoka, A. and Yamada, S. 2007. Some bearing capacity
characteristics of a structured naturally deposited clay soil,
Soils
and Foundations
, 47(2), pp. 285-301.
Figure 8. Relationship between time and displacement velocity (load
constant case)
Murayama, S. and Shibata, T. 1956. On the Rheological characters of
clay,
Journal of JSCE
, 40, 1-31, in Japanese.


