846
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
hardening parameter of MCC into the unified hardening
parameter
H
that is expressed as
4 4
p
f
v
4 4
M d
M
H H
d
(3)
where
p
v
is the total plastic volumetric strain.
By combining the elliptical yield function and the unified
hardening parameter, the current yield function of the UH
model can be written as
2
1
2
x0
p
1
ln
ln 1
0
c M
p
f
p
H
(4)
where
p
x0
is the initial intersection point of the current yield
surface and axial
p
. c
p
=(λ−κ)/(1+
e
0
). λ is the slope of the normal
compression line (NCL) in
e
-ln
p
plane, κ the slope of rebound
curve in
e
-ln
p
plane,
e
the void ratio and
e
0
the initial void ratio.
Because the reference surface represents the normally
compressed states of clays, the UH model adopts the yield
function of MCC as the reference yield function.
2
p
2
v
2
x0
p
1
ln
ln(1 )
0
c M
p
f
p
(5)
where
x0
p
is the initial intersection point of the reference yield
surface and axial
p
.
3 INSTANT NORMAL COMPRESSION LINE
3.1 Instant compression and delayed compression
As shown in Figure 2, in tests the isotropic compression
represented by NCL experiences some test time because of the
limitation of permeability. If clays creep for the same time from
different points on NCL, such as C and C′, the final states will
shape a line parallel to NCL, i.e., CD=C′D′ (Bjerrum 1967).
With the creep time changing, the line of final states will move
and form a series of parallel lines, as shown as lines “1 Day”,
“10 Days” and “100 Days”. In light of this phenomenon, it is
inferred that above NCL there must be a compression line for
which the creep time is “0”. The line reflects the normally and
instantaneously compressed characteristics of clays. Thus, it is
called instant normal compression line (INCL) in this paper.
If remolded clays prepared in tests are assumed to be not
influenced by time, their states can be represented by point A on
INCL in Figure 2. ACD is the consolidation process which is
traditionally divided into primary compression AC and
secondary compression CD. However, the time of the primary
compression of soft clays is so long that creep also exists in the
primary compression. So the consolidation was divided into
instant compression and delayed compression in accordance
with the concept of INCL. That is to say, ACD is equivalent to
ABD that includes instant compression AB and delayed
compression BD. In the instant compression, the total stresses
are supposed to be imposed on the clay skeleton
instantaneously. In the delayed compression effective stresses
are constant, and the clay deforms only due to the time.
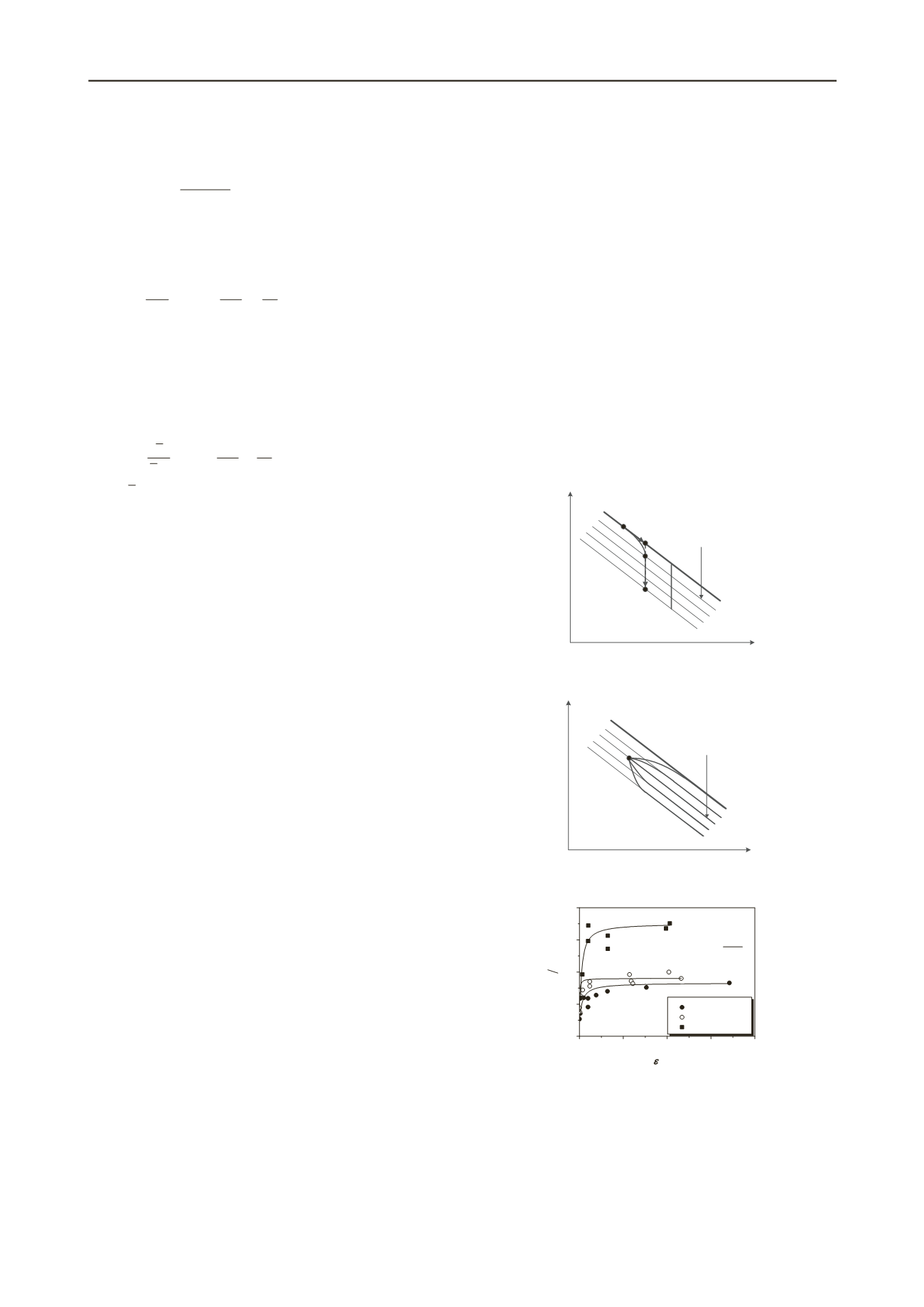
3.2 One-dimensional (1-D) rate effect
As shown as in Figure 3, the curves of isotropic compressions at
various constant strain rates are all parallel to INCL. Moreover,
when the volumetric strain rate is larger, the position of the
loading curve is higher, i.e., the apparent preconsolidation
pressure
p
ac
is increasing with the strain rate. Figure 4 illustrates
the results of 1-D oedometer consolidation tests with constant
strain rates on several kinds of clays (Yin et al. 2010).
v
is the
volumetric strain rate and
p
0
the initial mean effective stress.
The results are fitted by the hyperbolic function. The positive
correlation between
p
ac
and the volumetric strain rate is obvious.
However, the change of
p
ac
is decreasing gradually with the
strain rate increasing. When the strain rate is large enough, the
change of
p
ac
is small. Therefore, this paper assumed that the
value of
p
ac
will not vary when the rate is large enough. That is,
while the rate keeps increasing, the loading curve in Figure 3 is
not going to move upwards indefinitely, and there will be a
bounding line which is actually INCL.
4 1-D EVP RELATIONSHIP
According to the concept of INCL and the theory of instant
compression and delayed compression, the total volumetric
strain is additively decomposed into the following:
s
t
se sp tp e p
v v v v v
v
v v
(6)
where
s
v
is the volumetric strain under effective stresses, i.e.
the instant strain including elastic strain
se
v
and plastic strain
sp
v
.
t
v
denotes the volumetric strain influenced by time
effects, i.e., the delayed strain. The strain due to time effects is
irreversible, so
t
t
v v
p
.
e
v
is the elastic volumetric strain that
only occurs on account of stresses.
p
v
is the plastic volumetric
strain containning
sp
v
and
tp
v
.
Figure 2. Division of isotropical consolidation process.
1
v
2
v
3
v
4
v
1
2
3
4
v
v
v
v
Figure 3. Schematic graph of 1-D rate effect.
1
s
v
ac 0
p p
b
y c
x a
0.0 5.0x10
-6
1.0x10
-5
1.5x10
-5
2.0x10
-5
0.5
1.0
1.5
2.0
2.5
Backebol clay
Berthierville clay
Bothkennar clay
Figure 4. Relationships between apparent preconsolidation pressure and
volumetric strain rate (Yin et al. 2010).
4.1 Instant strain
The proposed model adopts the function of the reloading line of
the UH model to calculate the instant strain. Assuming
η
in eq.
(4) to be zero and considering the elastic strain, the 1-D stress-
strain equation of the UH model can be expressed as


