2772
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Although a full three dimensional (3D) analysis is preferable
when studying problems involving piles, in the present study a
two dimensional (2D) approach under axisymmetric conditions
was used in order to reduce the computation time. This means
that, even though the real raft shape was rectangular, a circular
raft was simulated. The raft had a radius of 2.257 m, giving it
the same area as the real raft. The pile had a radius of 600 mm
and was straight, with no base enlargement. From the top
surface, the simulated soil layers were clay 1 (4 m), sand 1 (4
m), sand 2 (13.5 m), clay 2 (6.5 m) and clay 3 (12 m), as shown
in figure 2. The material parameters were determined by
consolidation testing of clay 1 and drained triaxial compression
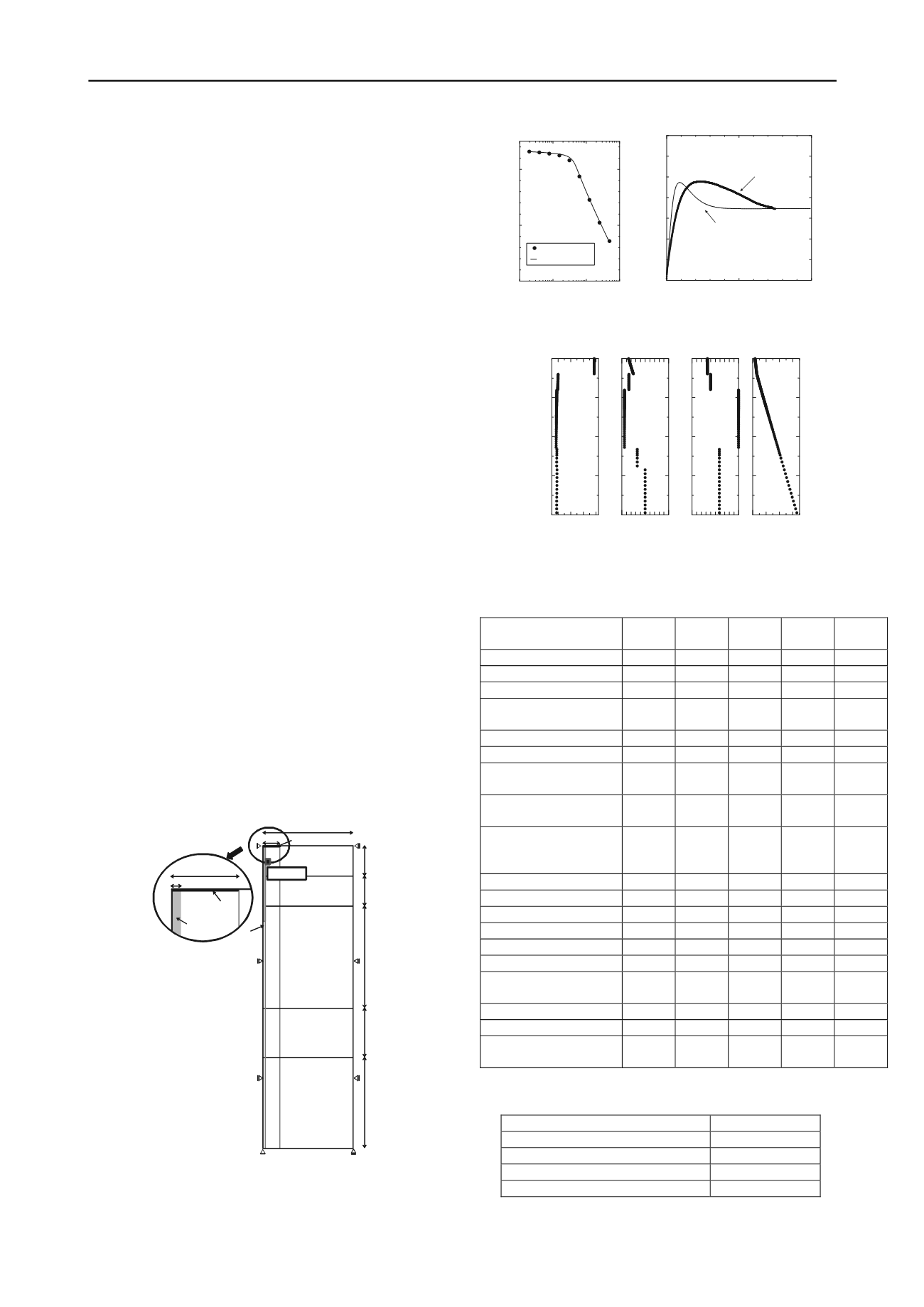
testing of sand 2. Figures 3a (clay) and 3b (sand) compare the
simulated and laboratory test results. For clay, the simulated and
experimental results agree well, but for sand, the initial
simulated modulus differs from the experimental data. This is
because the parameters of the simulated sand were chosen to
allow later simulation of a loading experiment. Table 1 shows
the soil material parameters. Due to the lack of experimental
data, some of the material parameters for clays 2 and 3 were set
to be the same as those for clay 1, but with different initial void
ratios. Similarly, some of the material parameters for sand 2
were set to be the same as those for sand 1. Table 2 shows the
pile material properties, which correspond to the typical linear
elastic parameters of pre-stressed high-strength concrete. Figure
4 shows the initial simulated soil profile. A load of 19.2 kPa
was applied to the soil surface at the raft position to simulate the
load of the raft. Displacement of raft elements in the x direction
was restrained, but displacement in the y direction was allowed.
The stratified soil model was first prepared, after which
elements with properties corresponding to the pile material were
added. This was done while taking into account the force
equilibrium between the soil and pile elements. After the excess
pore pressure dissipated, a vertical displacement was applied to
the pile elements for the three different cases: Case 1 models the
raft alone, Case 2 models the pile alone, and Case 3 models the
piled raft foundation. Figure 5 shows the step loading process
followed during the actual physical experiment. The bearing
capacity is dependent on the loading speed as well as the load
magnitude. In the simulation, even though cyclic loading was
not taken into consideration, the loading rate was set to a fixed
value of 0.01 mm/sec in consideration of the final 10 cm
settlement (Kaneda
et al.
(2012)).
4m
4m
13.5m
6.5m
12m
clay1
sand1
sand2
clay2
clay3
11.9m
2.257m
0.3m
2.257m
pile
pile
raft
raft
Aelement
Figure 2: Boundary conditions
10
1
10
2
10
3
10
4
1
2
3
Vertical Pressure (kPa)
Void Ratio
Experimantal data
Simulation
10
20
0
200
400
600
Axial strain (
%
)
Deviator stress (kPa)
Experimental data
Simulation
(a) Clay 1 (b) Sand 2
Figure 3: Experimental and simulation results
1 2 3 4
0
20
40
0 0.5 1 0 0.5 1
0 100200300
Void ratio
e
R
(=1/O.C.R.) State of structure
Height (m)
Vertical Stress
R
*
σ
v
(kPa)
Figure 4: Initial soil conditions
Table 1: Material properties of soils
<Elasto-plastic
parameter>
Clay 1
Sand 1
Sand 2
Clay 2
Clay 3
Compression index λ
0.50
0.050
0.050
0.10
0.10
Swelling index κ
0.02
0.012
0.012
0.015
0.015
Critical state constant M
1.45
1.36
1.36
1.26
1.26
NCL intercept N
(at
p
’ = 98 kPa)
4.3
1.98
1.98
2.00
2.00
Poisson’s ratio ν
0.1
0.1
0.1
0.3
0.3
<Evolution parameters>
Degradation parameter
of structure
a
0.8
2.2
2.2
0.8
0.8
Degradation parameter
of structures
b
and
c
1.0
2.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
Degradation parameter
of overconsolidated state
m
5.0
1.0
1.0
1.2
1.2
Evolution parameter
b
r
0.001
1.00
1.00
0.150
0.150
Limit of rotation
m
b
1.0
0.6
0.6
1.0
1.0
Permeability
k
(cm/sec)
1.0
-7
4.0
-3
4.0
-3
1.0
-7
1.0
-7
Density ρ
s
(g/cm
3
)
2.631
2.631
2.631
2.65
2.65
<Initial conditions>
Void ratio
e
3.87
Overconsolidation ratio
1/
R
0
6.5
17.0
3.0
2.0
Degree of structure 1/
R
*
0
3.0
2.5
1.0
1.7
1.7
Degree of anisotropy ζ
0
0.545
0.545
0.75
0.545
0.545
Coefficient of lateral
pressure
K
0
0.6
0.6
0.5
0.6
0.6
Table 2: Pile material properties
Pile
Elastic modulus E (kPa)
47360000
Poisson’s ratio ν
0.2
Density ρ (g/cm
3
)
2.3
Coefficient of lateral pressure
K
0
0.0


