2761
Technical Committee 212 /
Comité technique 212
2.3
Prediction model for skin friction of floating-type column
In this study, in order to evaluate the skin friction applied
around the surface of floating-type columns, FEM analysis with
the Cam-clay model as the constitutive equation was performed
using axi-symmetric and plane strain models (Ishikura et al.,
2006).
H
,
H
1
and
L
denote the ground depth, the improvement
depth and the distance between the improved columns or walls,
respectively. The ground surface was deformed equally by the
rigid plate on the assumption of shallow stabilized ground.
From the results of FEM analysis, the upward skin friction
applied around the surface of the improved column is
determined using the approximate formula given in Eq. (1).
LH p
c
p
u
/
1
1 0 0
·
(
�
)
(1)
u
c
p
0
denotes the pre-consolidation pressure of the soft clay.
denotes the averaged skin friction applied around the surface of
the column. This value is obtained from the difference between
the stress applied on and immediately below the improved
column. Each value of
is normalized by the
p
0
.
H
1
is
normalized by the value of
L
. The normalized average friction
0/
p
decreases with an increase in
H
1
/
L
. Furthermore, the
maximum value of
0 /
p
is almost equal to the shear strength
ratio
0
. It is clarified that
/
p uc
changes under several
conditions with different values of
H
,
H
1
, and
L
.
Here,
u
is the undrained shear strength. The approximate
curve almost corresponds to the relationship between the
upward averaged skin friction and the improvement parameters.
c
It is considered that skin friction is mobilized around surface
acting relative displacement between the column and soft clay.
The combined foundation transfers the load to the pile group via
the raft; hence soft clay between the friction piles in the upper
part of the combined foundation is enclosed.
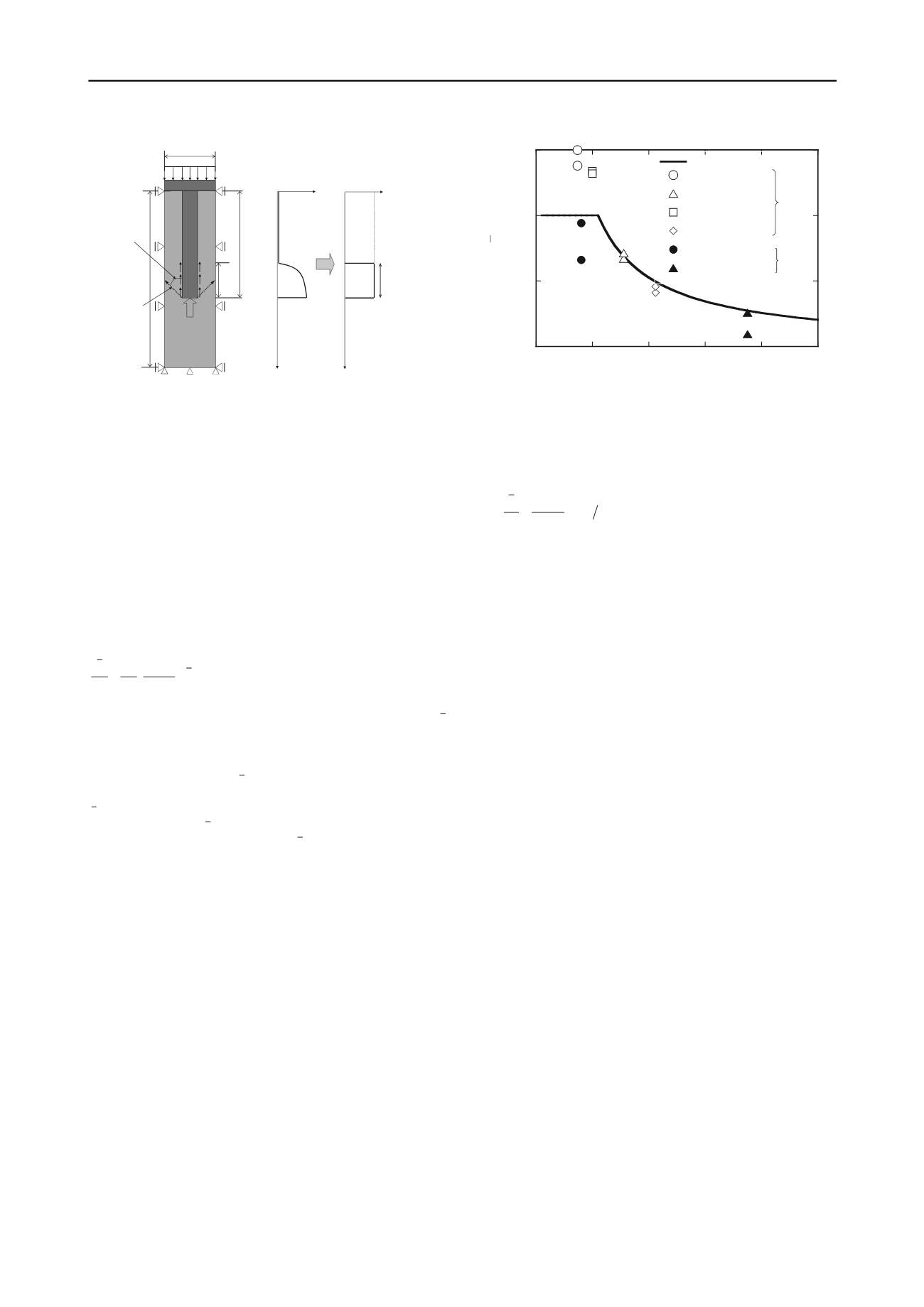
Figure 6 shows the hypothesis of skin friction around the
surface of columns. As shown in this figure, if the slip surface
that has inclination of 45 degrees from the pile end to the upper
part has occurred, the intersection adjacent the column has been
existed. When the length from this intersection to the column
end is supposed the length that the skin friction is mobilized, the
equivalent conversion ratio
which is defined as the ratio
between the column length and the length that the skin friction
is mobilized is introduced in Eq.(2).
(2)
1
/
HL
When
u
is defined as the undrained shear strength near the
surface acting relative displacement between the column and
soft clay,
c
is also given in Eq.(3) by using Eq.(1).
0
0.5
1
1.5
0
1
2
3
4
5
Approximated formula
H
1
/
H
= 0.55, 1pile
H
1
/
H
= 0.55, 5piles
H
1
/
H
= 0.75, 1pile
H
1
/
H
= 0.75, 5piles
H
d1
/
H
= 0.74, 1pile
H
1
/
H
= 0.74, 3piles
α
=
τ
/
c
u
H
1
/
L
Group
column
Wall
45
°
+Φ/2
Slip
surface
L
H
1
αH
1
Skin friction
τ
Skin friction
τ
H
1
Modeling
c
u
αH
1
H
Depth
Depth
Figure6. Hypothesis of skin friction around the surface
Figure7. Formulation of equivalent conversion ratio
α
LH c
u
/
1
1
(
LH
1
�
1)
(3)
Figure7 shows the formulation of the equivalent conversion
ratio
. Experimental values of two types of loading model
tests were also plotted (group column type and wall type). As
shown in this figure, equivalent conversion ratio
nearly
corresponds with the calculated value from Eq.(2) or Eq. (3).
3
TENDENCY OF SKIN FRICTION MOBILIZATION IN
THE CONSOLIDATION PROCESS
3.1
Numerical modeling
In this section, in order to evaluate skin friction mobilization of
this type of improved ground during consolidation, time
dependent behaviors of skin friction were investigated by using
FEM analysis. Numerical analysis has already been performed
to investigate the neutral plane of pile in the consolidating
ground (Yan, W. M. et al., 2012). Figure 8 shows the Axi-
symmetric model for evaluating skin friction in this study.
Elastic model was applied to the shallow stabilized ground
(raft) and column (pile). Modified Cam-clay model was also
used in the soft clay as the constitutive equation. In this figure,
h
means the thickness of shallow stabilized ground,
H
1
and
L
means the column length and distance between columns.
H
and
d
also means the thickness of soft soil layer and column
diameter. In this analysis, in reference to the field measurement
(Ishikura et al., 2009),
h
,
H
1
,
d
,
L
was set to 1.0m, 6.5m, 1.0m,
2.0 m , respectively. Table1 shows the material parameters. The
ground water level was located at the ground surface of model
ground and drainage boundaries were set to the upper and lower
part of model ground. After applying to the 1 kPa on the ground
surface, 150 kPa of
Δp
was applied to the ground surface in the
assumption of fill with 7.5m. In this study, full shear resistance
of soil-pile interface was modeled by Eq.(4).
'
'
tan
n
f
R Rc
(4)
Here,
c
’
and means the effective cohesion and friction angle
of soil,
n
means the normal effective stress applied to the
interface and
R
means the interface friction coefficient. These
R
values were used in 0.90, 0.75, 0.50, 0.30, respectively.
'


