2264
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
6.4
Variable Intensity, Frequency and Waveform
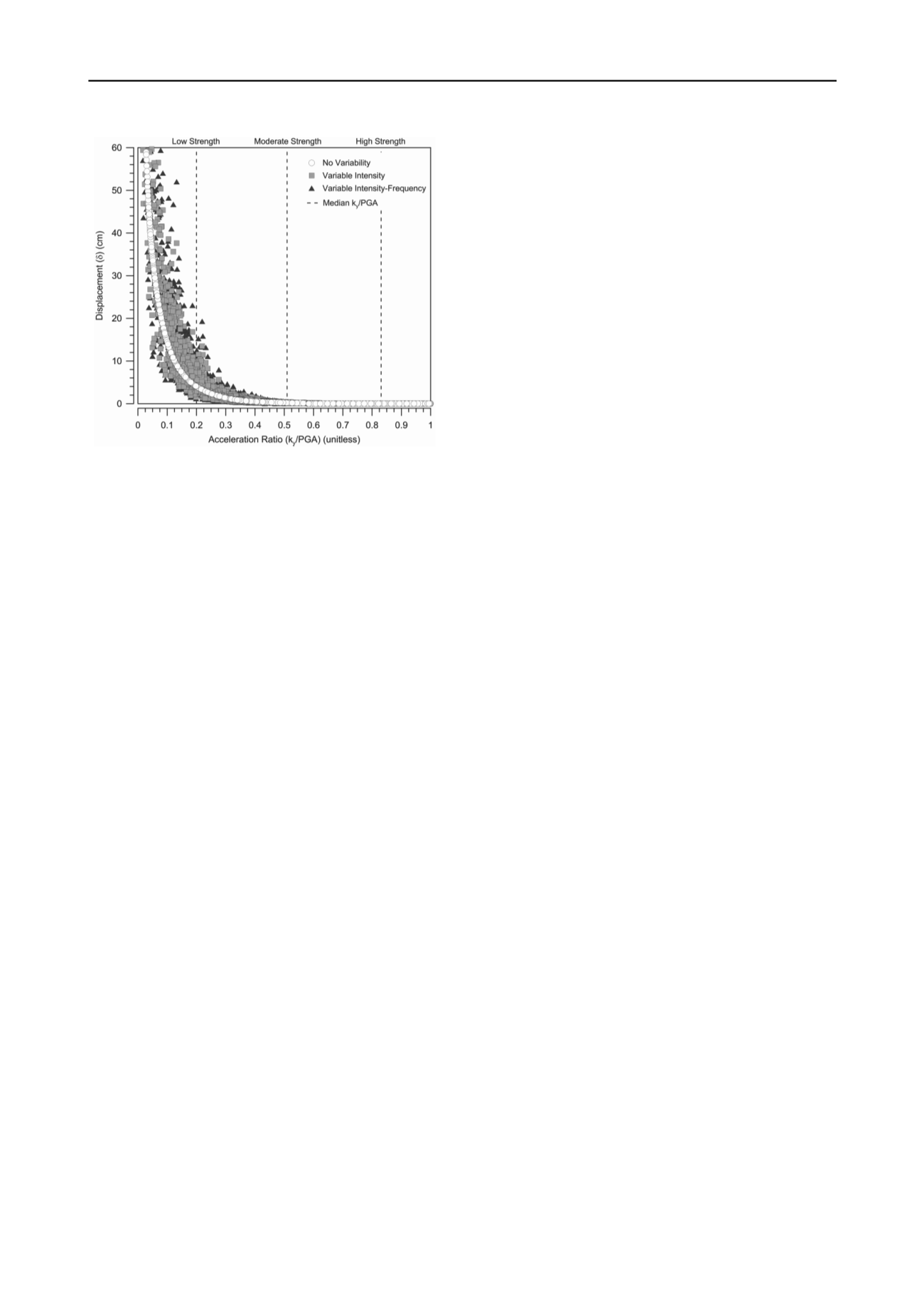
Figure 5. Comparison of the
-
k
y
/PGA
relationships for the LHA parent
motion for the different ground motion variability scenarios
From this it may be inferred that the displacement
uncertainty for marginally stable slopes is more sensitive to
variability in the site conditions (i.e., input parameters that feed
into
k
y
) while slopes with greater relative stability are more
sensitive to ground motion variability. This suggests that for
weaker slopes, greater resources and effort should be focused on
constraining the variability of the subsurface conditions,
whereas for more stable slopes the focus should be on
characterizing the earthquake ground motions.
When the intensity, frequency and waveform are varied, the
combined affect yields displacement uncertainty that is
marginally different from the previous case. Similar to
frequency, introducing more diverse waveforms has little effect
on the prediction uncertainty. However, it is interesting to note
that
IQR
for this scenario is sometimes greater or less than the
IQR
for the individual parent motions. This is related to the
wavelet-based spectral-matching process where the parent
motion is decomposed, scaled up/down using wavelets and re-
assembled such that modified time-history is compatible with
the spectrum and non-stationary characteristics of the parent
motion are preserved. Thus, even though the response spectra
varies between
3
bounds using only one parent motion
yields a suite of spectra-compatible motions that have very
similar non-stationary characteristics. This explains the
systematic differences between the four parent motions for three
previous ground motion variability scenarios. For example, the
non-stationary characteristics of the VAS and WPI motions are
such that when input into the “double-integration” computation
of the rigid-block method, regardless of being scaled or
spectrally matched, systematically yield higher median
displacements and more prediction uncertainty than motions
LHA and ORR. When all four motions are propagated through
the displacement analysis, the effects of individual motions are
tempered and a more average displacement response is
computed. This average response, however, is not necessarily
more precise than using a single parent motion.
7 CONCLUSIONS
6.3
Varied Intensity and Frequency
When additional variability from frequency content is
introduced into the analysis, marginal increases in the
displacement uncertainty are observed. This is indicated by the
slight increase in scatter in the
-
k
y
/PGA
data shown in Figure
5. For the four parent motions, displacement uncertainty
increases by a factor of about 1.2, this is substantially less
change than that observed when variability in intensity was
introduced into the analysis. This is consistent with research
that has demonstrated the efficiency of intensity ground motion
parameters (e.g.,
PGA
, peak ground velocity,
PGV
and Arias
Intensity,
I
a
) over frequency content parameters for correlating
with displacement predictions (Saygili and Rathje 2008).
While the range of response spectra simulated in the
analysis (Figure 2) do show variations in their spectra shape, the
peak spectral acceleration between the
3
bounds remains
constant at a predominant period (
T
p
) of about 0.2 s. This
characteristic as well as the frequency-smoothing affect that
spectral-matching has on the output motions could explain the
marginal increase in displacement uncertainty. It is likely that
displacement uncertainty would increase had the
T
p
of the
simulated response spectra been allowed to take on a range of
values. If, for example, the sub-model for site-conditions
(specifically
v
s30
) in the Abrahamson and Silva (2008) GMPE
had been modeled as a random variable this would have
generated more diverse spectral shapes and hence additional
variability in the ground motions. If this technique is
implemented in a probabilistic analysis it should be compatible
with the underlying assumptions of the method being used. For
example, the Newmark (1965) rigid-block model assumes that
the slope and slide mass are a non-deformable, rigid body. As
such it would be inappropriate to use motions spectrally-
matched to a response spectrum for site conditions
representative of soft soil as this implies that the slope and slide
mass can respond dynamically to the motions. In this case,
decoupled-type analyses such as Makdisi and Seed (1978)
would be appropriate.
Systematically increasing ground motion variability (and
complexity) in the probabilistic displacement analysis showed a
trend of increased displacement uncertainty. For the idealized
slope, this trend was consistent across a range of relative
stabilities (low, moderate and high). Ground motion variability
had its most pronouced affect on displacement uncertainty at
low acceleration ratios as a consequence of the non-linear
-
k
y
/PGA
relationship. Of the four scenarios considered,
variability in ground motion intensity alone has the greatest
impact on the displacement prediction uncertainty. When
additional variation in frequency content and waveform is
introduced, only minimal changes in uncertainty are observed.
These results suggest that displacement uncertainty may be
adequately characterized through simple scaling of ground
motion intensity and that the effort required to create variability
in both intensity and frequency through spectral-matching may
be of limited utility. Also, the use of mutliple parent motions in
a displacement analysis can overcome potential biases
introduced by individual motions, but may not always lead to
more constrained prediction uncertainty.
8 REFERENCES
Abrahamson N.A. and Silva W.J. 2008. Summary of the Abrahamson &
Silva NGA ground motion relations.
Earthquake Spectra
24, 67-97.
Makdisi F. I. and Seed H. B. 1978. Simplified procedure for estimating
dam and embankment earthquake-induced deformations.
Journal of
Geotechnical Engineering Division
104(GT7), 849-867.
Mukherjee S. and Gupta V.K. 2002. Wavelet-based generation of
spectrum-compatible time-histories.
Soil Dynamics and Earthquake
Engineering
22(9-12), 799-804.
Newmark N.M. 1965. Effects of earthquakes on dams and
embankments.
Géotechnique
15(2), 139-160.
Strenk P.M. and Wartman J. 2011. Uncertainty in seismic slope
deformation model predictions.
Engineering Geology
122(1-2), 61-
72.
Saygili G. and Rathje E.M. 2008. Empirical predictive models for
earthquake-induced sliding displacements of slopes.
Journal of
Geotechnical and Geoenvironmental Engineering
134(6), 790–803.


