2262
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Pico Canyon Road (WPI). These time-histories were rotated to
their fault-normal/parallel components and only the fault-
normal components were used in the analysis.
3 GROUND MOTION VARIABILITY
Shaking experienced at the hypothetical site was characterized
using published ground motion prediction equations (GMPE)
using a pseudo-probabilistic approach to model variability in the
ground motions. In this approach, the Abrahamson and Silva
(2008) GMPE was used to obtain a median acceleration
response spectrum and the intra-event component of standard
deviation (
) (i.e., single-event variability) for the median
prediction. Variability was modeled by varying the number of
standard deviations (
n
) around the median spectrum (
n
= 0) as
a normally-distributed random variable ranging from
n
= -3 to
+3. The use of a normal distribution achieves symmetry in the
range of
n
generated while preserving the underlying log-
normal distribution of the spectral ordinates. Different target
response spectra were obtained by multiplying
n
by the intra-
event standard deviation and adding or subtracting this from the
medium spectrum. The median,
1
and
3
spectra are
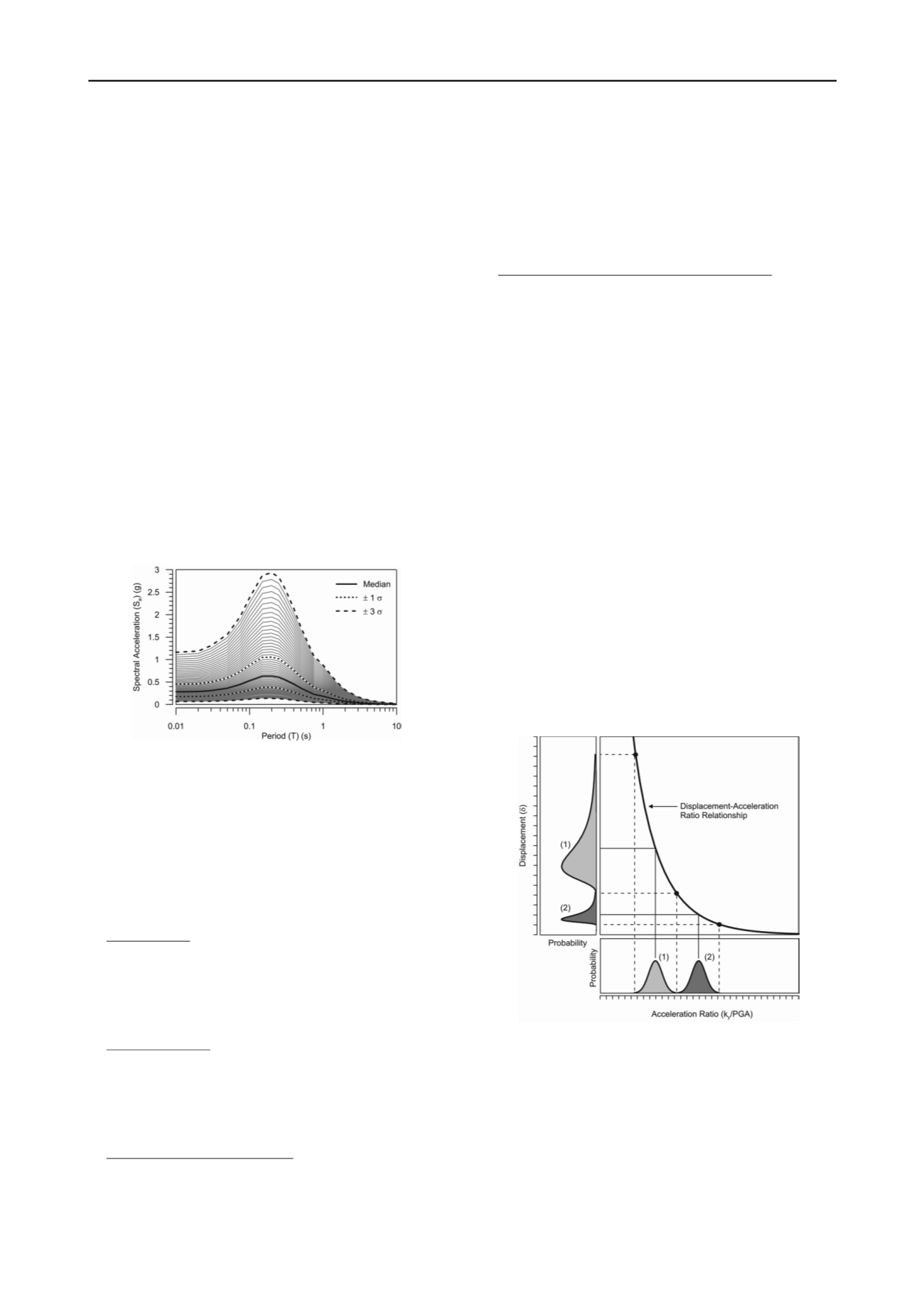
shown in Figure 2; the
PGA
ranges from 0.07 g to 1.15 g with a
median value of 0.28 g. A rock outcropping condition was
simulated by assuming a shear wave velocity over 30 m (
v
s30
) of
1100 m/s and depth of rock of 0 m (ground surface).
Figure 2. Illustration of the range of acceleration response spectra for
the hypothetical site
To understand how ground motion variability affects the
displacement uncertainty, the pseudo-probabilistic approach
described above was implemented in the seismic displacement
analysis in a systematic way by performing multiple
probabilistic analyses for four different scenarios. These
scenarios were designed to progressively increase in their
inherent complexity by introducing different types of ground
motion variability to the seismic displacement analysis. The
four scenarios evaluated are described below.
No variability – This is a baseline condition with no
variability where the ground motion is held at a constant
intensity. Each parent motion (LHA, ORR, VAS, WPI) was
spectrally-matched to the median target response spectra
generating four separate motions each with a
PGA
of 0.28 g.
All spectral-matching was performed using a wavelet-based
algorithm developed by Mukherjee and Gupta (2002).
Variable intensity – For this scenario, variability in the
ground motion intensity is introduced. Using the median
spectrally-matched motions from the previous scenario, in this
approach, variation in intensity is modeled by simple uniform-
scaling to the target
3
PGA
values generated from the
pseudo-probabilistic approach. For each parent motion, a suite
of 1000
PGA
-scaled acceleration time-histories were generated.
Variable intensity and frequency – For this case, additional
variability in form of richer ground motion frequency content is
combined with the variation of intensity. This form of
variability was introduced by considering the variation of
spectral acceleration (
S
a
) with period (
T
) provided by the full
target response spectra. Variability in the frequency content is
modeled in an approximate manner through variation of the
spectral shape and bandwidth of the response spectra between
the
3
bounds (Figure 2). This additional variability was
achieved by spectrally-matching a single parent ground motion
to randomly-selected response spectrum between
3
bounds
generated from the pseudo-probabilistic approach. For each
parent motion, 1000 spectra-compatible acceleration time-
histories were generated.
Variable, intensity, frequency and waveform – In this
approach, additional variability is introduced by using all four
parent ground motions in the spectral-matching process. Since
the wavelet-based spectrally-matching algorithm generally
maintains the non-stationary characteristics of the parent
motions, this scenario provides variability in the core
waveforms that are propagated through the displacement
analysis. To accomplish this, randomly selected parent motions
are paired with randomly selected response spectra (between the
3
bounds generated from the pseudo-probabilistic approach)
and spectrally-matched. A total of 1000 spectra-compatible
acceleration time-histories were generated that incorporate all
four parent ground motions.
4 SEISMIC DISPLACEMENT NON-LINEARITY
While the intended purpose of this study is to examine ground
motion variability, Strenk and Wartman (2011) demonstrated
that predictive uncertainty of common seismic displacement
methods is also a function of a slope’s relative degree of
stability. In the context of Newmark’s sliding block analogy,
the stability of a slope with respect to sliding is defined as the
ratio of a slope’s ability to resist sliding (
k
y
) over the peak value
of the earthquake-induced acceleration (
PGA
) and is referred to
as the acceleration ratio (
k
y
/PGA
). For a variety of simplified,
equation-based methods and even more complex decoupled
methods, a highly-nonlinear relationship exists between the
acceleration ratio and displacement (
); this is illustrated in
Figure 3.
Figure 3. Illustration of the relationship linking the position of the
acceleration ratio distribution to displacement prediction uncertainty.
Non-linearity is a consequence of Newmark’s modeling
decision to approximate the physical mechanism of earthquake-
induced displacement after the inherently non-linear dynamic
behavior of a sliding-block system. This inherent non-linearity
manifests itself through the calculation procedure of “double-
integrating” the acceleration time-history in excess of
k
y
(Newmark 1965) to compute the permanent displacement. In a
probabilistic framework, non-linearity was observed to have a
strong influence on how parametric variability (in seismic
resistance and demand) is propagated through the analysis and
can lead to varying degrees of displacement uncertainty (Strenk


