1272
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Les coordonnées du point C sont obtenues en calculant
l’intersection de la droite de décharge avec la surface d’état
limite qui est une ellipse d’équation :
A
2
s
,
cos
tsin
s
p
,
AC
2
B
2
tcos
s
p
,
sin
2
s
p
2
C
2
0
avec
A
2 (sin
cos
)
cos
2
sin
cos
2
2
2
C
A
C
A B
6,0
C
Les notations suivantes sont utilisées :
-
angle entre l’axe
Os
et l’axe principal de
l’ellipse
,
désignant le coefficient de
pression des terres au repos ;
tg
(1
k
0
) /(1
k
0
)
k
0
-
pression de préconsolidation (contrainte moyenne dans un
essai œdométrique
)
s
p
,
La contrainte
régnant dans le massif peut être obtenue en
combinant les équations (1) à (4). Nous obtenons alors :
3
1
)
1(
3
0
0
0
1 0
0
3
k k
k s
p
(5)
p0
pression de consolidation au niveau de la surface du
sol
p
p
1
1
L’expression (5) montre qu’il subsiste des contraintes
horizontales importantes dans les sols.
3 CARACTERISTIQUES MECANIQUES
Dans les sols surconsolidés se pose toujours le choix des
caractéristiques de cisaillement à prendre en compte
.
3.1
Aspect théorique
Lors de la réalisation des déblais, le chemin de contrainte suivi,
fait qu’en premier lieu la résistance au cisaillement mobilisable
est supérieure à la résistance correspondant à l’état critique
(droite de Mohr - Coulomb), mais il est clair que dès que la
surface d’état limite est atteinte, la résistance au cisaillement
chute brutalement en revenant sur la surface d’état critique.
Il faut donc caractériser la courbe d’état limite pour des sols très
surconsolidés
JF Serratrice (ref. 2) a étudié ces surfaces dans les domaines des
très fortes surconsolidations.
3.1.1
Rappel de la méthode
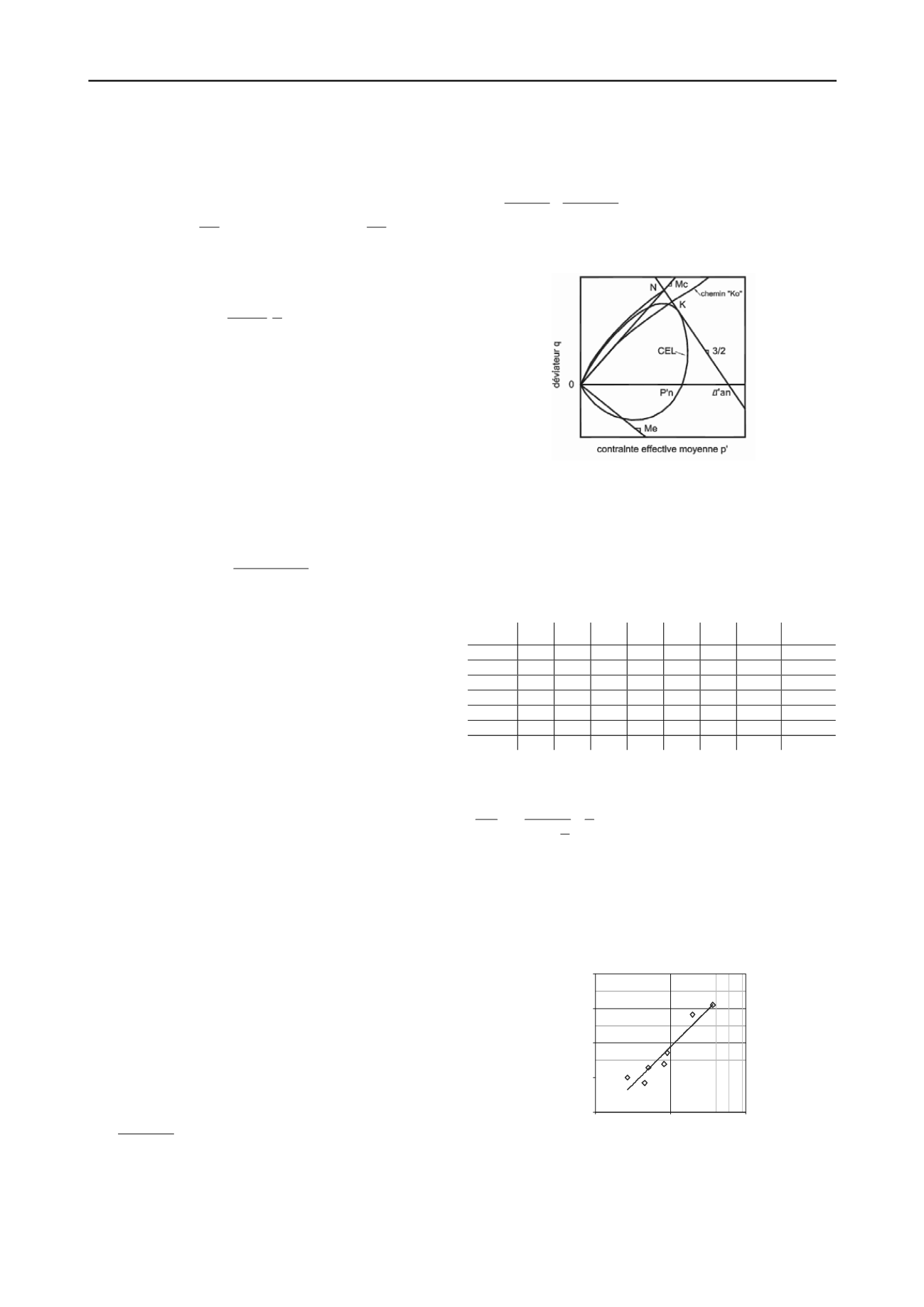
La surface d’état limite à basse pression est tirée du modèle
Camclay avec une représentation par une spirale logarithmique
d’équation
:
,
0
,
,
) /
ln(
pb p p pa q
(6)
avec :
3
2
,
r
a
p
(7)
q
a
r
a
et sont des coefficients positifs
b
La relation (6) n’est valable que pour des basses pressions.
La courbe d’état critique (droite de Mohr-Coulomb) est
représentée par la droite :
q
M
c
p
25
)
(deg
sin 3
sin6
,
,
,
rés
M
c
(8)
Le point d’intersection N a pour coordonnées :(8)
p
0
,
1kPa
(9)
Fig. 3 Représentation de la courbe d’état limite.
Document JF Serratrice
3.1.2
Détermination des paramètres a et b
Dans son article JF Serratrice fournit un tableau donnant les
principaux paramètres des marnes étudiées tableau 1.
Tableau 1 : Données Serratrice
Marn
e
W % e
Mc
’
a
b a/Mc p
n
MPa
3 10,8 0,39 1,18 29,5 0,53 5,68
0,45
5,07
4 24,8 0,68 1,15 28,9 0,43 4,30
0,37
1,51
5 18,0 0,48 1,28 31,8 0,53 5,45
0,41
2,73
6 11,3 0,35 1,30 32,3 0,60 7,25
0,46
19,53
7 14,7 0,40 1,15 28,9 0,45 5,32
0,39
11,06
8 12,0 0,34 1,00 25,4 0,51 5,30
0,51
4,92
9 17,4 0,47 0,86 22,1 0,45 4,43
0,52
2,87
En utilisant les équations (6) à (9) nous obtenons :
a
b
M a
M
c
an
c
2
3
ln
,
(10)
En effectuant une régression linéaire entre b/a et log
an,
nous
avons établi la relation suivante.
b / a
2,17 log
an
2,207
(11)
9,00
10,00
11,00
12,00
13,00
1000
10000
100000
�
an
b/a
Fig 4 Droite de régression
En reportant l’équation (11) dans l’équation (10), il est alors
possible de calculer a puis b.


