1273
Technical Committee 202 /
Comité technique 202
Nous avons appliqué cette méthode à un sol ayant subi 300m
d’érosion
Les caractéristiques géotechniques sont reportées dans le
tableau 2
Tableau 2 : Données du sol étudié
h e (m)
300,00
300,00
z (m)
0,00
40,00
an
(kPa)
6300
7140
p
n
(kPa)
2405
2725
lnp
n
8,1906
8,3158
b/a
10,45
10,57
M
c
1,12
1,12
M
c
/a
2,26
2,26
a
0,49
0,50
b
5,17
5,25
A partir des données du tableau 2 nous avons déterminé la
courbe d’état limite en surface et à une profondeur de 40m dans
l’espace
p;q
Fig 5 Courbe d’état limite
Du fait de la forte surconsolidation la courbe d’état limite varie
peu avec la profondeur.
3.2
Détermination des caractéristiques mécaniques
Les modèles décrits dans les paragraphes précédents montrent
que la stabilité d’un talus dépend :
de la surface d’état limite en premier lieu ;
de la courbe de rupture de Mohr- Coulomb
étant, bien entendu, que dès que l’état de contrainte touche la
surface, il y a rupture.
Pour ce qui concerne les caractéristiques mécaniques de Mohr-
Coulomb, elles sont caractérisées par un angle de frottement
et une cohésion qui est telle que
.
,
c
,
0
Nous allons étudier plus avant la surface d’état limite pour la
modéliser simplement.
3.2.1
Représentation de la SEL dans l’espace s, t
A partir de l’espace p,q, nous avons calculé la surface d’état
limite dans l’espace s, t, qui représente le lieu des sommets des
cercles de Mohr.
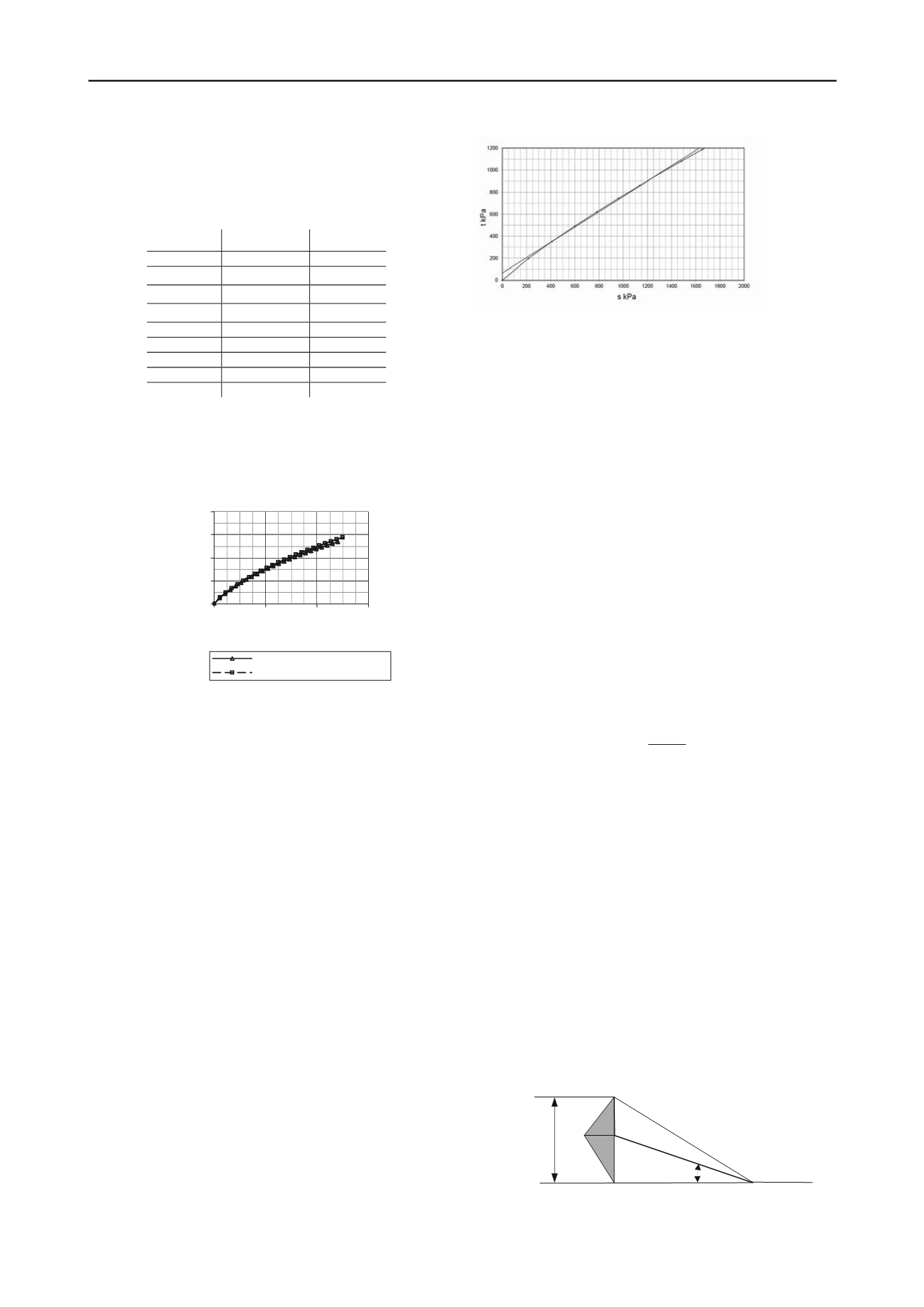
Nous constatons que dans le domaine des basses pressions la
surface d’état limite Fig 6 peut être représentée par deux droites.
Fig 6 : Courbe d’état limite espace s, t
Les notations utilisées sont les suivantes :
l’angle de frottement est noté
,
la cohésion
t
0
Ces droites ont été obtenues par régression linéaire.
La première droite passant par l’origine a pour caractéristiques :
tg
,
0,86
kPa
t
68,3
,
0
Pour la seconde nous obtenons :
tg
,
0,70
kPa
t
65
,
0
0
1000
2000
3000
4000
0
1000 2000 3000
p kPa
3.2.2
Caractéristiques mécaniques de cisaillement
q kPa
o
État critique
D’après le Tableau 2,
, il en résulte
, la
cohésion quant à elle, est quasiment nulle
M
c
1,12
,
28
c
,
0
o
Surface d’état limite
Nous avons vu qu’elle pouvait être décomposée en deux droites.
Le passage des caractéristiques déterminées dans l’espace (s,t) à
l’espace (
,
) dans lequel la droite de Mohr- Coulomb est
définie par
’ et c’, s’effectue avec les relations de passage
suivantes :
presson consolidation=6300kPa
pression consolidation=7140kPa
sin
,
tg
,
,
0
,
cos
t
c
Nous obtenons donc :
Première droite passant par l’origine
,
59
,
kPa
c
8
Deuxième droite
,
44
Ces deux droites se coupent pour une contrainte :
c
,
91kPa
122kPa
soit une hauteur de sol
m h
80,5
4
MÉTHODE DE CALCUL
4.1
Choix de la méthode
Pour montrer l’influence des contraintes, nous avons choisi une
méthode de calcul par bloc pour pouvoir prendre en compte les
efforts horizontaux dus à la surconsolidation, ce qui n’est pas
possible dans les autres méthodes.
Fig 7 : schéma de calcul de stabilité
F
0
A E H


