1268
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
a
s
x
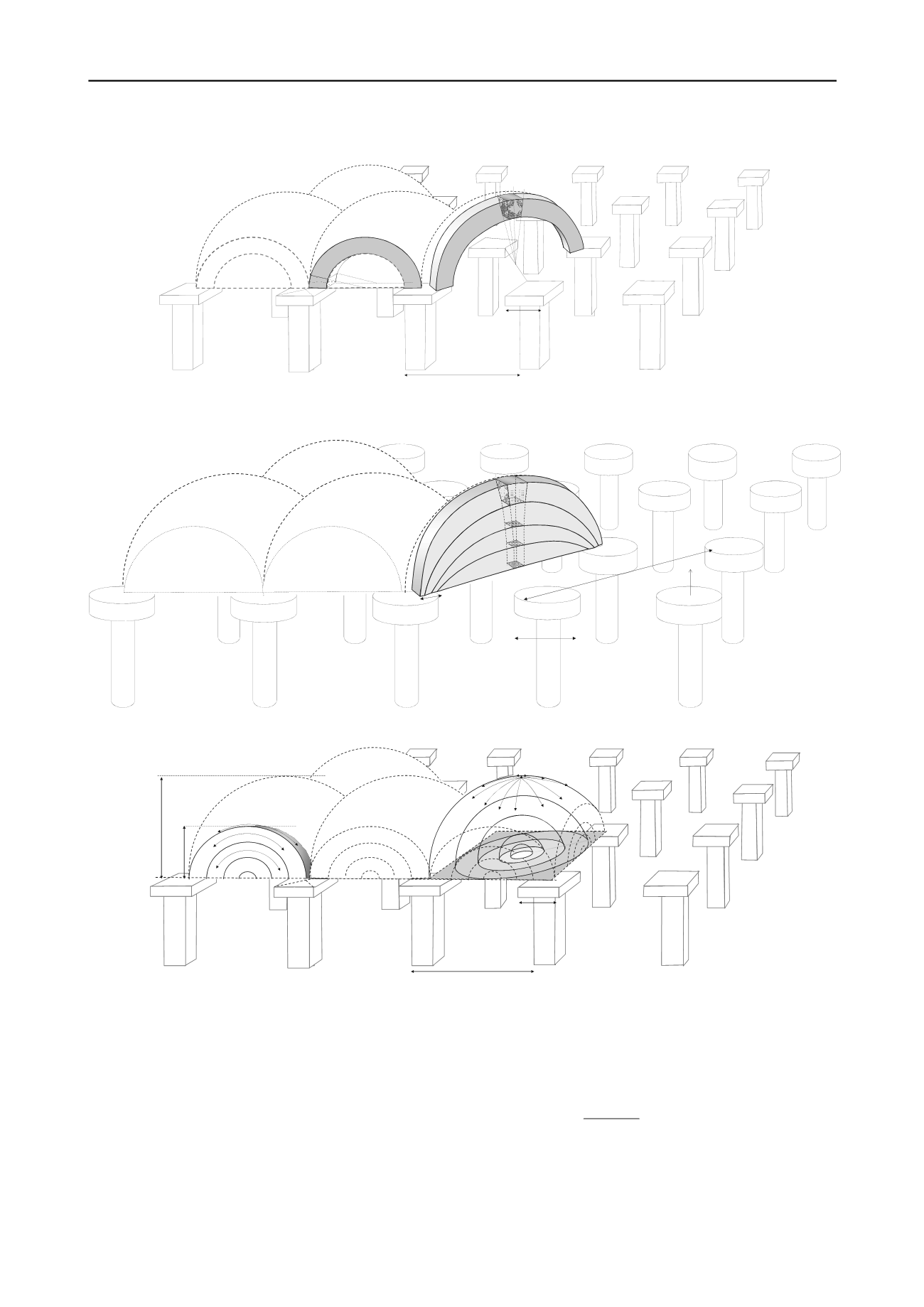
Figure 2. Hewlett & Randolph (1988) consider the ‘crown’ element of the diagonal arch and the ‘toe’ element (just above the pile cap) of the plane
strain arch as indicated in this figure.
s
d
d
d/2
z
Figure 3. Zaeske (2001) considers the equilibrium of the crown elements of the diagonal arches
s
x
a
H
g3D
H
g2D
Figure 4. Van Eekelen et al. (2013b), the Concentric Arches Model. The load is transferred along the 3D hemispheres (right hand side) towards the GR
strips and then via the 2D arches (left hand side) towards the pile caps
A third model is the concentric model presented by Van
Eekelen et al. (2013b). Figures 2 to 4 present these three models
and are presented in the following sections.
3 HEWLETT AND RANDOLPH (1988)
Hewlett & Randolph (1988) based their model on 3D door trap
tests, without geosynthetic reinforcement. Their analytical
model consists of a series of thick-walled 3D-shells, or arches,
in the embankment. They consider two arch elements
separately: a ‘crown element’ and an element just above the pile
cap, the ‘toe’ element, as shown in Figure 2 and Figure 5. For
the toe element, the pile load (
A
) is calculated by assuming
radial equilibrium of the crown element in the plane strain arch
(left in Figure 2) and assuming that the principal stresses follow
the arches with
the major principal stress and
r
the minor
principal stress and that the arches are in a nearly-plastic
situation:
1 sin
1 sin
p r
K
r
(1)
Where
(kPa) is the tangential stress,
r
(kPa) is the radial
stress,
K
p
(-) is the Rankine passive earth pressure coefficient
and
(
o
) is the friction angle. The pile load (A) is obtained by
integrating
over the pile area, indicated in Figure 5. For the
crown element, the vertical stress
r;i
below the crown is
calculated using equilibrium of the crown element in the 3D


