1281
Technical Committee 202 /
Comité technique 202
Cote par rapport à la base du
F
igure 3. Aperçu en coupe des contraintes principales au sein d’un
remblai de 1 m de haut renforcé par un géosynthétique de raideur
3000 kN/m, sur une cavité de 1,1 m de rayon.
4 CONFRONTATION ENTRE RÉSULTATS
EXPÉRIMENTAUX, ANALYTIQUES ET NUMÉRIQUES
4.1
Outils d’analyse analytique
La méthode analytique utilisée à titre de comparaison avec
les résultats expérimentaux et numériques a été établie par
Villard et Briançon (2008) pour les remblais granulaires non
cohésifs. Le problème est considéré en deux dimensions
(déformations planes). Le géosynthétique est renforcé dans la
direction longitudinale (le sens du trafic) et son comportement
en tension est décrit par une loi linéaire élastique : T = J.
, où T,
J et
sont respectivement la tension, la raideur et la déformation
de la nappe. Le comportement d’interface entre le renforcement
et le sol est régi par une loi de frottement élastique-plastique de
Coulomb. La non linéarité du comportement du géosynthétique
peut être grossièrement approchée en utilisant une raideur
sécante calculée dans la section de nappe la plus sollicitée.
La distribution des contraintes sur le géosynthétique au droit
de la cavité et en zone d’ancrage est supposée uniforme. Trois
mécanismes sont pris en compte pour le dimensionnement : la
mobilisation du frottement en zone d’ancrage, l’effet membrane
au droit de la cavité, et le changement d’orientation de la nappe
sur le bord de la cavité.
4.2
Flèche du renforcement géosynthétique
Les Figures 4 et 5 illustrent les déplacements verticaux des
géosynthétiques sur les plots GR1 et GR2 après ouverture de la
cavité à 2,2 m de diamètre. Ces données sont estimées
numériquement ou analytiquement, ou calculées à partir des
mesures expérimentales de positionnement du géosynthétique
au radar géologique. On note que les mesures expérimentales au
radar géologique ont donné lieu à une interprétation minutieuse
des données dont la précision est toutefois estimée à ± 2 cm. A
partir de la déformée de la nappe géosynthétique et des
déflexions de surfaces on peut estimer le coefficient de
foisonnement du sol à environ 1.03 sur les deux plots.
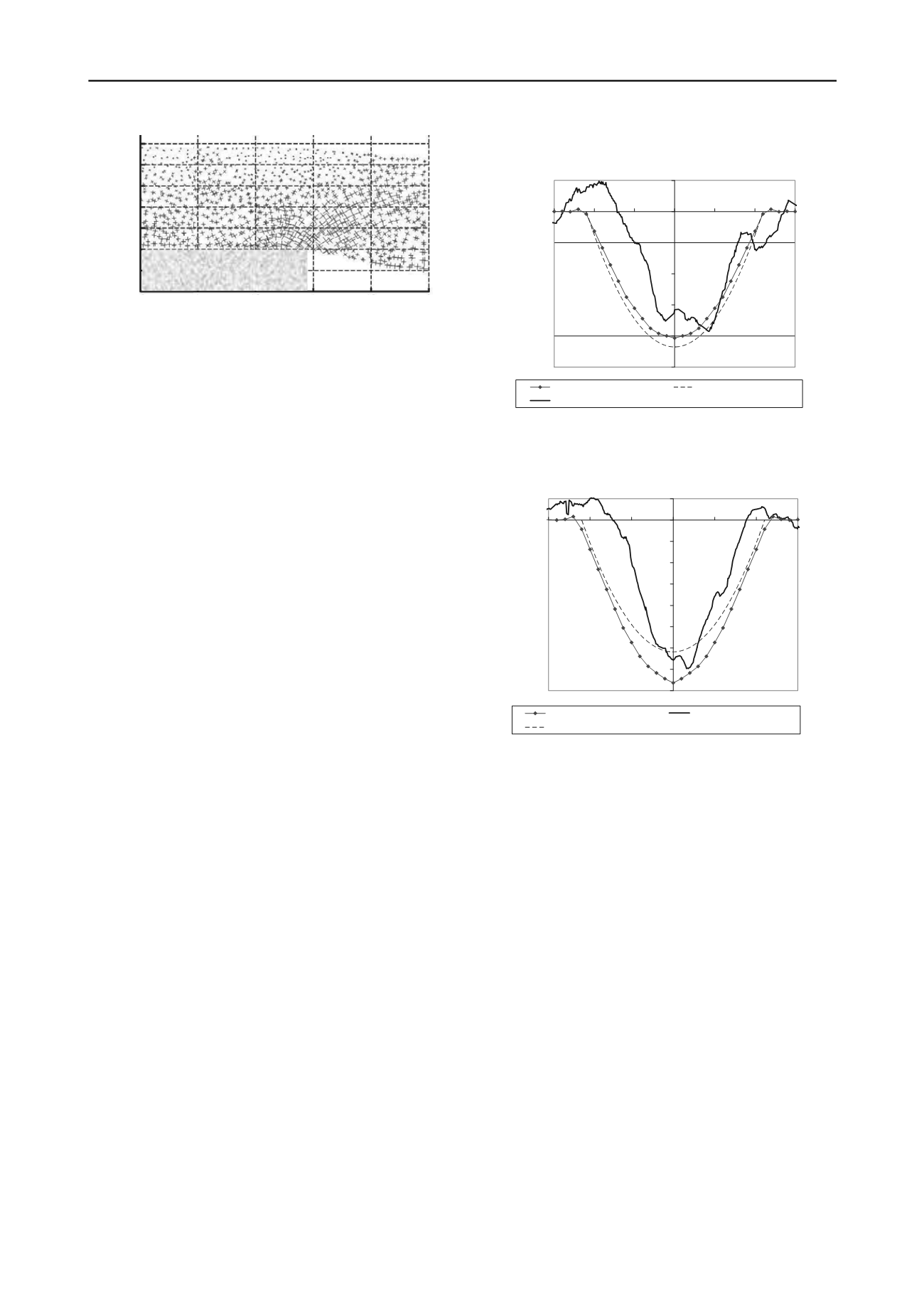
En règle générale (Figures 4 et 5) pour une cavité de 2,2 m
de diamètre, les ordres de grandeur des flèches des
géosynthétiques sont assez semblables que l’on considère les
résultats expérimentaux, numériques ou analytiques. Les
résultats obtenus sont une flèche numérique de 20,3 cm pour
une flèche analytique de 21,7 cm et une mesure expérimentale
de 20 cm environ sur le plot GR1. Sur le plot GR2, l’estimation
numérique de la flèche est de 38,2 cm pour un calcul analytique
de 30,9 cm et une mesure expérimentale de 35 cm environ.
On constate (Figures 4 et 5) que les courbes expérimentales
sont légèrement décalées par rapport aux courbes numériques et
analytiques. Les mesures expérimentales ayant été effectuées en
conditions de chantier, les profils de mesure peuvent être
légèrement désaxés, ce qui expliquerait les différences entre
flèches numériques, analytiques et expérimentales observées sur
les plots GR1 et GR2.
Figure 4. Plot GR1 – Déplacements verticaux du géosynthétique après
ouverture de la cavité.
Figure 5. Plot GR2 – Déplacements verticaux du géosynthétique après
ouverture de la cavité.
En comparant les résultats analytiques et numériques sur le
plot GR1, on constate que la méthode analytique utilisée permet
une bonne estimation des valeurs de déflexions de la nappe. Les
différences constatées avec les résultats numériques peuvent
s’expliquer par une mauvaise prise en compte des mécanismes
de reports de charge dans la méthode analytique (hypothèse
d’une charge uniformément repartie) qui peuvent être plus
complexes dans la réalité. Sur le plot GR2 les écarts entre les
résultats analytiques et numériques sont plus prononcés. Une
explication est que la méthode analytique suppose un
comportement linéaire du géosynthétique (ou l’utilisation d’un
module sécant approchant) alors que le modèle numérique tient
compte de manière très réaliste du comportement non linéaire.
4.3
Déformation du renforcement géosynthétique
Une comparaison des mesures expérimentales de déformation
de la nappe géosynthétique par fibre optique avec les résultats
de déformation des simulations numériques et des calculs
analytiques est présentée sur la Figure 6. On constate pour le
plot GR1 (Figure 6) que les mesures expérimentales effectuées
sur une cavité de 2,2 m de diamètre sont bien corrélées aux
prédictions numériques. Les résultats du calcul analytique se
corrèlent également assez bien aux résultats expérimentaux en
zone d’ancrage. En revanche, au droit de la cavité, les
déformations analytiques sont supérieures aux valeurs
numériques et expérimentales, ce qui reste logique puisque la
flèche analytique est plus importante sur le plot GR1 (Figure 4).
max
= 30 kPa
1
-0,05
0,00
0,05
0,10
0,15
0,20
0,25
-1,5 -1,0 -0,5 0,0 0,5 1,0 1,5
Abscisse linéique par rapport au centre de la cavité (m)
Flèche du géosynthétique selon calcul
numérique ou radar de sol (m)
Numérique - D=2,2m
Analytique - D=2,2m
Expérimental - D=2,2m
0,8
0,6
0,4
0,2
remblai (m)
0
-0,2
Abscisse linéique par rapport au centre de la cavité (m)
-2,5
-2
-1,5
-1
-0,5
0
-0,05
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
-1,5 -1,0 -0,5
0,0
0,5
1,0
1,5
Abscisse linéique par rapport au centre de la cavité (m)
Flèche du géosynthétique selon calcul
numérique ou radar de sol (m)
Numérique - D=2,2m
Expérimental - D=2,2m
Analytique - D=2,2m


