779
Technical Committee 103 /
Comité technique 103
corresponding to the beginning of the shear phase. Five tests were
performed under this constant suction, having different confining
pressures: 4 MPa (tests 3 and 4), 8 MPa (tests 6 and 8), and
12 MPa (test 12) (Muralha et al. 2011). Only test 12 is analysed in
this paper because it differs from the others due to the fact that
one unloading / reloading cycle was applied in shear phase. This
cycle is important to characterise the shear stiffness in the elastic
range necessary for the constitutive model. The curves
corresponding to the two loading stages are shown in Figure 2.
For this test
12 MPa
at the beginning of the shear phase.
4 MODEL CALIBRATION
The parameters for the constitutive model were determined by
fitting the experimental results found in test 12 using a GA and
a HC procedure implemented in MATLAB. The constitutive
model was implemented in FLAC.
Figure 2. Experimental data of the test 12 defined in total stresses: a)
isotropic phase, b) and c) shear phase.
Figure 3. Scheme for implementing HC procedure into the GA in
MATLAB with the numerical simulations in FLAC.
Table 1. Limits of the search area of each parameter.
Parameter
Max
Min
Parameter
Max
Min
κ
0.007
0.002
ρ
3.0
0.0
λ
0.030
0.008
p
cb,ini
8000
3000
Μ
1.85
1.20
b
ini
3.0
0.0
ν
0.35
0.25
α
ini
0.5
0.0
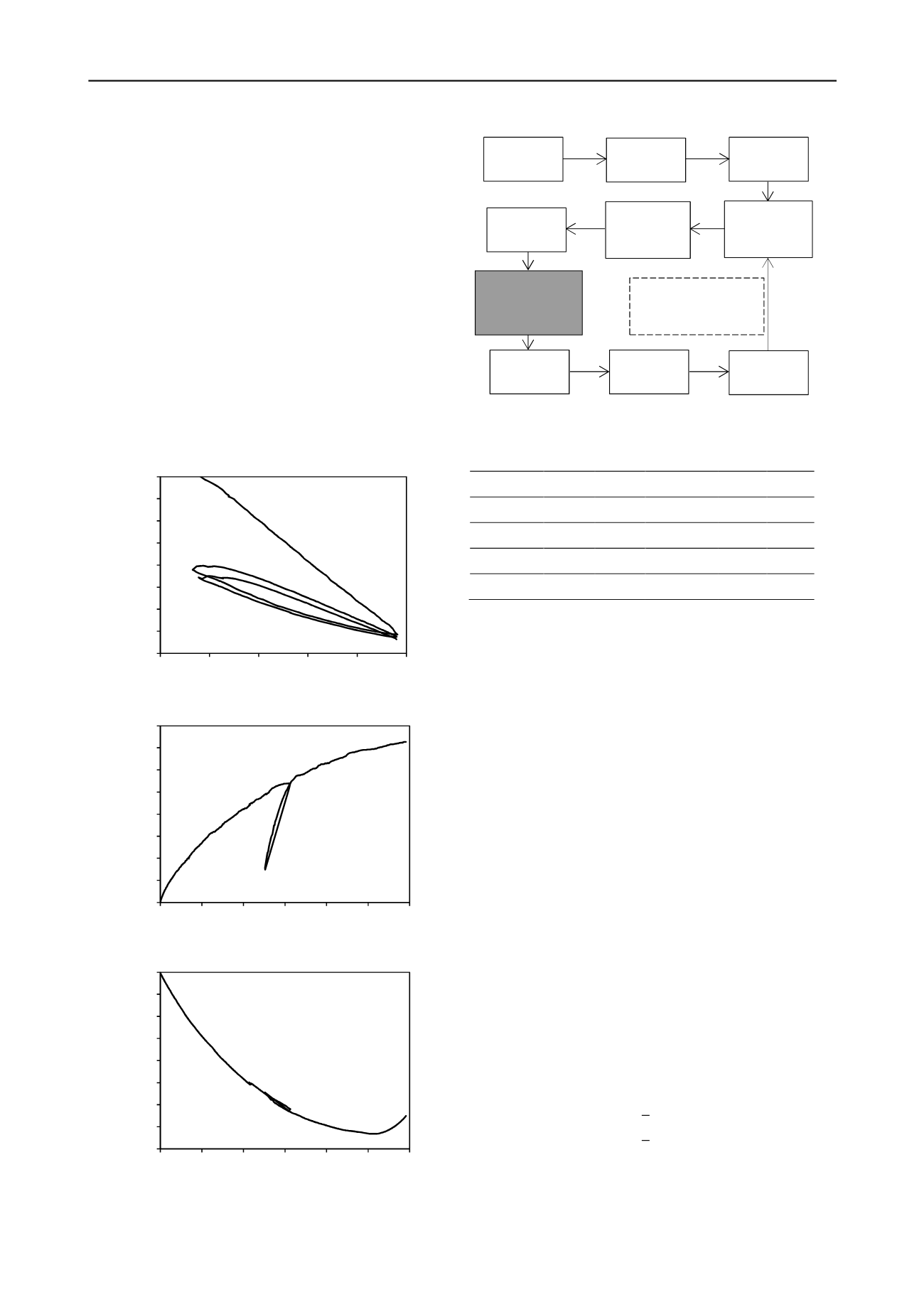
GA are assumed to be global search methods used to solve
optimisation problems (see Pal et al. 1996). They employ
concepts from the theory of natural evolution, such as selection,
mutation, inheritance and crossover. HC procedure is a local
direct search optimisation technique which, starting from a
given initial solution, attempts to improve it by randomly
altering its characteristics. The linkage between GA and HC
was done according to the recommendations presented in
Renders and Bersini (1994) and Taborda et al. (2011).
A simplified diagram illustrating the implementation process
is presented in Figure 3. The algorithm starts with the definition
of the initial population. For this problem, the initial population
was randomly generated and was composed by 256 individuals.
Each individual had 8 parameters (8 genes), which are the
parameters of the model previously defined. In fact they should
be 9 parameters but
was considered to be zero because the
experimental curves measured in the shear phase tended to a
horizontal line (Figure 2b and c). The limits of the search area
of each parameter are presented in Table 1. The limits of
ensure
,
>
,
(Eq. 8).
Mutation, usually introduced in GA methods to avoid their
early convergence into a unique solution, is replaced by
coupling HC to GA because HC modifies the genes in each
iteration.
The numerical simulation of each individual was performed
by FLAC with the purpose to reproduce test 12 in both isotropic
compression and shear stages. The unloading / reloading cycles
from the two stages were considered.
The evaluation of each individual was made by measuring
the area between the numerical and the experimental curves
defined in spaces (i)
−
, (ii)
−
and (iii)
−
, where
= 2 3 ‖‖
(19)
represents the deviatoric strain. The results were considered on
dimensionless spaces to avoid scale effects. The 25% best
individuals were selected to the next iteration.
0
2
4
6
8
10
12
14
16
0.0
2.5
5.0
7.5
10.0 12.5
∆
ε
v
(10
-3
)
p
(MPa)
0
5
10
15
20
25
30
35
40
0
5
10
15
20
25
30
q
(MPa)
∆
ε
q
(10
-3
)
0
2
4
6
8
10
12
14
16
0
5
10
15
20
25
30
∆
ε
v
(10
-3
)
∆
ε
q
(10
-3
)
b)
c)
a)
Initial
population
Numerical
simulation
Evaluation
of fitness
Selection of
the 25% best
individuals
Generation
of 25% new
individuals
Crossover
Mutation (not
applied in this
paper)
Numerical
simulation
Evaluation
of fitness
Hill
Climbing
Perform new iteration
until exit criterion is
satisfied


