783
Technical Committee 103 /
Comité technique 103
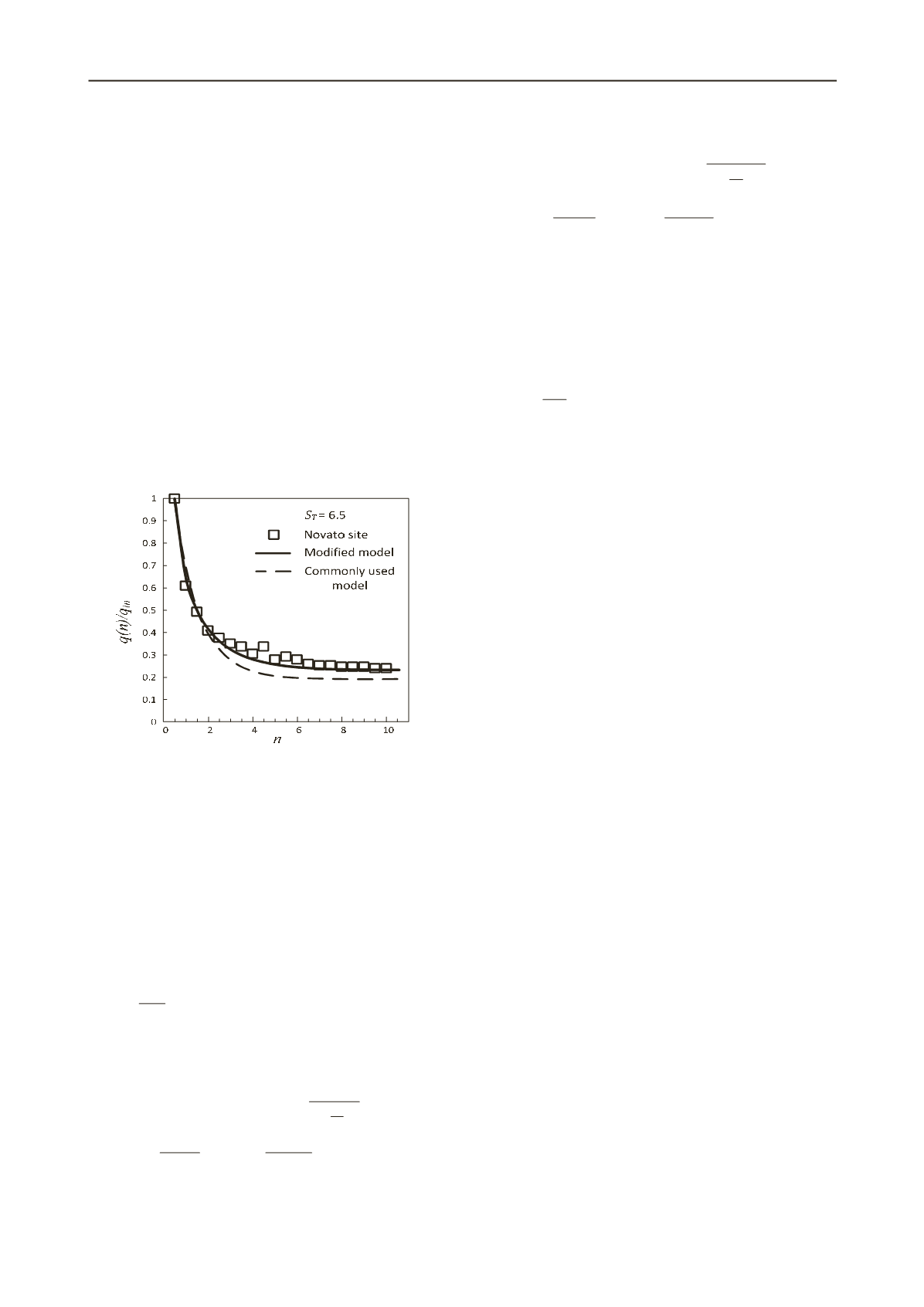
Fig. 3 shows the agreement between the results obtained using
the new softening model (Pinkert, 2012) and the commonly
used softening model, for one of the examined test sites
reported by Yafrate et al. (2009). Similar agreement was
obtained for the other sites. This degradation model is later used
in the creation of a general expression for engineering use.
3.3. Anisotropy effect:
Klar and Pinkert (2010) examined the effect of soil anisotropy.
In this specific problem the resistance is also affected by the
rigid body rotation which soil elements experience through the
penetration process. Two models of anisotropy were considered:
[a] in which the anisotropy ratio remain constant with
degradation, and [b] in which the anisotropy ratio diminishes
with increasing cumulative shear strains. It was found that if an
“average” undr
ained shear strength value (i.e. average of the
undrained shear strengths measured in the horizontal and the
vertical directions) is used in the normalization of the resistance
factor, the effect of anisotropy is minimal. Consequently, the
measured penetration resistance may only indicate on the
average strength.
Figure 3. Normalized cyclic penetration resistance results for each
cycle,
n
, of the (1) experimental results, (2) the numerical results using
the commonly used stain softening model and (3) the numerical results
using the new strain softening model.
4 ALGEBRAIC EXPRESION FOR ENGINEERING USE
The above trends and solutions were unified to result in a single
algebraic expression, which was calibrated using the topological
ordering based upstream weighting method developed by Klar
and Pinkert (2010). The range of calibration corresponds to
*
≤0.15
,
S
T
≤50
and 0.05
≤
v
/
d
≤12.5
. For engineering use, the
undisturbed undrained shear strength,
s
u0
, may be evaluated as
follows:
i
u
AN
P s
0
(8)
where
P
is the measured penetration force,
A
is the projected
area of the penetrometer, and
N
i
is the resistance factor for T-
bar and ball as given by:
ref
S
T
ref
Tbar
Tbar
dv
dv
S
N
N
T
/
/
log
1
51
5.4
1
1
114 .0
log 22.01
*
*
*
1
7
15
,
1
(9)
ref
S
T
ref
ball
ball
dv
dv
S
N
N
T
/
/
log
1
51
2.4 1
1
438 .0
log 55.01
*
*
*
2
8.1
11
,
2
(10)
where
N
Tbar,ref
=11.98 and
N
ball,ref
=15.23, which relate to the
conventional penetration velocity and penetrometer geometry,
for a non-viscous soil. (
v
/
d
)
ref
is equal to 0.5 for T-bar and 0.18
for ball. The parameter
*
may be evaluated from at least two
test results, at different
v
/
d
ratios, according to Eq. 3 and the
value of
S
T
can be evaluated using the first insertion and first
extraction of the penetrometer (Yafrate et al., 2009):
7.3
out
in
T
q
q
S
(11)
where
q
in
and
q
out
are the penetration resistances (=
P
/
A
) at the
first insertion and extraction, respectively, in a cyclic
penetration test.
5 CONCLUSIONS
The paper utilizes an advance numerical approach, which is
calibrated using field experimental tests results, to produce a
unified expression for the evaluation of the undrained shear
strength from
“
full-flow
”
penetrometers (T-bar and ball). The
resulting expressions may be used for determination of the soil
undrained strength value, by a set of minimum two tests, one
cyclic and the other under different penetration rate.
6 REFERENCES
Dayal U. and Allen J.H. 1975. Effect of penetration rate on strength of
remolded clay and sand samples.
Canadian Geotechnical Journal
12 (3), 336
–
348.
Einav I. and Randolph M. 2005. Combining upper bound and strain path
methods for evaluating penetration resistance.
International
Journal for Numerical Methods in Engineering
63 (14), 1991-2016.
Klar A. and Osman A. S. 2008. Continuous velocity fields for the T-bar
problem.
International Journal for Numerical and Analytical
Methods in Geomechanics
32, 949
–
963.
Klar A. and Pinkert. S. 2010. Steady state solution for cylindrical
penetrometers.
International Journal for Numerical and Analytical
Method in Geomechanics
34, 645-659.
Pinkert S. 2012. Solution of steady state plastic flow problems in
saturated clays,
PhD dissertation
, Technion - ITT, Israel.
Randolph M. F. 2004. Characterisation of soft sediments for offshore
applications. Proc. 2nd Int. Conf. on Site Characterisation 1, 209
–
231, Porto.
Randolph, M.F. 2012. Offshore Geotechnics
–
the Challenges of
Deepwater Soft Sediments. ASCE Geotechnical Special Publication
No. 226: Geotechnical Engineering State of the Art and Practice:
Keynote Lectures from GeoCongress 2012. 241-271.
Yafrate N. J. and DeJong J. T. 2007. Influence of penetration rate on
measured resistance with full-flow penetrometers in soft clay.
In
New Peaks in Geotechnique
, GeoDenver. Denver. US.
Yafrate N.J.,
DeJong J.T.,
Degroot
D.
and Randolph
M.F. 2009. Evaluation of remolded shear strength and sensitivity of
soft clay using full flow penetrometers.
Journal of Geotechnical
and Geoenvironmental Engineering
135 (9), 1179-1189.
Zhou H. and Randolph M.F. 2007. Computational techniques and shear
band development for cylindrical and spherical penetrometers in
strain-softening clay.
International Journal of Geomechanics
7(4),
287-295.
Zhou H. and Randolph M. F. 2009. Numerical investigations into
cycling of full-flow penetrometers in soft clay.
Geotechnique
59(10), 801
–
812.


