778
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
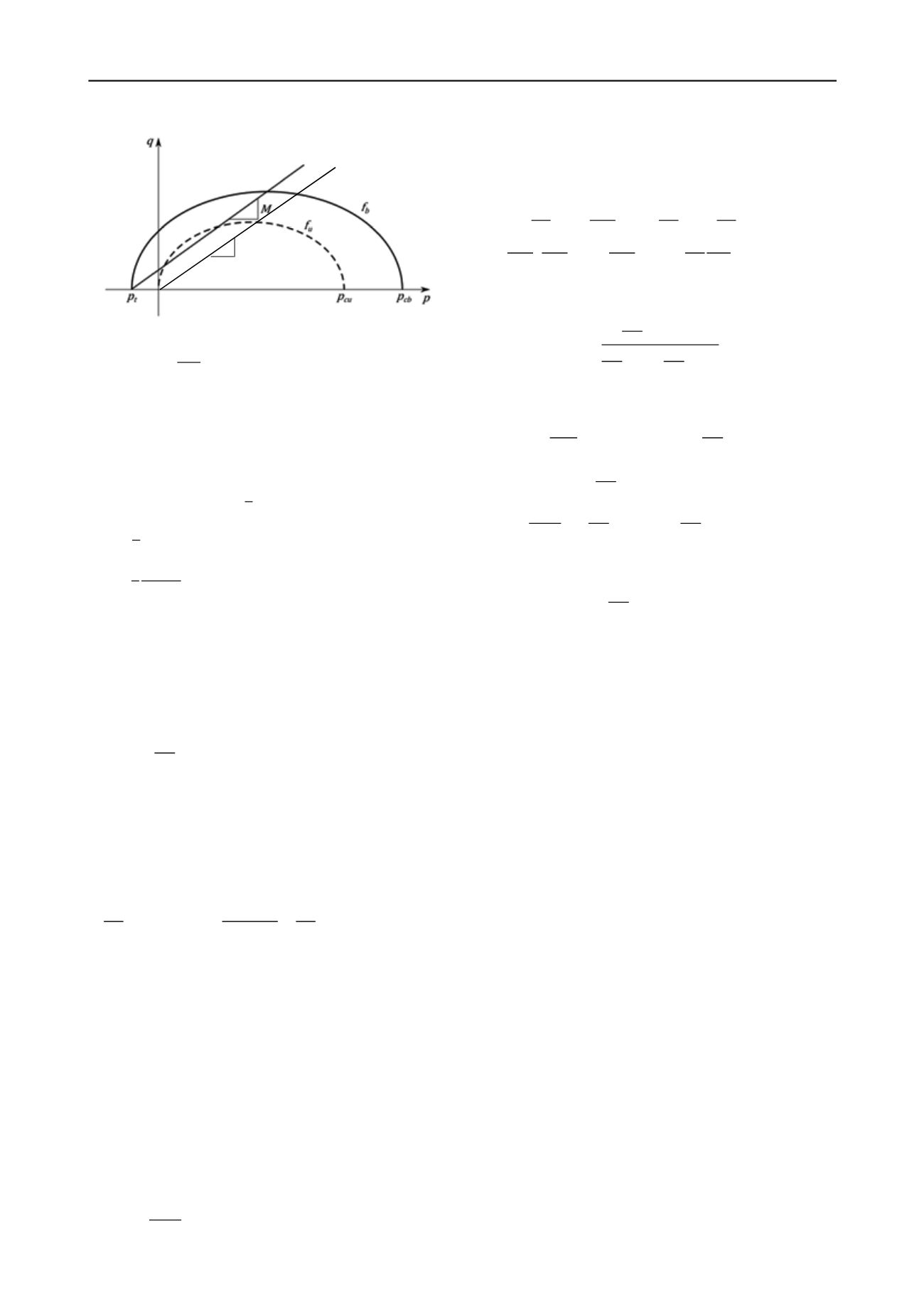
Figure 1. Representation of the model’s yield surfaces, in a (
p
,
q
) space.
When
= 2 3⁄
, the modified Cam Clay yield surface is
obtained for
. The two yield surfaces concept follows the
work presented by Gens and Nova (1993).
The elastic behaviour is governed by the following
hypoelastic model
d
∶ d
d
2d
(3)
⊗ 2 1 3 ⊗
(4)
(5)
3 2 1 2 1
(6)
where
d
is the increment of the elastic effective stress tensor,
the fourth order elastic stiffness tensor,
and
the elastic
bulk and shear modulus, respectively,
the Poisson’s ratio,
d
the elastic volumetric strain increment,
d
the deviatoric part of
the elastic strain tensor increment and
the swelling lines slope.
An associated plastic flow law is considered. Therefore, the
plastic strain rate,
d
takes the form
d
Λ
(7)
where
Λ
is the plastic multiplier.
This model has two hardening laws: (i) the first one is
related with the behaviour of the unbonded yield surface,
,
and (ii) the second one is related with the decrease of the space
between both yield surfaces as a result of debonding.
Based on the work presented by Nova (2005), the bonding
effects can be quantified by a parameter
b
, defined as
1 ⇔
,
(8)
and the value of
is defined as
(9)
where
represents the part of the yield mean
stress corresponding to the bond effects and
defines the value
of
as a function of
.
According to the same author, the hardening laws of the
and
take the form of Eqs. 10 and 11, where parameter
depends on the bond fragility, since it measures the rate at
which the bonds are broken and the soft rock is transformed into
a destructured soil,
is the normal compression line slope of
the unbounded material,
controls the value of dilatancy at
failure,
d
is the plastic volumetric strain increment and
d
is
the deviatoric part of the plastic strain tensor increment.
d
d
‖d
‖
(10)
d
d
(11)
Through the consistency condition, defined as
d
: d
d
d
: d
d
d
d
0
(12)
the plastic multiplier,
Λ
, is obtained by
Λ
∶
∶ d
∶
∶
(13)
with
1
(14)
tr
(15)
tr
dev
.
(16)
The increment of the effective stress tensor,
d
, is defined as
d
∶ d Λ
.
(17)
This constitutive model requires the definition of nine
parameters: six constants (
,
,
,
,
and
) and three initial
values (
,
,
,
and
), in addition to the initial stress
and strain tensor,
and
, respectively.
3 MARL’S PROPERTIES AND EXPERIMENTAL TESTS
An extensive set of experimental tests was performed to
characterise the behaviour of the marls studied in unsaturated
states (Cardoso 2009, Muralha et al. 2011). The tests performed
on rock specimens for characterising the mechanical properties
of this marl are unconfined compression tests, Brazilian splitting
tests, oedometric tests and isotropic compression tests followed
by triaxial tests. Unsaturated states were achieved using vapour
equilibrium as controlled suction technique (Cardoso, 2009).
Only the results of the triaxial tests performed under constant
suction
39 MPa
(
75%
) are analysed in this paper.
The model adopted was used to this unsaturated material
after computing effective stresses using Eq. 18 proposed by
Alonso et al. (2010)
′
(18)
where,
′
is the effective stress tensor,
the net
stress tensor,
the total stress tensor,
the air pressure,
s
the
suction,
the degree of saturation and
the parameter that
corrects the global degree of saturation to discount the
microstructural degree of saturation, which quantifies the
immobile water within the soil that does not affect volume
changes. For
39 MPa
,
35%
considering the water
retention properties of the marls determined by Cardoso (2009).
For this material
4.56
. Assuming
0
,
325.1 kPa
.
The stress paths adopted in these tests consisted of a first stage
where isotropic compression was applied, followed by the
increment of the axial stress until shear failure. Two
unloading / reloading cycles were applied in the isotropic
compression phase under the confinement mean stress
M


