2681
Technical Committee 212 /
Comité technique 212
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
1
1
2
2
1
1
1
2
2
1
1
1
8
2
i
i
i
i
H n
pi
n
si
sn pn z
i
n
H
p
H n
p
n
si
pi
sn pn z
i
n
H
d
k
G
dz G
dz
t
r
L
t
G dz G
k
At the boundaries
r = r
p
and
r =
,
s
is prescribed as
s
= 1
and
s
= 0, respectively, which form the boundary conditions of
equation (13).
(14)
The solution of equation (13) subjected to the above
boundary conditions is given by
1
1
p
s
K r
r
K
where
K
1
(
) is the first-order modified Bessel function of the
second kind. The dimensionless parameter
determines the rate
at which the displacement in the soil medium decreases with
increasing radial distance from the pile.
(15)
Equations (3) and (15) were solved simultaneously
following an iterative algorithm because the parameters
involved in these equations are interdependent. At the same
time, adjustments were made to the shear modulus by replacing
G
s
by an equivalent shear modulus
*
0.5
s
s
G
G
. This was
necessary because the assumed soil displacement field
described in equation (1) introduced artificial stiffness in the
system and replacing
G
s
by
G
s
*
reduced this stiffness.
3 RESULTS
The accuracy of the proposed analysis is checked by comparing
the results of the present analysis with those of previously
obtained analyses and of three-dimensional (3D) finite element
analyses performed as a part of this study. In order to compare
the results with those of the existing solutions, normalized angle
of twist at the pile head
I
(also known as the torsional influence
factor) and relative pile-soil stiffness
t
(Guo and Randolph
1996) are defined for piles in homogeneous soil deposits (with a
constant shear modulus
G
s
)
0
0
p
p p
z
p z
a p
a
G J
I
T L
T
(16)
1
2
2
4
p s
t
p
p p
r G
L
G J
(17)
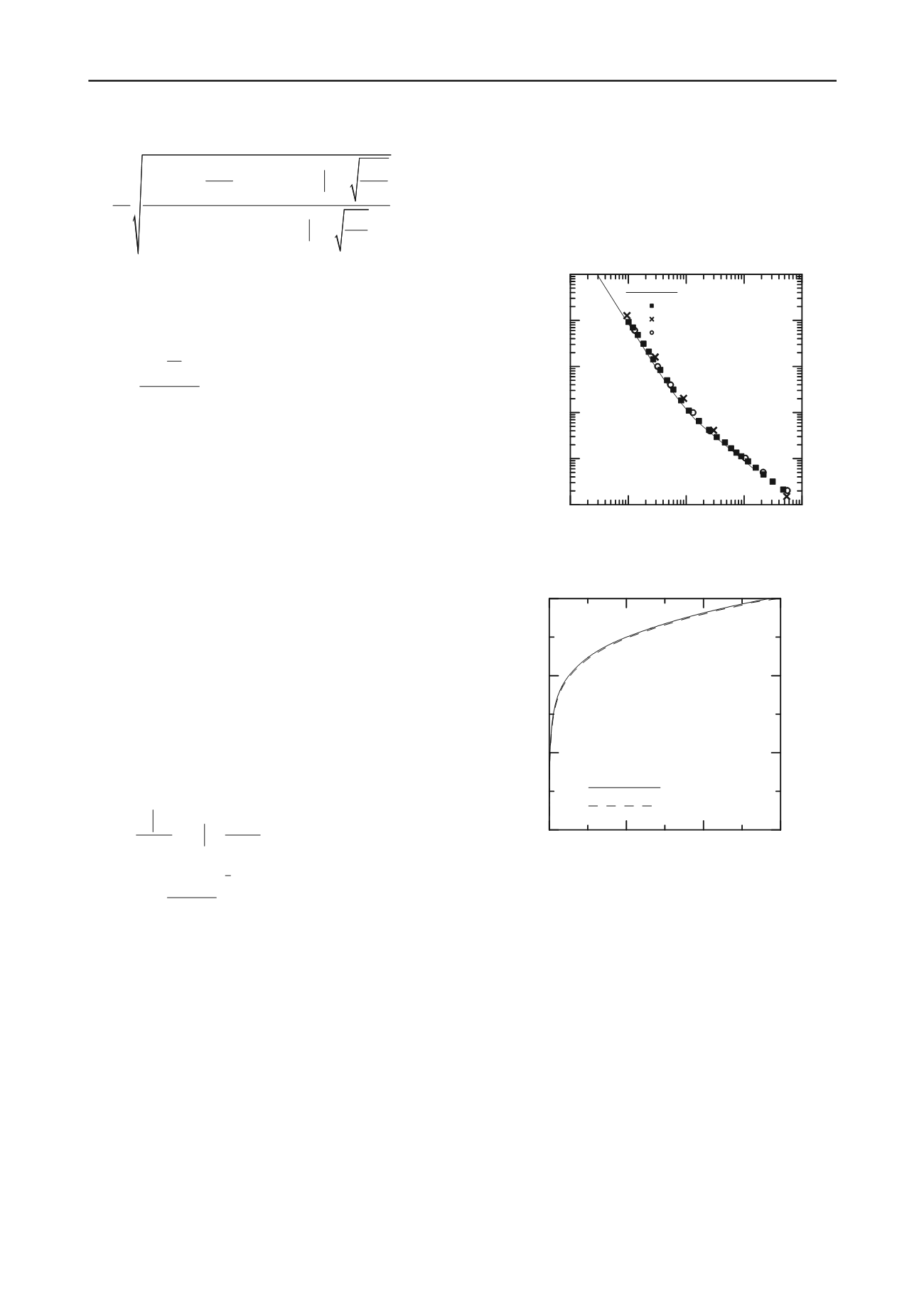
Figure 2 shows the plots of
I
as a function of
t
for piles
embedded in homogeneous soil, as obtained by Guo and
Randolph (1996), Hache and Valsangkar (1978) and Poulos
(1975) and as obtained from the present analysis. It is evident
that the pile responses obtained from the present analysis match
those obtained by others quite well. Figure 3 also shows that,
for a given soil profile (in which
G
s
and
G
p
are constants) and a
given applied torque
T
a
,
I
of
a slender pile is less than that of a
stubby pile. Further, for a given pile geometry,
I
increases as
G
p
/
G
s
increases.
In order to further check the accuracy of the present
analysis, one example problem is solved and compared with the
results of equivalent three-dimensional (3D) finite element
analysis (performed using Abaqus). A four-layer deposit is
considered in which a 30 m long pile with 1.0 m diameter is
embedded. The top three layers are located over 0-5 m, 5-10 m
and 10-20 m below the ground surface. The fourth layer extends
down from 20 m to great depth. The elastic constants for the
four layers are
G
s
1
= 8.6
10
3
kPa,
G
s
2
= 18.52
10
3
kPa,
G
s
3
=
28.8
10
3
kPa and
G
s
4
= 40
10
3
kPa, respectively. This results
in
G
s
1
*
= 4.3
10
3
kPa,
G
s
2
*
= 9.26
10
3
kPa,
G
s
3
*
= 14.4
10
3
kPa and
G
s
4
*
= 20.0
10
3
kPa. The shear modulus of the pile
G
p
= 9.6
10
3
kPa and the applied torque at the head
T
a
= 100
kN-m. Figure 3 shows the angle of twist in the piles as a
function of depth for the two examples described above. It is
evident that the match between the results of the present
analysis and those of the finite element analyses is quite good.
0.01
0.1
1
10
100
Relative Pile-Soil Stiffness,
t
0.01
0.1
1
10
100
1000
Torsional Influence Factor,
I
Present Analysis
Guo & Randolph (1996)
Poulos (1975)
Hache & Valsangkar (1988)
Figure 2.
I
versus
t
for piles in homogeneous soil deposits.
0
0.0002
0.0004
0.0006
Angle of Twist,
p
(radian)
30
20
10
0
Depth,
z
(m)
Present Analysis
3D Finite Element
Pile Diameter = 1.0 m
Pile Length = 30 m
Figure 3. Angle of twist versus depth of a 10 m long pile in a 2-layer
soil deposit.
The effect of soil layering is studied for piles in two-layer
profiles with slenderness ratio
L
p
/
r
p
=
20 and 100 and for
G
p
/
G
s
1
= 1000 (
G
s
1
is the shear modulus of the top layer).
I
is
calculated using the above parameters for different values of
H
1
/
L
p
(
H
1
is the thickness of the top layer) and
G
s
2
/
G
s
1
(
G
s
2
is
the shear modulus of the bottom layer). The values of
I
thus
obtained are normalized with respect to
I
,homogeneous
calculated
for piles in homogeneous soil profiles with
G
s
=
G
s
1
. Figure 4
shows the normalized parameter
I
/
I
,homogeneous
as a function of
H
1
/
L
p
. Note that
H
1
/
L
p
= 0 implies that the pile is embedded in
a homogeneous soil with the shear modulus equal to
G
s
2
.
H
1
/
L
p
= 1 implies that the entire pile shaft lies within the top layer and
the pile base rests on top of the bottom layer. Also note that
I
,homogeneous
corresponds to the case where
H
1
/
L
p
=
. It is
evident from Figure 4 that, for long, slender piles with
L
p
/
r
p
=
100, the presence of the second layer affects pile head response
only if the bottom layer starts within the top 25% of the pile
shaft. For short, stubby piles with
L
p
/
r
p
= 20, the head response
is affected even if the bottom layer starts close to the pile base.


