2676
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
and makes the analysis suitable not only for the design of piled
rafts supporting high rise buildings (generally based on complex
and expensive 3D FEM or FDM analyses) but also for that of
bridges and ordinary buildings.
A description of the BEM formulation adopted in
PGROUPN for the case of pile groups has been presented by
Basile (2003). In a similar fashion, the approach has been
extended to include the raft analysis (including its reciprocal
interaction with the piles) by discretizing the raft-soil interface
into a number of rectangular elements (Fig. 1), whose behaviour
is evaluated using the traditional Mindlin solution. Completely
general loading conditions (axial, lateral and moments) on the
piled raft can be examined, even though only the bearing
contribution of the raft is considered (i.e. the raft-soil interface
is assumed to be smooth). Similarly to the pile analysis, non-
linear soil response is modelled, in an approximate manner, by
adopting a hyperbolic stress-strain model within a stepwise
incremental procedure which ensures that the specified limiting
stresses at the raft-soil interface are not exceeded. Limiting
values of raft-soil contact pressure (based on the traditional
bearing capacity theory) are set for both compression and
tension in order to allow for local bearing failure or lift-off of
the raft from the soil.
The proposed PGROUPN analysis is currently restricted to
the assumption of perfectly rigid raft. In practice, this
assumption makes the analysis strictly applicable to "small"
piled rafts (Viggiani et al. 2012), i.e. those rafts in which the
bearing capacity of the unpiled raft is usually not sufficient to
carry the applied load with a suitable safety margin, and hence
the primary reason for adding piles is to increase the factor of
safety. This generally involves rafts in which the width (
B
r
)
amounts to a few meters (typically
B
r
<15m) and is small in
comparison to the length (
L
) of the piles (
B
r
/L
<1). Within this
range (whose limits should however be regarded as tentative
and indicative only), the raft response may be considered as
truly rigid and hence the design should aim at limiting the
maximum settlement (being the differential settlements
negligible). In practical applications, a simple check on the
validity of the assumption of rigid raft may be performed by
calculating the raft-soil stiffness ratio (
K
rs
) as defined by
Horikoshi and Randolph (1997):
= 5.57
.
(1)
where the subscripts
r
and
s
denote the raft and soil properties,
Figure 1. Load-settlement ratio and piled raft analysed
respectively,
E
is the Young's modulus,
ν
is the Poisson's ratio,
B
r
is the raft breadth,
L
r
is the raft length (with
B
r
≤
L
r
), and
t
r
is
the raft thickness. For values of
K
rs
> 5-10 the raft can be
considered as rigid while a lower limit
K
rs
>
1.5 may be
assumed for practical purposes (Randoph 2003). It is however
observed that the above definition of
K
rs
does not include the
additional stiffening contribution provided by the piles and by
the superstructure which in effect increases the raft rigidity.
Clearly, for "large" flexible rafts (in which
B
r
/L
> 1 according to
the definition by Viggiani), the assumption of rigid raft is no
longer valid and the limitation of differential settlement
becomes one of the design requirements. It is interesting to note
that Poulos (2001) has shown that, except for thin rafts, the
maximum settlement and the load sharing between the raft and
the piles are little affected by the raft rigidity.
3 NUMERICAL RESULTS
3.1
Comparison with Kuwabara (1989)
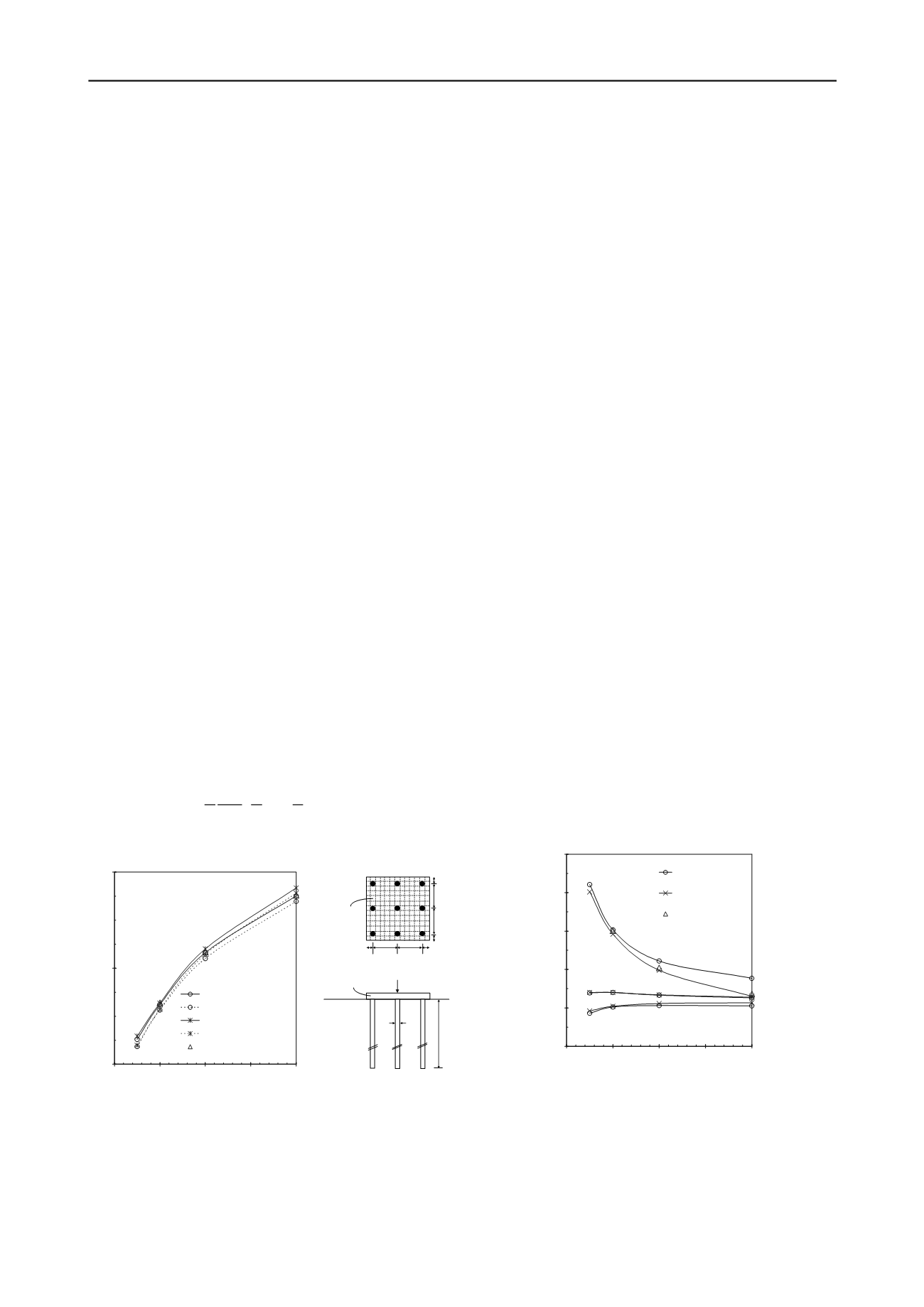
The accuracy of PGROUPN is initially assessed in the linear
elastic range for the piled raft (3x3 group) sketched in Fig. 1.
The figure shows the dimensionless load-settlement ratio
(
P/E
s
Dw
, where
P
is the total applied load and
w
is the
settlement) of the piled raft for a wide range of pile length-
diameter ratios (
L/D
). For comparison, results from the
corresponding free-standing pile group are also reported and
show the small influence of the raft contribution to the resulting
settlement. However, the load distribution is considerably
affected by consideration of the ground-contacting raft, as
illustrated in Figure 2 which shows the percentage of the total
load carried by the raft and by the corner pile as a function of
the
L/D
ratio. For comparison, the load taken by the corner pile
of the pile group is also reported, demonstrating a significant
reduction of corner load in the piled raft as compared to the pile
group. Both figures show a favourable agreement of PGROUPN
with the boundary element solution of Kuwabara (1989) and the
variational approach of Shen et al. (2000).
3.2
Comparison with Poulos (2001)
The effects of soil nonlinearity are examined in the piled raft
(3x3 group) shown in Fig. 3, as reported by Poulos (2001). The
non-linear load-settlement response predicted by PGROUPN
agrees well with the corresponding settlement value obtained by
Poulos using the program GARP (employing a FEM analysis
for the raft and a BEM analysis for the piles), under the
assumption of rigid raft (i.e. a raft thickness
t
r
= 1m giving
K
rs
=
6.1), and for a typical design load
P
= 12 MN (equivalent to an
overall factor of safety of 2.15 against ultimate capacity). For
consistency with the Poulos analysis, an elastic-perfectly plastic
soil model has been adopted in PGROUPN with an assumed
raft bearing capacity of 300 kPa and a pile load capacity of
Figure 2. Load sharing between raft and piles
20
40
60
0
25
50
75
100
L/D
Load-settlement ratio P/(E
s
Dw)
PGROUPN - piled raft
PGROUPN - pile group
Kuwabara (1989) - piled raft
Kuwabara (1989) - pile group
Shen et al. (2000) - piled raft
1.5 5m 5m 1.5m
1.5m
5m
5m
1.5m
L = variable
D=1m
E
p
= 25 GPa
E
s
= 25 MPa
ν
s
= 0.5
Rigid raft
P
PGROUPN
discretization of
raft-soil
interface
0
10
20
30
40
50
0
25
50
75
100
L/D
Load carried by raft/piles (%)
PGROUPN
Kuwabara (1989)
Shen et al. (2000)
Raft
Corner pile (group)
Corner pile (piled raft)


