2362
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
5 tan
exp (1 0.91tan
)
1 0.0025
q
N
(11)
6 CONCLUSION
However, plasticity limit analysis involves certain assumptions:
(1) an associated flow rule, i.e.
=
; (2) rigid plastic strength. The
FEM method can consider the effect of soil stiffness and soil
dilatancy angle on bearing capacity factor and the CSMC model
allows the progressive changes in strength and stiffness during
bearing failure to be captured.
Calculations of the N
q
bearing capacity factor for a circular plate
on weightless sand have been performed using LDFE and the MC
model. The results show that both stiffness and dilatancy angle have
a significant influence on the soil bearing capacity. The bearing
capacity factor N
q
varies by up to 50% for a realistic range of
stiffness. The variation of N
q
induced by the variation of dilatancy
angle is no more than 15%. An empirical relation can be drawn for
the estimation of N
q
, as:
In this paper, the classic Mohr-Coulomb (MC) model is extended to
simulate soil hardening and softening behaviour based on critical
state (CS) soil mechanics. Friction and dilation angles are linked
with soil state parameter in an MC model. This new critical state
Mohr-Coulomb (CSMC) model is verified by single element tests
and large deformation finite element (LDFE) analysis using the
RITSS method. The newly developed CSMC model can be easily
applied to large deformation analysis and shows good stability.
ACKNOWLEDGEMENTS
This research is supported by The National Basic Research Program
of China (973 Program, No. 2012CB026104) and the ARC
Discovery Project DP1096764. The third author is supported by an
ARC Future Fellowship and Shell.
2 tan
(0.6 0.06 ln )
surf
q
E
q
N
e
(12)
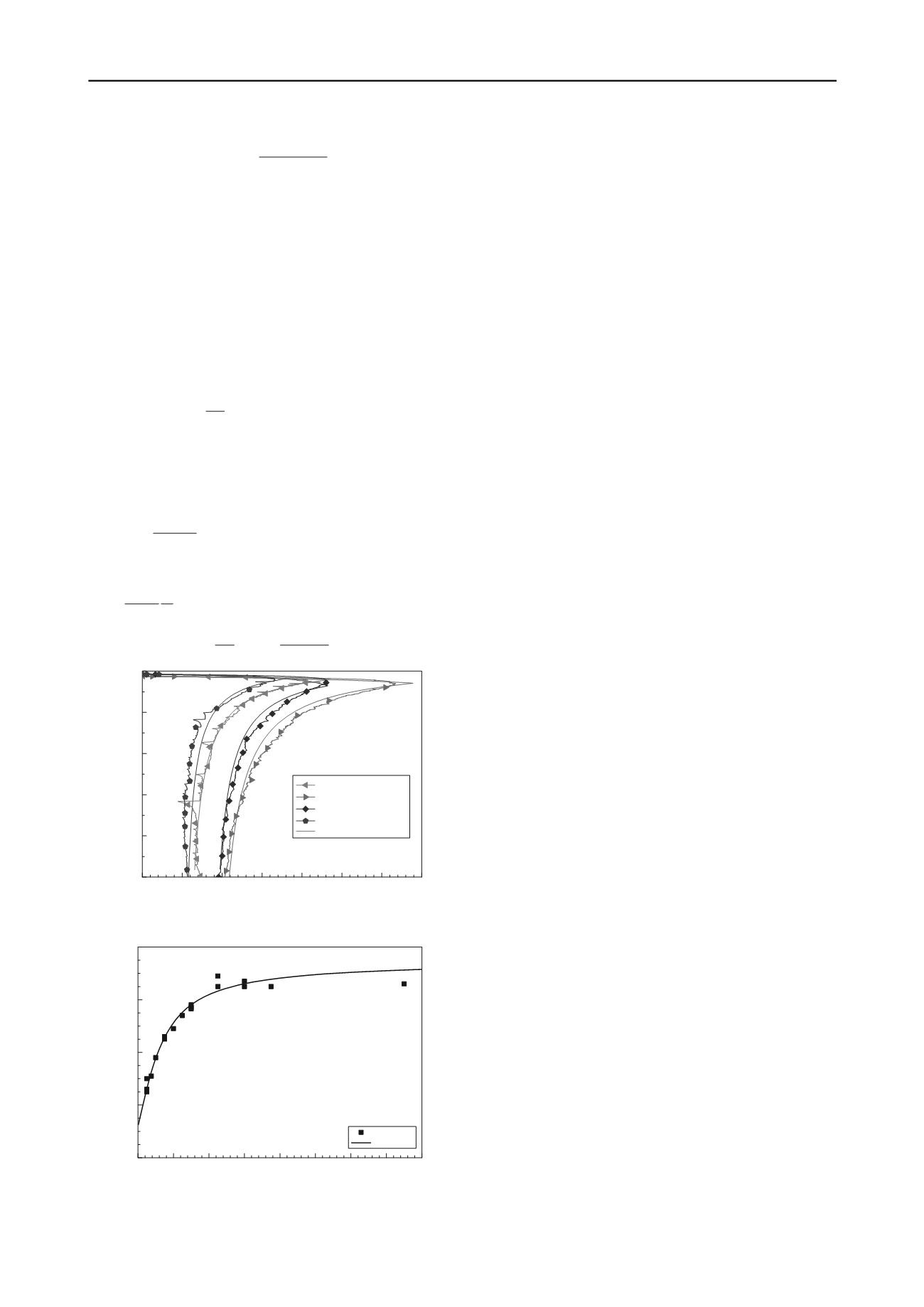
For the plate on weighted sand, the integrated N
q
is found to
vary with soil stiffness, soil weight, soil dilatancy angle and soil
dimension (as shown in Fig. 8). The FEM results (Fig. 9) show that
the integrated N
q
approaches its ultimate value N
q
if
is smaller
than 2, as follows:
REFERENCES
Abbo, A.J. and Sloan, S.W. 1995. A Smooth Hyperbolic Approximation
to the Mohr-Coulomb Yield Criterion. Computers and Structures
54(3): 427-441.
2 tan
0.015
(atan
0.3)(0.65 sin ) exp
q
E
N
D
(13)
Alshibli, K.A. Batiste, S.N. and Sture S. 2003. Strain localization in
sand: plane strain versus triaxial compression. Journal of
Geotechnical and Geoenvironmental Engineering, 129(6): 483-494.
For all the cases, the integrated bearing capacity factor can be
written as (seeing Fig. 8),
Been, K. and Jefferies, M.G. 1985. A state parameter for sands.
Géotechnique, 35(2): 99-112.
tan
0.5
0.45
(0.95 0.009( ) tan
)
1 0.02
qd
surf
qd
q
E d
N
e
D q
E
N N
D
(14)
Been, K., Jefferies, M.G., and Hachey, J. 1991. The critical state of
sands. Geotechnique, 41(3), 365–381.
Bolton, M.D. 1986. The strength and dilatancy of sands. Geotechnique,
36(1): 65-78.
Carter, J.P. and Balaam, N.P. 1995. AFENA users manual:
Geotechnical Research Center, University of Sydney.
Hu, Y.X. and Randolph, M.F. 1998a. H-adaptive FE analysis of elasto-
plastic non-homogeneous soil with large deformation. Computers
and Geotechnics, 23(1-2): 61-83.
0
50
100
150
200
250
300
350
0.5
0.4
0.3
0.2
0.1
0.0
Plate penetration into uniform sand
E=30MPa,
=30.6
o
q
surf
/
D
Coupled bearing capacity factor N
q
=10g/cm
3
,
=2
o
, D=4m
=10g/cm
3
,
=32
o
, D=4m
=2g/cm
3
,
=32
o
, D=40m
=2g/cm
3
,
=2
o
, D=40m
Eq. 14
Hu, Y. & Randolph, M. F. 1998b. A practical numerical approach for
large deformation problems in soil.
Int. J. Numerical and Analytical
Meth. Geomech.
22(5): 327-350.
Li X. Hu, Y.X. and White, D. 2013. Development of a critical state
hyperbolic Mohr-Coulomb model for sand in large deformation FE
analysis. Submitted to Geotechnique.
Li, X.S., Dafalias, Y.F., and Wang, Z.L. 1999. State-dependent
dilatancy in critical-state constitutive modelling of sand. Candian
Geotechnical Journal, 36(4): 599–611.
Ling, H.I. and Yang, S. 2006. A unified sand model based on critical
state and generalized plasticity. J. of Eng. Mech., 132: 1380-1391.
Manzari, M.T., and Dafalias, Y.F. 1997. A critical state two-surface
plasticity model for sands. Géotechnique, 47(2): 255–272.
Martin, C.M. 2004. ABC – Analysis of Bearing Capacity.
.
Fig. 8 Integrated bearing capacity factor N
q
�
0
100 200 300 400 500 600 700 800
0
20
40
60
80
FEM result
Eq. 13
Ultimate coupled bearing capacity factor, N
q
E/
D
Cricular plate penetration into uniform sand
=
=30.6
o
, rough condition
Riemer, M.F. and Seed, R.B. 1997. Factors affecting apparent position
of steady-state line. Journal of Geotechnical and Geoenviormental
engineering, 123(3): 281-287.
Richard F., Wendell, H., Michael, M. and Gioacchino, V. Strain
localization and undrained steady state of sand. Journal of
Geotechnical and Geoenvironmental Engineering, 122(6): 462-473.
Samieh, A.M. and R.C.K. Wong. 1997. Deformation of Athabasca oil
sand in triaxial compression tests at low effective stresses under
varying boundary conditions. Canadian Geotech. J., 34: 985-990.
Taylor, D.W. 1948. Fundamentals of soil mechanics. Wiley. New York.
Verdugo, R., and Ishihara, K. 1996. The steady state of sandy soils.
Soils Foundation, 36(2): 81-91.
Wang, Z.L., Dafalias, Y.F. and Shen, C.K. 1990. Bounding surface
hypoplasticity model for sand. Journal of Engineering Mechanics,
ASCE, 116(5): 983-1001.
Salgado R., Bandini, P. and Karim, A. 2000. Shear strength and
stiffness of slity sand. Journal of Geotechnical and
Geoenvironmental Engineering, 126: 451-461.
Yu, L., Hu, Y.X., Liu, J., Randolph, M. and Kong, X.J. 2012.
Numerical study of spudcan penetration in loose sand overlying
clay. Computers and Geotechnics, 46: 1-12
Fig. 9 Ultimate value of integrated bearing capacity factor N
q
Carraro, H. Prezzi, M. and Salgado, R. 2009. Shear strength and
Stiffness of sands containing Plastic or Nonplastic Fines. Journal of
Geotech. and Geoenviromental Engineering, 135(9): 1167-1178.
g


