2352
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Marine Clay, the standard properties of which have been
reported by Tan (1983). After cyclic loading, the specimens
were immediately subjected to standard consolidated undrained
triaxial monotonic loading to failure. According to Ho et al.
(2012), when undrained cyclic triaxial tests on clays are
conducted at a sufficiently slow rate for pore pressure
equilibration, intrinsic strain rate effects on pore pressure
measurements, effective stress paths and stress-strain
relationships are negligible. Since the focus of this study is not
on strain rate effects, all tests were conducted at relatively slow
rates. Both mid-plane and base pore pressure transducers were
used and pore pressure equilibration is considered to be
achieved when both transducers produce similar excess pore
pressure measurements. All cyclic and post-cyclic triaxial tests
were performed using the GDS Enterprise Level Dynamic
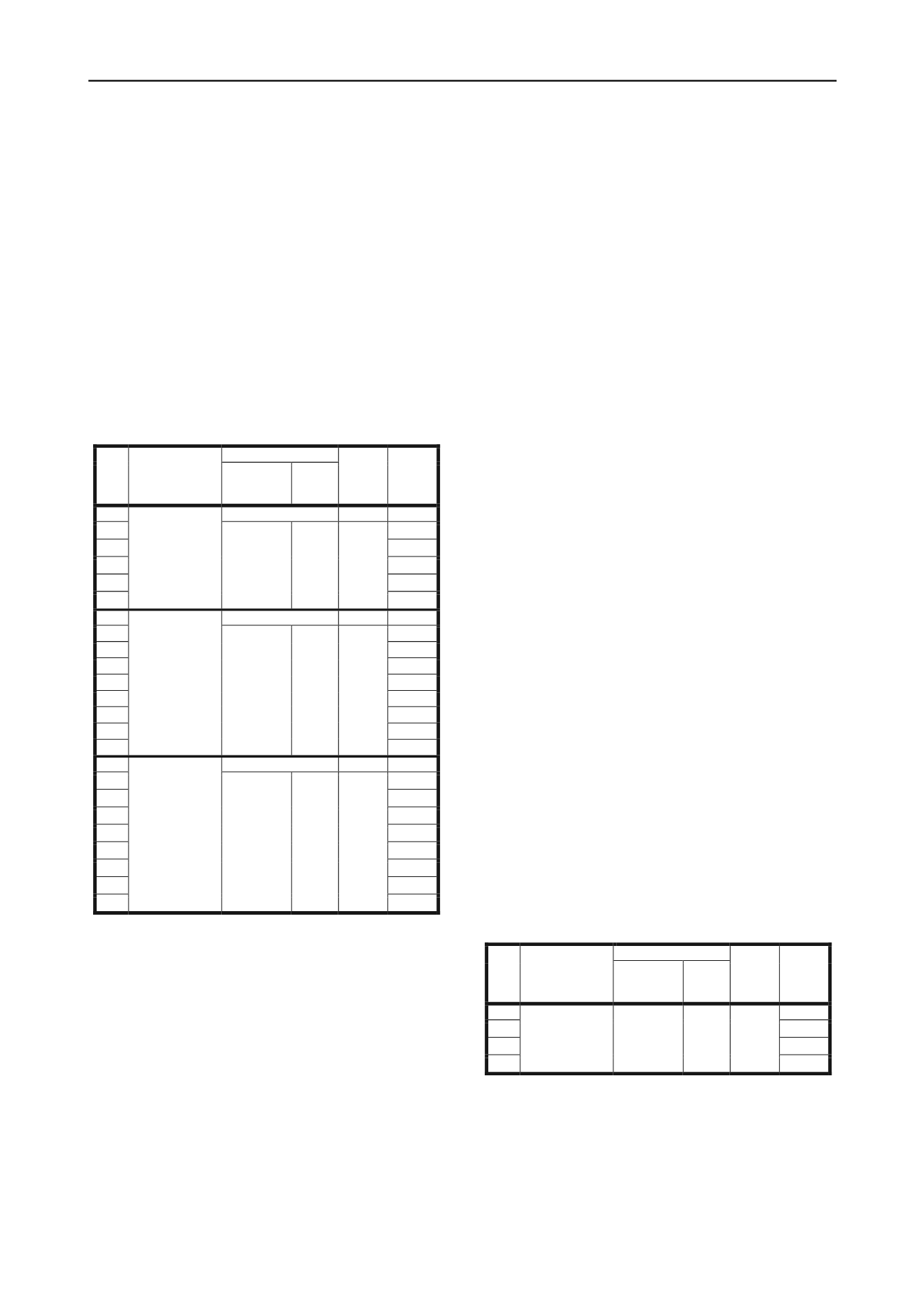
Triaxial Testing System. Table 1 shows the experimental
matrix. Experimental data presented in this study was recorded
at 2-second intervals.
Table 1. Experimental Matrix.
Cyclic Amplitude
No
Effective
Consolidation
Pressure, p
c
’
(kPa)
Amplitude
(mm)
Strain
(%)
Period
(min)
No. of
Cycles
1
-
-
0
2
5
3
10
4
15
5
20
6
50
1
≈
1.4
10
100
7
-
-
0
8
2
9
3
10
4
11
5
12
6
13
20
14
30
15
100
1
≈
1.4
14
100
16
-
-
0
17
2
18
3
19
4
20
5
21
6
22
10
23
30
24
200
1
≈
1.4
60
100
3 EXPERIMENTAL RESULTS AND DISCUSSION
3.1
Cyclic Loading
Normalized stress plots and stress-strain relationships during the
cyclic tests are summarized in Figure 1. The stress path
parameters, i.e. deviator stress (q) and mean effective stress
(p’), are normalized against the effective consolidation pressure
(pc’) for easy comparison between specimens subjected to
different consolidation pressures. Post-cyclic effective stress
paths are included in Figure 1. The critical state line is also
plotted based on data from monotonic triaxial compression tests
where the effective angle of friction for Singapore Upper
Marine Clay is found to be 25.4 degrees. The initial yield locus
and the state boundary surface are assumed to be elliptical.
For Singapore Upper Marine Clay specimens subjected to
the same effective confining pressure, the stress paths and
stress-strain relationships shown on Figure 1 for different
number of applied cycles are similar, reflecting consistency
among the specimens. Due to positive excess pore water
pressure generated during cyclic loading, the mean effective
stress generally decreases during the reloading phase of each
cycle. However, after a certain number of load cycles, the mean
effective stress is observed to increase at the later part of the
loading, just before the maximum deviator stress is reach, as
illustrated in Figure 2. The turning point marking this change in
mean effective stress is hereby termed as “stress reversal” point.
These stress reversal points correspond to a decrease in shear-
induced excess pore water pressure, which would seem to imply
dilative behavior. As the stress reversal points appear after the
normalized mean effective stress decreases beyond a certain
value, post-cyclic monotonic tests are conducted after different
number of load cycles to investigate the factors governing the
onset of this stress reversal behaviour.
3.2
Post-cyclic Loading
Normalized stress plots and stress-strain relationships during the
post-cyclic monotonic tests are summarized in Figure 3, for the
tests listed in Table 1. From Figure 3, the form of the effective
stress paths under post-cyclic monotonic loading depends on the
normalized mean effective stress state of the specimen at the
start of the post-cyclic loading phase. These post-cyclic
effective stress paths may be approximately grouped into three
different regimes, according to the normalized mean effective
stress.
When the normalized mean effective stress state of the clay
specimen at the start of post-cyclic monotonic loading is greater
than 0.6, stress reversal is generally absent and post-cyclic
shearing shows either a decrease or no change in mean effective
stress. This is akin to that of lightly over-consolidated and
normally consolidated clays which tend to increase in density
when sheared.
On the other hand, when the normalized mean effective
stress state of the clay specimen at the start of post-cyclic
monotonic loading falls below 0.5, stress reversal becomes
evident and the effective stress path becomes similar to that of
heavily over-consolidated clays.
Within the range of 0.5 to 0.6, the effective stress path is
approximately vertical indicating that this is a boundary zone
between occurrence or otherwise, of stress reversal.
Unlike the effective stress paths, the normalized stress-strain
relationships are relatively similar. The post-cyclic undrained
strength is almost equal to that without cyclic loading. This
means that the undrained shear strength of Singapore Upper
Marine Clay is not significantly influenced by cyclic loading.
This observation agrees with the findings of Yasuhara et al.
(1992).
3.3
Effect of Cyclic Strain Amplitude
In this section, the results of four additional tests conducted at a
lower strain amplitude are presented; the aim being to
investigate whether strain amplitude has any effect on the stress
reversal. Table 2 summarizes the four additional tests
conducted.
Table 2. Additional Cyclic and Post-cyclic Tests.
Cyclic Amplitude
No
Effective
Consolidation
Pressure, p
c
’
(kPa)
Amplitude
(mm)
Strain
(%)
Period
(min)
No. of
Cycles
1
10
2
15
3
20
4
100
0.5
≈
0.7
14
110
Figure 4 presents the normalized stress plots and stress-strain
relationships obtained from the additional tests. As the applied
cyclic strain amplitude for these four tests has reduced by half
to 0.7%, the number of load cycles required to reach the same
mean effective stress state as previous tests with strain
amplitude of 1.4% has increased proportionally. However, as
Figure 4 shows, the post-cyclic effective stress paths of these
four tests can still be categorized under the three normalized
mean effective stress regimes previously discussed. The
boundaries of these three regimes remain the same despite the


