238
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
the Isotach theory, by which the
a(creep)
value becomes
ultimately zero in a given SL stage (i.e., points C and C’ in
Figure 7). This trend is seen in the test result presented in Figure
8b. In this figure, the reference relation, along with
a(creep)
= 0,
has been drawn based on the value of
UL S
/(
L
at
a(creep)
Δ
=
0) = 1.25 that was obtained from a similar test result as those
presented in Figure 3 and 6. The axial strain increment,
a
Δ
,
between the relations for the
a
a(creep)
values different by a factor of
10 (i.e., one log. cycle of
) is similar until
a(creep)
becomes about 10
-7
%/sec, after which
a
Δ
becomes smaller
towards zero as the relation approaches the reference line.
The largest advantage of the method proposed above is that
creep behaviours at very low strain rates can be observed in a
relatively short. This method becomes reliable when the
reference relation along
a(creep)
= 0 is obtained from such
relations as shown in Figures 3 and 6 by performing many SL
during otherwise UL and RL. Extending the method described
above, creep behaviours at very low strain rates (positive or
negative) starting during otherwise UL/RL can be predicted by
inferring the hysteresis reference relation.
4 CONCLUSIONS
The following conclusions can be derived:
1) The creep strain during normally or over-consolidated
conditions after arbitrary loading history is controlled by the
ratio of the stress at load reversal immediately before to the
stress at sustained loading, irrespective of loading history
and the stress at sustained loading.
2) With Isotach materials, creep behaviour at very low strain
rates as those reached after a long period by sustained
loading starting during otherwise primary loading can be
observed in a relatively short period by performing
sustained loading after a relevant amount of stress reversal.
3) The logarithm of creep strain rate decreases rather linearly
with creep strain until the creep strain rate becomes a
certain low value, followed a drastic decrease toward zero.
5 REFERENCES
Acosta-Martínez H., Tatsuoka, F., and Li, J.-Z. 2005. Viscousproperty
of clay in 1-D compression: evaluation andmodelling.
Proc. 16
th
ICSMGE, Osaka
, 779-783.
Imai, G. 1995. Analytical examination of the foundations toformulate
consolidation phenomena with inherent timedependence.
Keynote
Lecture, Proc. Int. Symp. on Compressionand Consolidation of
Clayey Soils, IS Hiroshima
. (2) 891-935. Rotterdam: Balkema.
Kawabe, S., Kaihara, K. and Tatsuoka, F. 2009. Non-Isotach viscous
property and its simulation in drained one-dimensional compression
on clay.
Proc. of 44
th
Conf. on Geotechnical Eng., Japan
Geotechnical Society
,
Yokohama
, 237-238. (in Japanese)
Kawabe, S., Kongkitkul, W. & Tatsuoka, F. 2011. 1D Compression
with Unload/Reload Cycles on Soft Clay and its Simulation.
Proc.
14
th
Asian Regional Conference on SMGE, Hong-Kong, CD
.
Kongkitkul, W., Kawabe, S., Tatsuoka, F. and Hirakawa, D. 2011. A
simple pmeumatic loading system controlling stress and strain rates
for one-dimensional compression of clay.
Soils and Foundations
51
(1), 11-30.
Leroueil, S., and Marques, M.E.S. 1996. Importance ofstrain rate and
temperature effects in geotechnical engineering.
S-O-A Report,
Measuring and Modeling TimeDependent Soil Behavior, ASCE
Geotech. Special Publication
. 61, 1-60.
Leroueil, S., Perret, D., and Locat J. 1996. Strain rate andstructuring
effects on the compressibility of a youngclay.
Measuring and
Modeling Time Dependent Soil Behavior,ASCE Geotech. Special
Publication
61, 137-150.
Leroueil, S. 2006. Suklje’s Memorial Lecture – The isotache approach:
Where are we fifty years after its development by Professor Suklje?.
Proc. European-Danube Conference on Geotechnical Engineering,
Ljubljana,
1, 55-88.
Niemunis, A., and Krieg, S. 1996. Viscous behaviour ofsoil under
oedometric conditions.
Canadian GeotechnicalJournal
33, 159-168.
Tanaka, H. 2005. Consolidation behaviour of natural soils around
p
c
value - long term consolidation test -.
Soils and Foundations
, 45(3)
83-95.
Tatsuoka,F., Masuda,T. and Siddiquee,M.S.A. 2003. Modelling the
stress-strain behaviour of sand in cyclic plane strain loading.
Geotechnical and Environmental Engineering, Journal of
Geotechnical and Environmental Engineering, ASCE
, 129 (6) 450-
467.
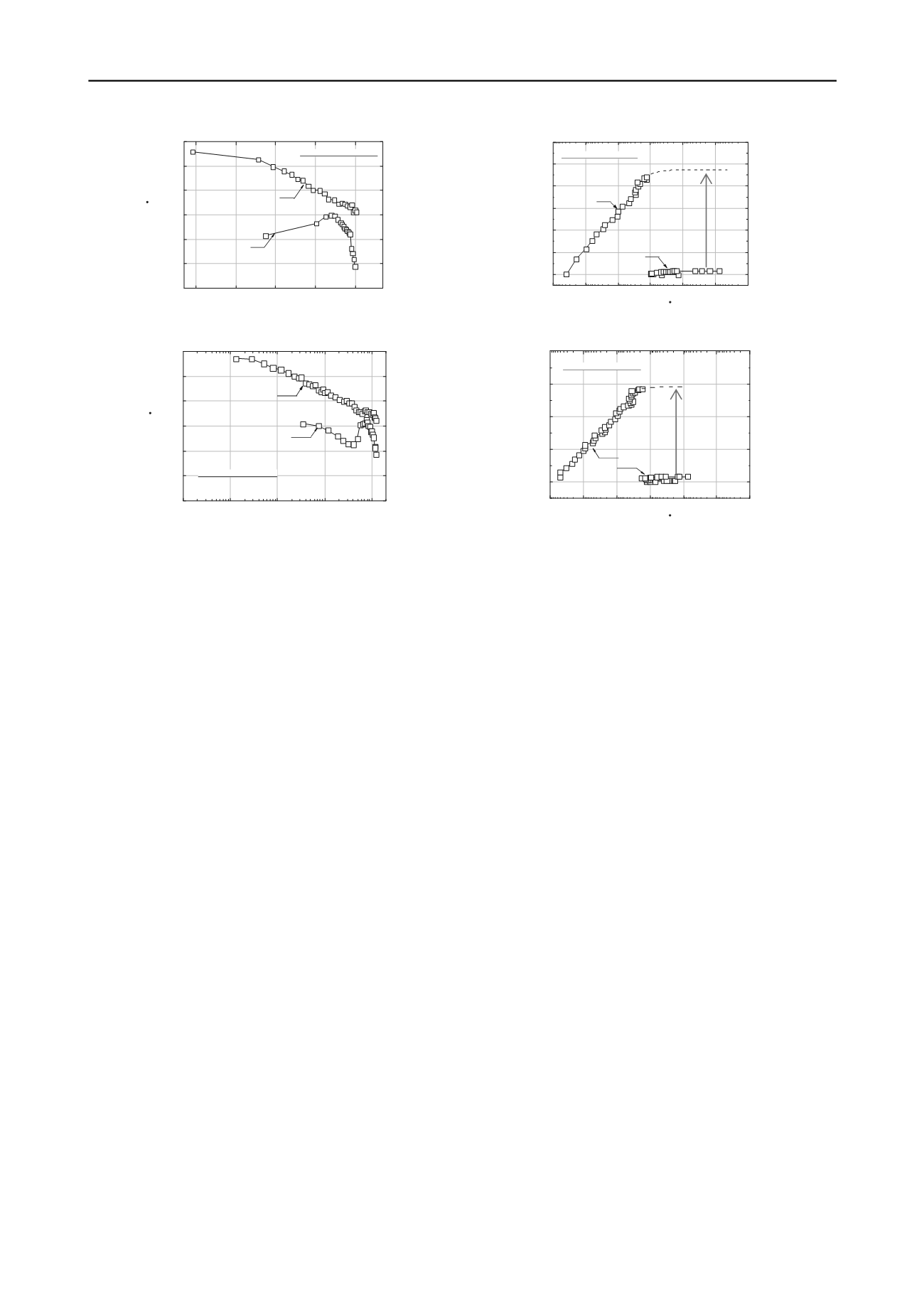
Figure 9. Test KLN1101 (SL1 and SL2): a)
Δt
log
log
a(creep)
relations; and b)
a(creep)
a(creep)
log
Δ
relations
100
1000
10000 100000 1000000
1E-10
1E-9
1E-8
1E-7
1E-6
1E-5
1E-4
TestName:KLN1101
Creep axial strain rate,
a(creep)
(%/sec)
Elapsed time,
t (se
SL1
c)
SL2
1E-4 1E-5 1E-6 1E-7 1E-8 1E-9 1E-10
0.0
0.2
0.4
0.6
0.8
1.0
1.2
Creep axial strain,
a(creep)
(%)
Creep axial strain rate,
TestName:KLN1101
a(creep)
(%/sec)
SL1
SL2
b)
a)
Figure 10. Test FJM1104 (SL1 and SL2): a)
log
Δt
log
a(creep)
relations; and b)
a(creep)
a(creep)
log
Δ
relations
a)
b)
100
1000
10000 100000 1000000
1E-10
1E-9
1E-8
1E-7
1E-6
1E-5
1E-4
SL02
Creep axial strain rate,
a(creep)
(%/sec)
Elapsed time,
t (sec
SL01
)
Test Name: FJM1104
1E-4 1E-5 1E-6 1E-7 1E-8 1E-9 1E-10
0.0
0.5
1.0
1.5
2.0
Test Name:FJM1104
SL02
Creep axial strain,
a(creep)
(%)
Creep axial strain rate,
a(creep)
(%/sec)
SL01


