229
Technical Committee 101 - Session I /
Comité technique 101 - Session I
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
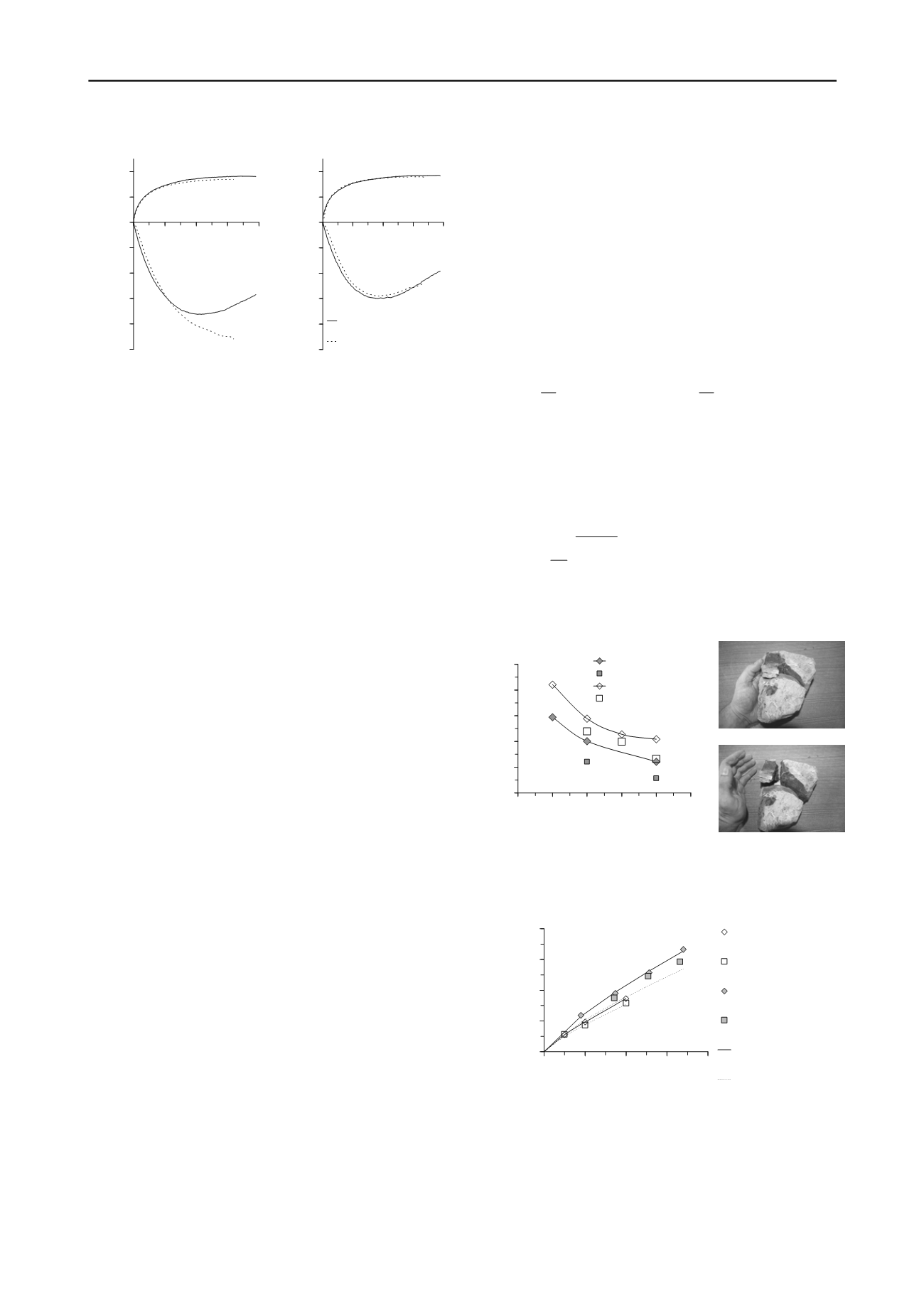
-5
-4
-3
-2
-1
0
1
2
0 5 10 15 20
Axial strain %
Volumetric strain (%)
q/p'
3
=400 kPa
-5
-4
-3
-2
-1
0
1
2
0 5 10 15 20
Axial strain %
Volumetric strain (%)
STV1-dmax=40mm
STV2-dmax=160mm
q/p'
3
=300 kPa
(b)
Figure 4. Courbes de contrainte-déformation pour (a) CP and (b) STV
La grande cellule triaxiale (1 000mm) a été conçue pour
supporter des charges verticales jusqu'à 2 000 kN. Le système
est composé d'une base en acier rigide fixée sur une dalle en
béton précontrainte. La cellule peut supporter une pression de
confinement de 1,5 MPa. L’enveloppe cylindrique de la cellule
est constituée d’une double paroi. Un système de contrôle-
commande en continu maintient la même pression dans les deux
chambres, en permettant les échanges à l’aide d’une servovalve
automatique. Par conséquent, le cylindre intérieur reste
indéformable pendant l’essai et la variation de volume d’eau
dans le compartiment intérieur est uniquement due à la
déformation volumique de l'échantillon et à la pénétration du
piston. Une description exhaustive des appareils triaxiaux se
trouve dans Hu et al. (2011).
Les échantillons sont préparés par couches successives,
compactées par vibrations à l’aide d’une aiguille vibrante. Les
indices des vides initiaux sont de 0,854 ± 0,03 pour CP et de
0,493 ± 0,03 pour STV. La Figure 4 montre la réponse
mécanique lors des essais de cisaillement drainés à une
contrainte effective de confinement
'
3
entre 200 et 400 kPa. La
Figure 3 montre les granulométries associées avant et après les
essais à
'
3
=400 kPa. Sur les Figures 3 et 5, on voit qu'il existe
un effet d’échelle sur la résistance mécanique des deux
enrochements, avec un taux de rupture des grains plus élevé
(Figure 3) et un angle de frottement au pic inférieur (Figure 5)
pour les matériaux plus grossiers. Ceci est cohérent avec l'effet
d’échelle sur la résistance à l'écrasement des particules (voir
Figure 2). Néanmoins, nous n'avons pas observé un effet
d’échelle significatif dans la réponse volumique (Figure 4).
Marachi et al. (1969) montrent des résultats similaires lorsqu'ils
comparent des enrochements de granulométries homothétiques.
Une explication possible de cette évolution particulière de la
déformation volumique pourrait être le rapport relativement
élevé entre
d
max
et le diamètre de l’échantillon (environ 1/6). De
même, les essais sont conduits jusqu’à une déformation axiale
de 20% : les particules grossières pourraient ne pas se déplacer
suffisamment pour se démêler après la rupture et ainsi permettre
plus de contractance. En fait, comme le montre la Figure 6, nous
avons observé, après essai, plusieurs grosses particules cassées
qui semblent être intactes sans déplacement des fragments
brisés.
4 METHODE PREDICTIVE
En considérant que les ruptures individuelles de granulats
affectent la résistance au cisaillement de l’ensemble du milieu
granulaire, Frossard (2009) (voir aussi Frossard et al., 2012) a
proposé une méthode rationnelle afin de prédire les effets
d’échelle sur les enveloppes de résistance au cisaillement des
enrochements. Il a considéré deux granulométries
homothétiques (
G
1
la plus fine et
G
2
la plus grossière) sous le
même type de chargement, avec la même compacité, la même
minéralogie et la même forme initiale des grains, et cherché
quelles conditions assuraient un même taux de ruptures dans les
deux milieux granulaires sous contraintes. Pour cela, une même
probabilité de survie doit être assurée pour deux granulats
homologues de
G
1
et
G
2
, et l’on dispose de la relation suivante
pour la résistance à l’écrasement:
G2
=
G1
(d
2
/d
1
)
-nd/m
(d’après
l’Eq.1) où
G1
et
G2
sont les résistances à l'écrasement des
granulats de
G
1
et
G
2
, respectivement.
Frossard (2009) a ensuite montré que pour obtenir le même
taux de rupture dans les matériaux granulaires sous cisaillement,
la relation précédente doit être vérifiée par les états de
contrainte {
,
n
} des enveloppes de cisaillement des deux
assemblages granulaires homologues:
/
/
2
2
2
1
2
1
1
1
d
d
n m
n m
G G
n G n G
d
d
et
d
d
(2)
En faisant l’hypothèse, pour le matériau
G
1
avec des
paramètres calés
A
G1
et
b
G1
, d’une enveloppe de rupture telle
que celle proposée par De Mello (1977) [
=A.
n
b
], une
enveloppe de rupture peut être prédite pour
G
2
en utilisant
l'Eq.2 :
1
1
2
1
1
2
1
2
G
G d
b
Gn
m
b n
G G
d
d
A
(3)
On remarque que dans l'Eq.2 , l’effet d’échelle affecte le
coefficient
A
, mais pas l’exposant
b
.
36
40
44
48
52
56
0 100 200 300 400 500
Confining pressure (kPa)
Peak friction angle (°)
CP1: dmax=40mm
CP2: dmax=160mm
STV1: dmax40mm
STV2: dmax160mm
Figure 5. Angles de frottement au pic
Figure 6. Gros
granulats de STV
récupérés après essai
triaxial.
0.0
0.2
0.4
0.6
0.8
0.0 0.2 0.4 0.6 0.8
Normal stress (MPa)
Shear stress (MPa)
CP1
CP2
STV1: dmax=40mm
STV2: dmax=160mm
De Mello's fitting
Prediction for CP2 &
STV2
Figure 7. Effet d’échelle sur la résistance au cisaillement
La Figure 7 montre la comparaison entre mesures et prédictions
pour les enveloppes de cisaillement pour les deux matériaux CP
et STV : en partant du meilleur calage de l’expression de De
Mello sur les mesure réalisées sur CP1 et STV1 (
d
max
=40mm),
on a réalisé la prédiction issue de l'Eq. 2 pour CP2 et STV2


