2622
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
element, j, is
j
. The displacement at the centre of an element, i,
due to stresses acting on element, j, are obtained by the method
described by Poulos and Davis (1980).
Integrating numerically, the Mindlin’s equation for a point
load in the interior of a semi-infinite elastic continuum over the
cylindrical periphery of the element, the displacement,
s,ij
, of
the soil adjacent to the centre of the i
th
element due to stress,
j
,
acting on the element, j, considering deformation
modulus, E
s
,
of the soil, increases linearly with the depth as
L
z
E zE
s
so
s
1 )(
is obtained as
j
i
s
ijS
so
ijS
L
z
I
E
d
.
.
1
.
,
,
(1)
where I
s,ij
– is the soil displacement influence coefficient.
The total soil displacement,
s,i
, adjacent to node ‘i’ due to
stresses on all the elements of the GPA, is obtained by summing
up all the displacements at node ‘i’, as
n
j
j
i
s
ijS
s
iS
L
z
I
E
d
1
,
0
,
.
1
(2)
The vertical soil displacements adjacent to all the nodes are
collected to arrive at
'
S
so
S
I
E
d
(3)
where {
s
} and {
} are respectively the soil displacement
and stress vectors of size, n, and elements of the matrix
'
S
I
are
'
,
'
,
.
1
i
z
I
I
s
ij S
ij S
- non-dimensional soil displacement
influence coefficient of GPA, where Z’
i
=Z
i
/L- normalized depth
at i
th
element.
s
=0
0.25
0.5
1
2
0
0.5
1
0
1
2
3
z/L
E
s
/E
so
Fig. 3 Variation of E
s
with Depth – Effect of
s
gp
=0
0.25
0.5
1
2
0
0.5
1
0
1
2
3
z/L
E
gp
/E
gpo
Fig. 4 Variation of E
gp
with Depth – Effect of
gp
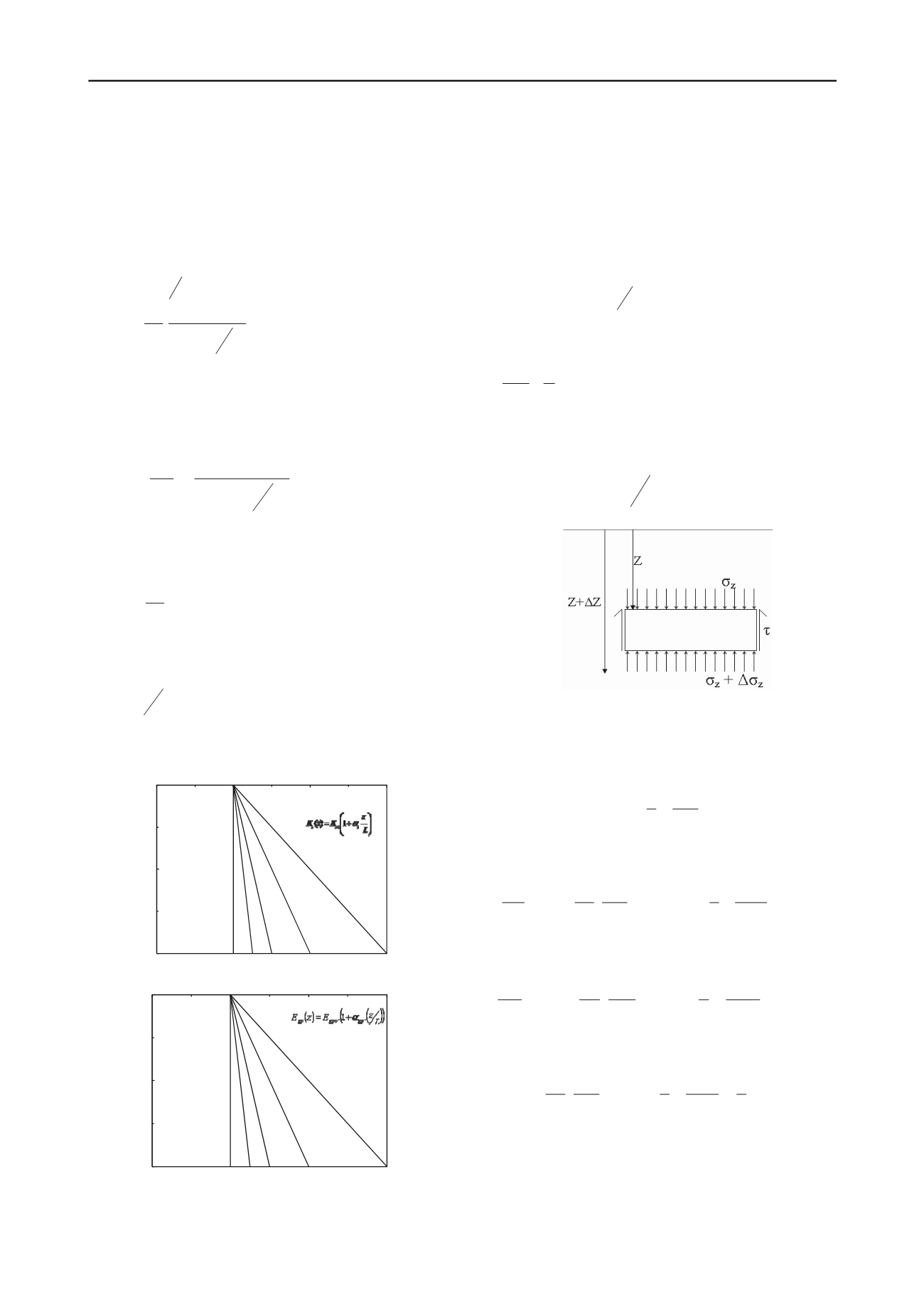
2.1 DISPLACEMNTS OF GPA
The vertical displacements of GPA are obtained considering
it to be compressible. Figure 5 depicts the stresses on an
infinitesimal element of GPA of thickness,
z. Poulos and
Davis (1980) have established that lateral/radial stresses have
negligible effect on the vertical displacements. Considering the
deformation modulus of the granular material, E
gp
, to increase
linearly with depth, z, as
L
z
E zE
gp
gpo
gp
.
1.
(4)
The equilibrium of forces in the vertical direction reduces to
0 4
d dz
d
z
(5)
where
z
is the normal stress in to the GPA. The stress-
strain relationship for GPA material, is
dz
dE E
gp
gp
z gp
z
.
.
(6)
Fig. 5 Stresses acting on an Infinitesimal Element
where
z
and
gp
are respectively the axial strain and GPA
displacement. Substituting for modified E
gp
the stress-strain
Equation 6 is modified as
dz
d
L
z
E
E
gp
gp
gpo
z gp
z
.
.
1
.
(7)
Differentiating Equation 7 with respect to depth, z,
dz
d
L
z
E
dz
d
L
E
dz
d
gp
gp
gpo
gp
gp
gpo
z
2
.
.
1.
.
(8)
On simplification the differential Equation 8 becomes
.
.
.
1
2
dz
d
L
z
dz
d
L
E
dz
d
gp
gp
gp
gp
gpo
z
(9)
Combining Equations 5 and 9 simplify
0 4
.
.
1
2
d
dz
d
L
z
dz
d
L
E
gp
gp
gp
gp
gpo
(10)
Equation 10 is solved along with the boundary conditions: at
z =0 (i.e. at the top of GPA) P=0 (Free boundary) and at z=L
(tip of the GPA), P=P
0
(the applied load). Equation 10 written in
finite difference form reduces to


