Actes du colloque

2620

Proceedings of the 18

th

International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013

on the large particles have also been found by Cheng and Minh

(2009) to be effective in granular mixtures.

The peak shear stress values obtained during the shearing of the

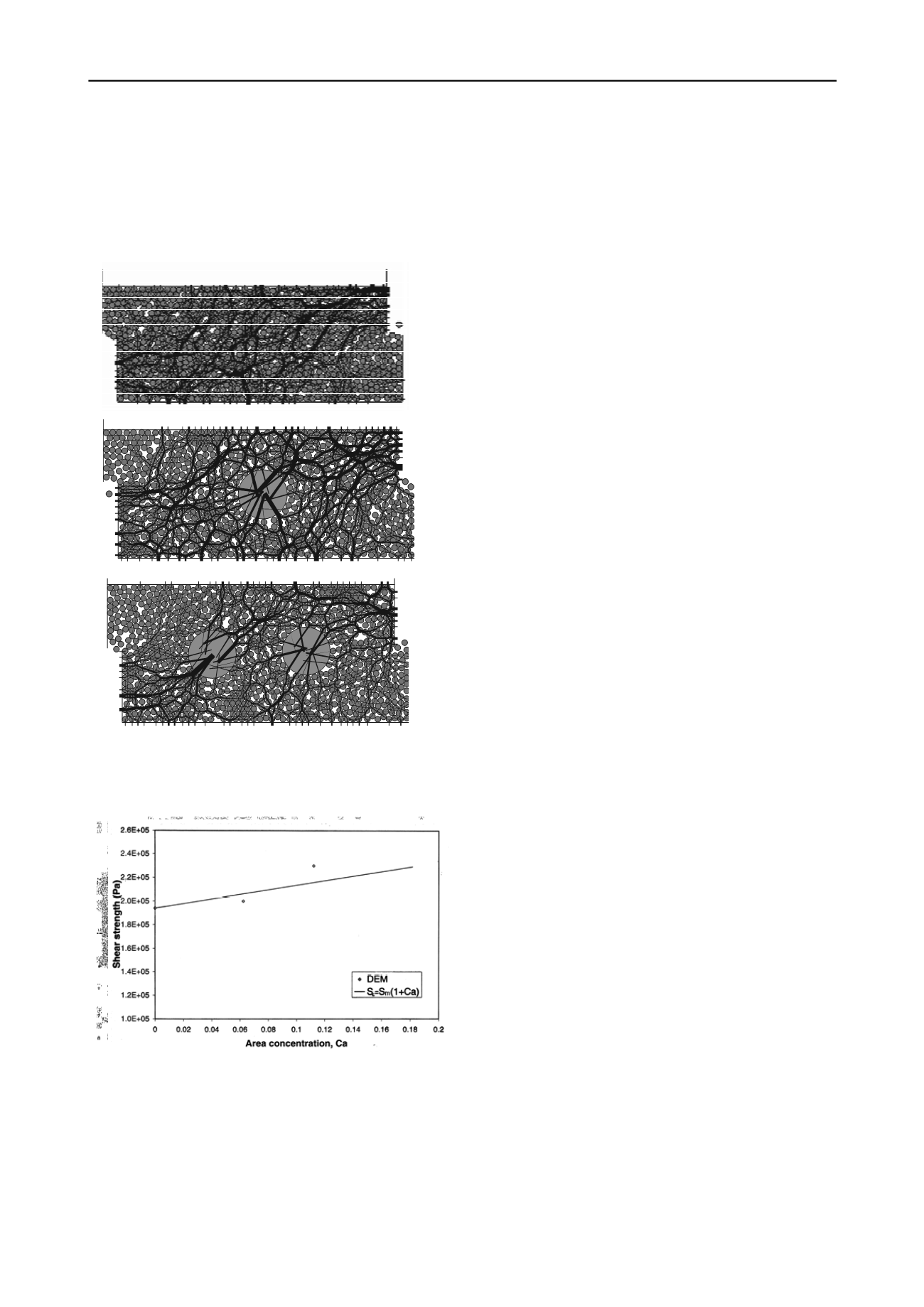
mixtures shown in Figs. 6 and 7 were plotted against the area

concentration of the large cylinders in the mixture. The result of

the plot is shown in Fig. 8.

Figure 7. Force chains in the samples with zero, one and two large

particles at a horizontal shear displacement equal to 3.5 mm.

Figure 8. Shear strength versus the area concentration of the large

cylinders in the simulated granular mixture.

An analysis of Fig. 8 indicates that the presence of the large

cylinders in the mixture has a reinforcing effect. That is, as the

number of large cylinders increase in the mixture, its shear

strength also increases. The best fit line shown in Fig. 8 has an

equation of the form:

S

c

= S

m

(1 + C

a

)

(2)

which is very similar to Eq. (1).

It should be noted that the DEM simulations did not represent

exactly the shape of the particles forming part of the laboratory

experiments. Also, the sizes of the particles used in the

laboratory experiments were different than those used in the

DEM simulations. However, the general results of the

laboratory tests are corroborated by the DEM simulations. In

addition, the DEM simulations help to explain the way internal

forces are transmitted through the particles in the laboratory

experiments. Thus, for the case of real sand-gravel mixtures, it

is expected that the shear strength of these mixtures will

increase with the volume concentration of the gravel in the

mixtures. Also, it should be noted that for the case of

embankments and natural slopes, the effectiveness of the

oversized particles on the shear strength of the mixtures forming

these structures will depend upon if the large particles are

located on or near the critical failure surface (Fig.1).

4 CONCLUSIONS

In the present study the shear strength of simulated granular

mixtures made of granular matrix in which large particles are

embedded was carried out using laboratory and numerical

analyses. Results from using both approaches indicated that the

presence of the large particles has a reinforced effect in the

mixtures. That is, the greater thenumber of the large particles in

the mixture, the greater is the shear strength of the mixtures.

5 ACKNOWLEDGEMENTS

The work described herein was supported by Grants No. CMS:

0124714 and CMS: 0301815 to the University of Pittsburgh

from the National Science Foundation, Washington, D.C. This

support is gratefully acknowledged

6 REFERENCES

Budiman, J.S., Mohamadi, J., and Bandi, S. (1995). Effect of large

inclusions on liquefaction of sands. In: Static and Dynamic

Properties of gravelly Soils, Evans, M.D., and Fragaszy, R.J. (eds),

ASCE’s Geotechnical Special Publication No. 56

: 48-63.

Cheng, Y.P. Minh, N.H. (2009).DEM investigation of particle size

distribution effect on direct shear behavior of granular

agglomerates.

Powders and Grains 2009

, M. Nakagawa

(Editor), American Institute of Physics, New York, 401-404.

Fragaszy, R.J., Su, J., Sidiqqi, F.H., and Ho, C.L. (1992).Modeling

strength of sandy gravel.

Journal of Geotechnical Engineering

,

ASCE, 118(6):920-935.

Itasca Consulting Group, Inc. (2002).

PFC2D(Particle Flow Code in

Two Dimensions) version 3.0

. Minneapolis.

Magier, J. and Ravina, I. (1982).Rock fragments and soil depth as

factors in land evaluation of Terra Rossa.

Soil Science Society of

America (SSSA) Special Publication No. 13

: 13-30.

Poesen, J., and Lavee, H. (1994).Rock fragments on top soil:

significance and processes

. Catena

, 23(1-2): 1-28.

Vallejo, L.E. (1989). An extension of the particulate model of stability

analysis for mudflows.

Soils and Foundations,

29 (3):1-13.

Vallejo, L.E. (1991). A plane stress direct shear apparatus for testing

clays.ASCE

Geotechnical Special Publication No

.27 (II

)

: 851-

862.

Vallejo, L.E. (2001). “Interpretation of the limits in shear strength in

binary granular mixtures.”

Canadian Geotechnical Journal

,

38:1097-1104.

concentration of the large cylinders in the mixture. The result of

the plot is shown in Fig. 8.

Figure 7. Force chains in the samples with zero, one and two large

particles at a horizontal shear displacement equal to 3.5 m.

Figure 8. Shear strength versus the area concentration of the large

cylinders in the simulated granular mixture.

An analysis of Fig. 8 indicates that the presence of the large

cylinders in the mixture has a reinforcing effect. That is, as the

number of large cylinders increase in the mixture, its shear

strength also increases. The best fit line shown in Fig. 8 has an

equation of the form:

S

c

= S

m

(1 + C

a

) (2)

which is very similar to Eq. (1).

It should be noted that the DEM simulations did not represent

exactly the shape of the particles forming part of the laboratory

experiments. Also, the sizes of the particles used in the

laboratory experiments w re diff rent than those used in the

DEM simulations. How ver, the g neral results of the

laboratory tests are corr borated by the DEM simulations. In

addition, the DEM simulations help to explain the way internal

forces are transmitted through the particles in the laboratory

experiments. Thus, for the case of real sand-gravel mixtures, it

is expected tha the shear strength of th se mixtures will

increase with the volume concentration of the gravel in the

mixtures. Also, it should be noted that for the case of

embankments and natural slopes, the effectiv ness of the

oversized particles on the shear strength of the mixtures forming

th se structures will d pend upon if the large particles are

located on or near the critical failure surface (Fig.1).

4 CONCLUSIONS

In the pr sent study the shear strength of simulated granular

mixtures made of granular matrix in which large particles are

embed ed was carried out using laboratory and numerical

naly es. Results from using both approaches indicated that the

pr sence of the large particles has a reinforced effect in the

mixtures. That is, the greater thenumber of the large particles in

the mixture, the greater is the shear strength of the mixtures.

5 ACKNOWLEDGEMENTS

The work described h rein wa supported by Grants No. CMS:

0124714 and CMS: 30 815 to the University of Pittsburgh

from the National Science Foundation, Washington, D C. This

support is gratefully acknowledged

6 REFERENCES

Budiman, J.S., Mohamadi, J., and Bandi, S. (1995). Effect of large

inclusions on liquefaction of sands. In: Static and Dynamic

Properties of gravelly Soils, Evans, M D., and Fr gaszy, R.J. (eds),

ASCE’s Geotechnical Special Publication No. 56

: 48-63.

Cheng, Y.P. Minh, N.H. (2009).DEM investigation of particle size

distribution ffect on direct shear behavi r of granular

agglomerates.

Powders and Grains 2009

, M. N k g wa

(Editor), America Institute of Phy ics, New York, 401- 04.

Fr gaszy, R.J., Su, J., Sidiqqi, F H., and Ho, C.L. (1992).Modeling