2046
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
roughly 4
o
to 5
o
larger than the values corresponding to triaxial
compression conditions
c,TX
(=31.6
o
and 30.2
o
, respectively).
(cr)
R
eq
c,TX
9
2 (4)
100%
o
D
15
30
45
60
75
90
D
R
(%)
0.50
0.75
1.00
1.25
1.50
mob
/
c
Toyoura sand
Ottawa sand
For the calculation of both
K
A,min
and
K
A,cr
using Eq. (1), the
wall-soil interface friction angle
can be conservatively set
equal to
c
estimated as arctan[sin(
c,TX
+4
o
)]. Finally, it should
be pointed out that, according to the numerical results, the point
of application of the active earth thrust at MPS is at a distance
roughly
H
/3 from the wall base, while for the residual state is
slightly smaller (roughly 0.3
H
).
4
CONCLUSIONS
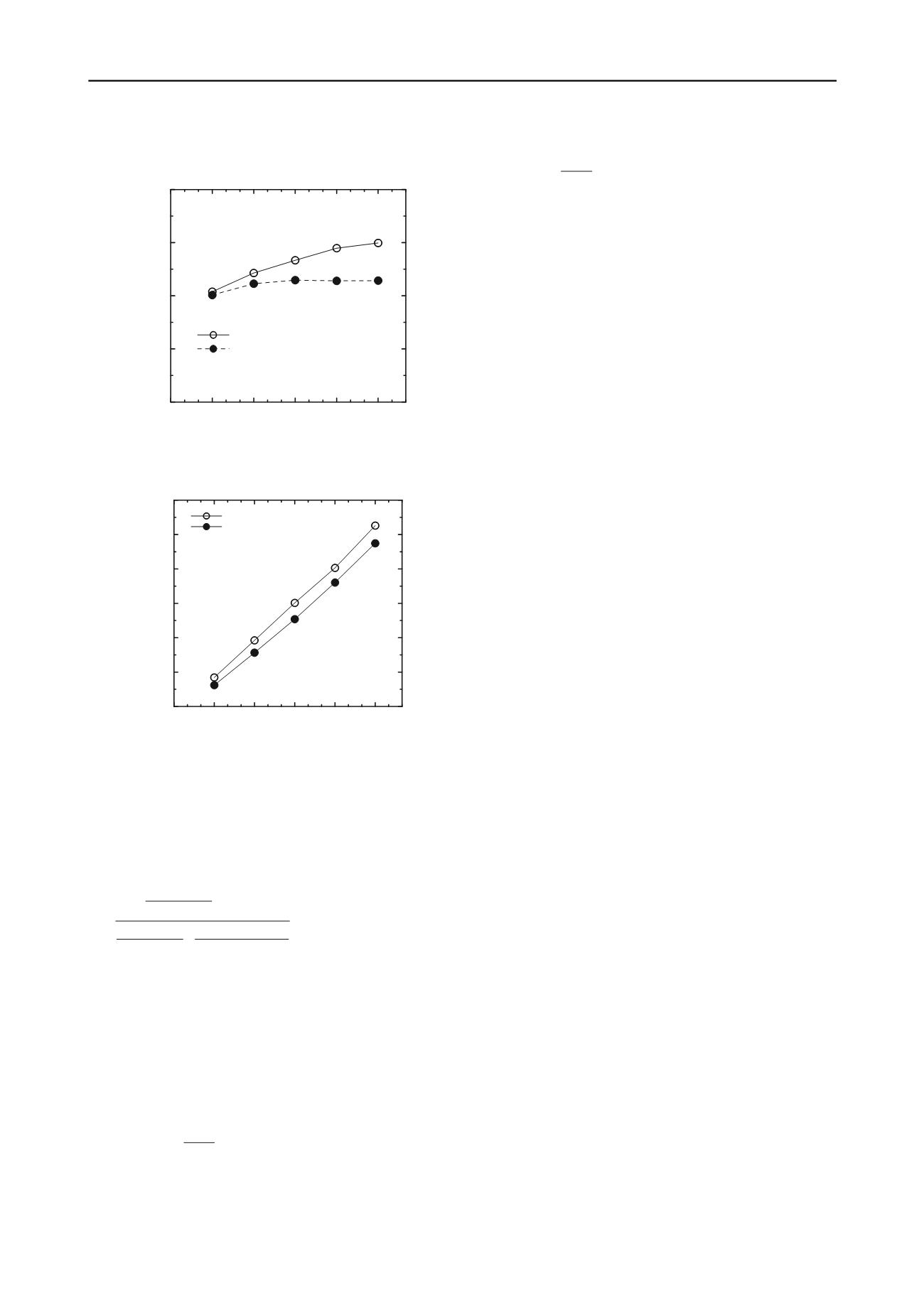
Figure 6. Ratio of the
mobilized along the wall-soil interface at MPS
to the
corresponding to critical state conditions.
This paper presented the results of a set of finite element
analyses of a retaining wall supporting sand. Based on
numerical results, the active earth pressure coefficient attains a
minimum value
K
A,min
at wall crest displacements of the order of
0.005
H
. Hence, from a practical standpoint, this state is of
limited relevance to ultimate limit state (ULS) design; it is
possibly representative of a serviceability limit state (SLS)
design. A residual (maximum) value
K
A,cr
associated to full
mobilization of critical state inside the soil mass is practically
reached at crest displacements of the order of 0.1
H
.
15
30
45
60
75
90
D
R
(%)
0.0
5.0
10.0
15.0
20.0
25.0
30.0
eq
-
c,TX
(
o
)
Toyoura sand
Ottawa sand
minimum active pressure state
(a)
The
K
A
to be used in ULS calculations can be estimated
using the proposed Eq. (2), provided that the designer knows
a
priori
the wall crest displacement
u
C
corresponding to ULS. In
case there is a structure founded on the supported soil, the
u
C
can be set equal to the allowable foundation displacement value
compatible with the ULS for the structure, established
according to design code provisions. In the opposite case, the
u
C
could be set equal to 7 times the horizontal base displacmenet
required for wall foundation failure. In the case of granular
foundation soils, this base displacement can be conservatively
taken as 0.05 times the base width.
Figure 7. Equivalent value of the friction angle to be used in the
calculation of
K
A,min
.
5
REFERENCES
Abbo, A.J. and Sloan, S.W. 2000.
SNAC, User manual, Version 2.0
.
Deptartment of Civil, Surveying and Environmental Engineering,
University of Newcastle, Callaghan, Australia.
3.4
Expression for the estimation of K
A
The variation of the earth pressure coefficient
K
with crest
displacement
u
C
observed in Figs. 4 and 5 can be described
mathematically by the following equation:
Dafalias, Y.F., Papadimitriou, A. G. and Li, X. S. 2004. Sand plasticity
model accounting for inherent fabric anisotropy.
Journal of
Engineering Mechanics
, ASCE, 130(11), 1319-1333.
Gudehus, G. and Nübel, K. 2004. Evolution of shear bands in sand.
Géotechnique
, 54(3), 187-201.
Lancellotta, R. 2002. Analytical solution of passive earth pressure.
Géotechnique, 52(8), 617-619.
0
A,cr
Cp
C
0
A,min
A,cr
2
Cp
C
0
A,min
A,cr
A,min Cp
2
(2)
K K
u u
K K
K
u
u
K K
K K u
Leśniewska, D. & Mróz, Z. 2001. Study of evolution of shear band
systems in sand retained by flexible wall.
International Journal for
Numerical and Analytical Methods in Geomechanics
, 25, 909-932.
K
Loukidis, D. and Salgado, R. 2009. Modeling sand response using two-
surface plasticity.
Computers and Geotechnics
, 36(1-2), 166-186.
where
u
Cp
is the crest displacement needed to reach MPS. Based
on the previous discussion,
u
Cp
can be taken equal to 0.005
H
.
The characteristic values of the active earth pressure
coefficient,
K
A,min
and
K
A,cr
, can be calculated using the
Coulomb’s equation (Eq. 1) with suitable (equivalent) values
eq
for the mobilized friction angle inside the sliding wedge. In
Fig. 7, we see that there is a linear dependence between
eq
for
MPS and
c,TX
, which can be expressed by
Loukidis, D., Chakraborty, T. and Salgado, R. 2008. Bearing capacity of
strip footings on purely frictional soil under eccentric and inclined
loads.
Canadian Geotechnical Journal
, 45(6), 768-787.
Manzari, M.T. and Dafalias, Y.F. 1997. A critical state two-surface
plasticity model for sands.
Géotechnique
, 47(2), 255-272.
Soubra, A-H and Macuh, B. 2002. Active and passive earth pressure
coefficients by a kinematical approach.
Proceedings of the
Institution of Civil Engineers – Geotechnical Engineering
, 155(2),
119-131.
Vardoulakis, I. 1980. Shear band inclination and shear modulus of sand
in biaxial tests.
International Journal for Numerical and Analyrical
Methods in Geomechanics
, 4(2), 103-119.
(MPS)
R
eq
c,TX
35
7 (3)
100%
o
D
We consider
c,TX
instead the more physically suitable
c,PS
because it is easier to estimate through empirical relationships,
measurements of the angle of repose on a conical soil heap, or a
few triaxial compression tests. On the other hand, to calculate
K
A,cr
, the friction angle can be estimated using


