1957
Technical Committee 207 /
Comité technique 207
2.4.2
Fonctions de transfert
Ces fonctions de transfert sont utilisées pour caractériser la
mobilisation des cisaillements interne (τ
int
) et externe (τ
ext
) ainsi
que les réactions en pointe. On utilise pour cela les lois
bilinéaires du type proposé par Frank et Zhao (1982)
caractérisées par deux paramètres : un paramètre de pente (
K
t
ou
K
p
) et une valeur de contrainte limite (
q
s
ou
q
p
).
Pour le cisaillement interne et la mobilisation des réactions
en pointe, ces lois sont construites directement à partir des
paramètres pressiométriques.
Pour le cisaillement extérieur τ
ext
, la valeur de contrainte
limite q
s
peut être reliée à la contrainte verticale dans le sol non
renforcé σ
v0
’ par une relation du type q
s
= ktan
.σ
v0
’. Les
valeurs choisies pour q
s
et le paramètre de pente peuvent être
ajustés de manière à retrouver par le modèle du type exposé,
appliqué au cas d’une inclusion de section nulle, un tassement
identique à celui de la semelle superficielle rigide sur sol non
renforcé calculé par la méthode pressiométrique (Frank, 1999).
3
APPLICATION SIMPLE : CAS D’UNE SEMELLE SUR
UNE SEULE INCLUSION
3.1
Paramètres d’entrée
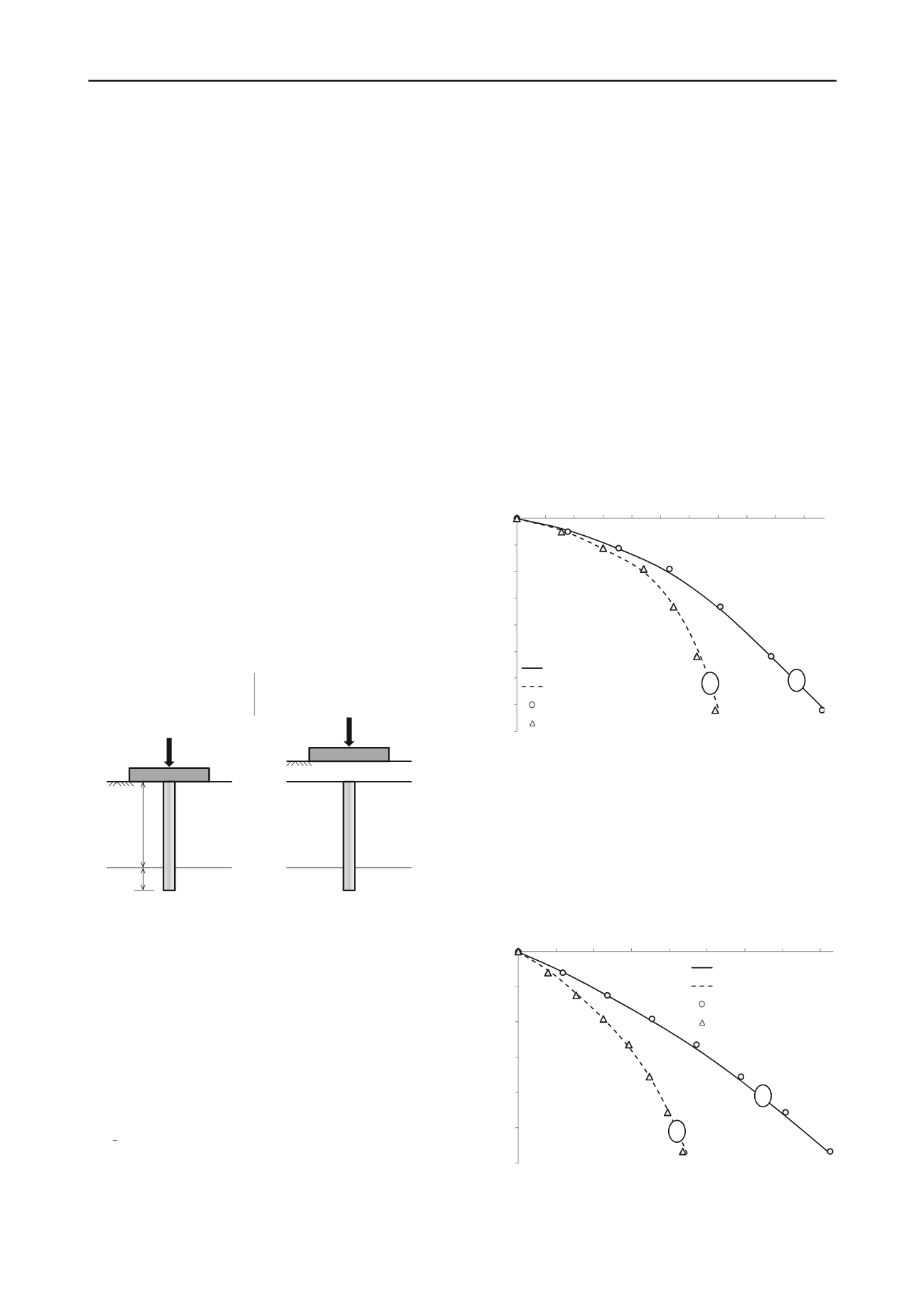
L’exemple étudié est celui d’une semelle carrée de 1,33 m de
côté, renforcée par une seule inclusion de diamètre 40 cm
placée dans l’axe. Deux situations sont étudiées : le cas d’une
semelle en contact direct avec l’inclusion (mode
« fondation mixte »), et le cas d’une couche de forme
intercalaire de 50 cm d’épaisseur (mode « inclusion rigide »).
La figure ci-dessous présente la coupe du calcul et les données
géotechniques utiles.
Q
Horizon meuble
E = 6 MPa, E
M
= 3 MPa
q
s
= 30 kPa, φ’ = 30°
Q
Couche de forme (E = 50 MPa)
Horizon porteur
E = 120 MPa, E
M
= 20 MPa
q
s
= 120 kPa, q
p
= 3,5 MPa
φ’ = 30°, c’ = 50 kPa,
6,5 m
0,5 m
Mode
« fondation mixte »
Mode
« inclusion rigide »
Figure 4. Cas d’une semelle sur une seule inclusion - Coupe de calcul.
Dans le cas d’une maille unique, le paramètre β est pris égal
à 1,00 : le cisaillement extérieur avec le massif de sol non
renforcé se développe sur tout le périmètre. Les fonctions de
transfert sont constituées selon la démarche décrite en §2.4.2 :
en particulier, pour le cisaillement extérieur, le calage du
paramètre de pente
K
t
conduit à une valeur équivalente de
K
t
=
2,7 MPa/m. Pour le mode « inclusion rigide », le domaine
inclusion est prolongé dans le matelas : la loi d’interface entre
les domaines inclusion et sol sur la hauteur du matelas est
construite en considérant un module pressiométrique E
M
= 10
MPa et un frottement unitaire limite égal à ktanδ.σ
s
avec ktanδ
= 1 et σ
s
la contrainte verticale moyenne dans le domaine sol,
sur la hauteur du matelas.
Les résultats du calcul sont comparés à ceux d’un traitement
en éléments finis sous PLAXIS (modèle axisymétrique
équivalent). Dans ce modèle, tous les sols ont un comportement
élasto-plastique parfait avec un critère de rupture de Mohr
Coulomb : les paramètres d’entrée sont ceux de la Figure 4. Le
choix des paramètres, et notamment ceux décrivant le
comportement en pointe (module de déformation et paramètres
de cisaillement), a été validé au préalable par calage des courbes
de chargement axial d’une inclusion isolée chargée directement
en tête (sans semelle), calculées respectivement par un modèle
PLAXIS ou un modèle analytique à l’aide des lois de Frank et
Zhao.
3.2
Sans matelas de répartition : mode « fondation mixte »
La première situation étudiée est celle d’un contact direct entre
la semelle et l’inclusion (fondation mixte). Une partie de la
charge totale Q appliquée sur la semelle est reprise par le sol,
mais le frottement mobilisé sur la hauteur de l’inclusion
demeure positif : la charge maximale dans l’inclusion est
obtenue en tête. La figure ci-dessous présente les résultats
obtenus selon un diagramme Effort – Tassement. Deux courbes
sont représentées : celle du tassement de la semelle en fonction
de la charge appliquée (Courbe 1), et celle du tassement de la
semelle (= tassement en tête de l’inclusion) en fonction de
l’effort maximal dans l’inclusion (Courbe 2). Les résultats se
révèlent en bon accord avec ceux de PLAXIS.
0
5
10
15
20
25
30
35
40
0 100 200 300 400 500 600 700 800 900 1000 1
Tassement (mm)
Effort (kN)
PLAXIS - Q_semelle
PLAXIS - Qmax-Inclusion
Analytique - Q_Semelle
Analytique - Qmax_Inclusion
1
2
Figure 5. Effort sur la semelle et effort maximal dans l’inclusion en
fonction du tassement en tête - cas d’une fondation mixte.
3.3
Avec matelas de répartition : mode « inclusion rigide »
Dans cette situation, une couche de forme sépare la semelle de
l’inclusion. La principale différence avec le cas précédent est
l’apparition d’un frottement négatif : l’effort maximal dans
l’inclusion n’est pas obtenu en tête mais au niveau du plan
neutre identifié ici vers 1,0 m de profondeur. La même
concordance peut être observée avec PLAXIS.
0
10
20
30
40
50
60
0
150 300 450 600 750 900 1050 1200
Tassement (mm)
Effort (kN)
PLAXIS - Q_semelle
PLAXIS - Qmax_Inclusion
Analytique - Q_Semelle
Analytique - Qmax_Inclusion
1
2
Figure 6. Effort sur la semelle et effort maximal dans l’inclusion en
fonction du tassement en tête du modèle- cas d’une inclusion rigide.


