1956
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
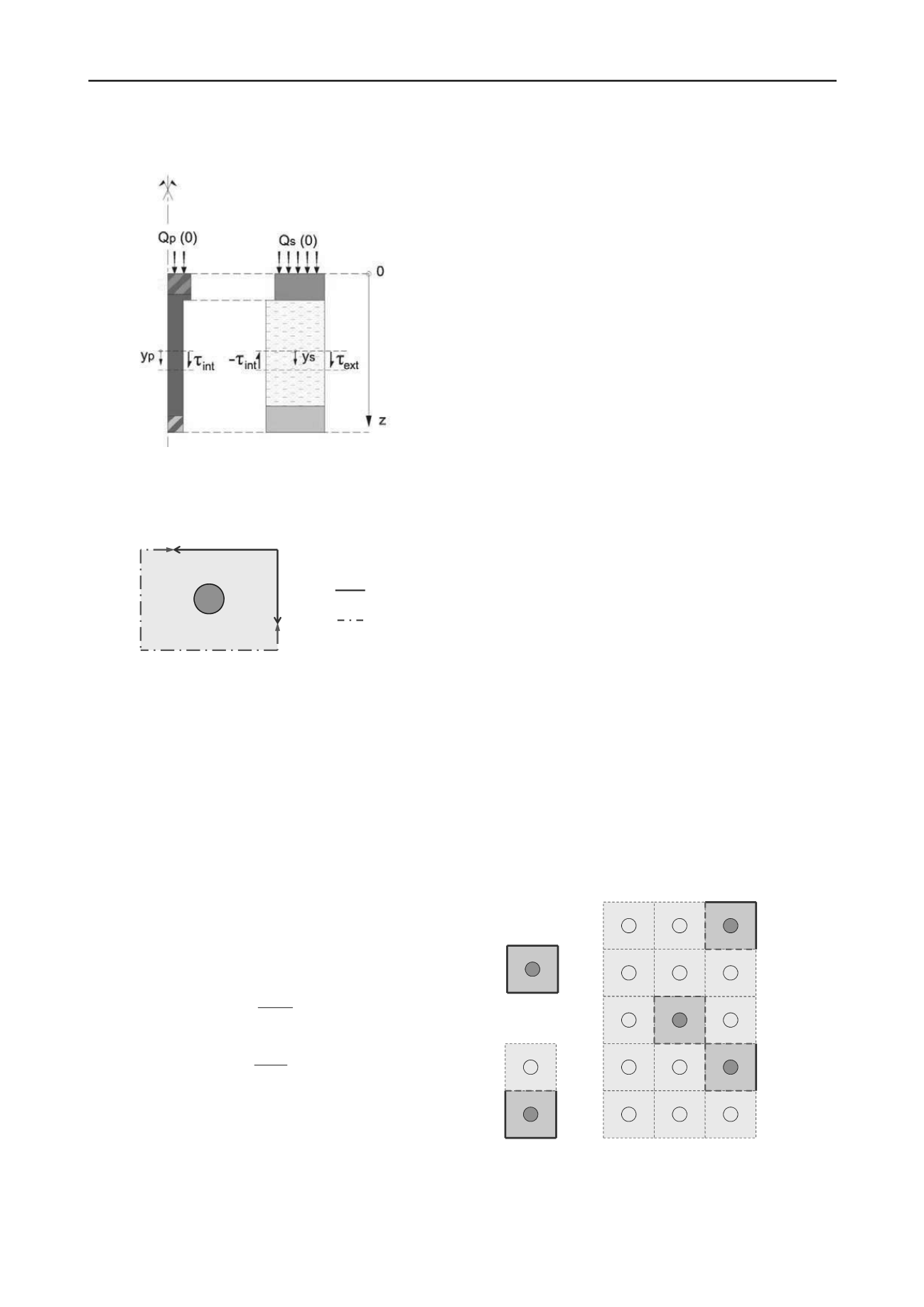
par un cisaillement vertical extérieur τ
ext
comme le schématise
la figure ci-dessous.
Figure 1. Modèle généralisé de la cellule élémentaire – vue en coupe.
Le cisaillement extérieur τ
ext
est supposé se développer sur
une fraction β x P
ext
(0 ≤ β ≤ 1) du périmètre extérieur total P
ext
de la cellule comme le schématise la figure ci-dessous.
β x P
ext
(1-β) x P
ext
P
int
τ = τ
ext
τ = 0
Figure 2. Modèle généralisé de la cellule élémentaire – vue en plan.
Les deux domaines sont assimilés à deux cylindres
concentriques de sections équivalentes. On désigne par S
p
(z) la
section du domaine « inclusion » à la profondeur z. La section
du domaine « sol » s’en déduit à l’aide de la relation : S
s
(z) =
S
maille
– S
p
(z) où S
maille
désigne l’aire totale de la maille.
2.2
Mise en équation
On désigne par y
p
(z) et y
s
(z) les tassements respectifs des
domaines « inclusion » et « sol ». La combinaison des équations
d’équilibre et de comportement des cylindres équivalents aux
deux domaines conduit au système d’équations (1), où E
p
(z) et
E
s
(z) représentent respectivement les modules de déformation
verticale des domaines « inclusion » et « sol ». Pour le domaine
« sol », le tassement y
s
(z) est supposé uniforme à toute
profondeur z et E
s
(z) est assimilé au module équivalent pour
l’amplitude de chargement calculée.
ext
ext
s
s s
p
p p
P
P
dz
yd
SE
P
dz
yd
SE
.
sol
Domaine
inclusion
Domaine
int
int
2
2
int
int
2
2
(1)
L’interaction entre les deux domaines est décrite au niveau
de chaque couche par une fonction de transfert exprimant la
dépendance du cisaillement τ
int
avec le déplacement relatif entre
les deux domaines :
s
p
y yf
int
(2)
L’interaction éventuelle entre la cellule et le sol environnant
non renforcé est décrite par une fonction de transfert reliant le
cisaillement extérieur τ
ext
au déplacement absolu du domaine
sol :
s
ext
yf
(3)
La combinaison des équations (1), (2) et (3) conduit à un
système global à 4 équations et 4 inconnues : y
p
, y
s
, τ
int
, et τ
ext
.
2.3
Résolution
Le système précédent est complété par les conditions aux
limites suivantes :
-
charge totale appliquée en tête du modèle Q
p
(0)+Q
s
(0);
-
fraction de cette charge transmise en tête du domaine
inclusion E
QP
= Q
p
(0)/[Q
p
(0)+Q
s
(0)] ;
-
loi de mobilisation de l’effort de pointe avec le
déplacement relatif.
En présence d’un élément de fondation rigide en surface
(radier ou semelle), la valeur de E
QP
est établie en recherchant
l’égalité des tassements en surface y
p
(0)
et y
s
(0), ce qui est
justifié par le fait que les déformations de l’élément structurel de
surface sont négligeables devant celles du sol.
La résolution numérique du système est menée à l’aide d’une
formulation en éléments finis. Chacun des deux domaines est
discrétisé selon un maillage unidimensionnel avec des éléments
à deux nœuds et un degré de liberté par nœud. Dans le cadre de
cette discrétisation, le système d’équations précédent s’écrit
sous la forme d’un système matriciel équivalent, ce qui en
simplifie la résolution. La non-linéarité des courbes de transfert
implique une procédure itérative visant à assurer la
compatibilité en tout point entre cisaillement et déplacement.
2.4
Mise en œuvre pratique
2.4.1
Choix du paramètre β
L’introduction du paramètre β dans le modèle de la cellule
élémentaire permet d’aller au-delà de la configuration
particulière d’une maille courante où les conditions de symétries
justifient l’hypothèse d’un cisaillement nul en périphérie du
modèle (β = 0). Le choix d’un β ≠ 0 implique la prise en compte
d’un cisaillement extérieur entre la cellule et le sol environnant
non renforcé, sur une partie du périmètre extérieur de la cellule.
Dans le cas d’une maille carrée (figure ci-dessous), cela peut
être par exemple représentatif d’une cellule située au bord du
massif renforcé (β = 0,25), le cas d’une cellule située à l’angle
(β = 0,5), le cas d’une semelle sur deux inclusions (β = 0,75) ou
une inclusion unique (β = 1).
β = 0,5
β = 0
β = 0,25
β = 0,75
β = 1
Figure 3. Choix du paramètre β pour le cas d’une maille carrée.


