1552
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
50mm in diameter and 200mm in height and subjected to a
vertical pressure of 50 kPa. After consolidation, a specimen
measuring 5 cm in diameter and 10 cm in height was formed.
To prepare specimen from samples with an Iwakuni clay
content 17% or less, the soil mixtures were placed in a mold in
5 layers with each layer being compacted using a steel rammer
with a prescribed number of blows. The compaction energy, E
c
,
was calculated as follows (Adachi et al., 2000):
(1)
where, W
R
is the rammer weight (=0.00116 kN), H is the drop
height (m), NL is the number of layers (=5), N
B
is the number
of blows per layer, and V is the volume of mold (m
3
). Various
compaction energies, E
c
, were obtained by changing H and N
B
.
Each soil mixture was thoroughly mixed at an initial water
content of w=11%. Given that the initial water content of a
compacted soil sample does not change the properties of the
clay, the water content was selected to allow the free passage of
carbon dioxide. In order to improve the specimen saturation,
carbon dioxide was first passed through the specimens before
allowing water to percolate.
In this research, soil samples with fines content
F
c
=0, 9.8,
14.7, 16.7% were formed at constant compaction energies,
corresponding to
E
c
=22, 51, 113, 324, 504, 1008 kJ/m
3
, and at
constant relative densities of sand structure, i.e.,
D
r
sc
=0, 30, 50,
65%. (Table.1)Note that for soil samples prepared under
compaction energies of
E
c
=504 and 1008 kJ/m
3
, the variation of
granular void ratios with fines content is practically similar;
therefore, considering the rammer used in the sample
preparation, relative densities of the sand-clay mixtures cannot
be changed even with higher compaction energies. Thus, the
granular void ratios corresponding to these compaction energies
can be considered as the minimum granular void ratios in these
experiments.
As mentioned earlier, for soil samples with fines contents
greater than
F
c
=19.6%, sample preparation by compaction was
not possible; instead, the pre-consolidation method was
employed. Depending on the normal consolidation condition,
the granular void ratio of the pre-consolidated sample is unique
for a given effective confining pressure.
2.3 Skeletal structure of sand-clay mixture
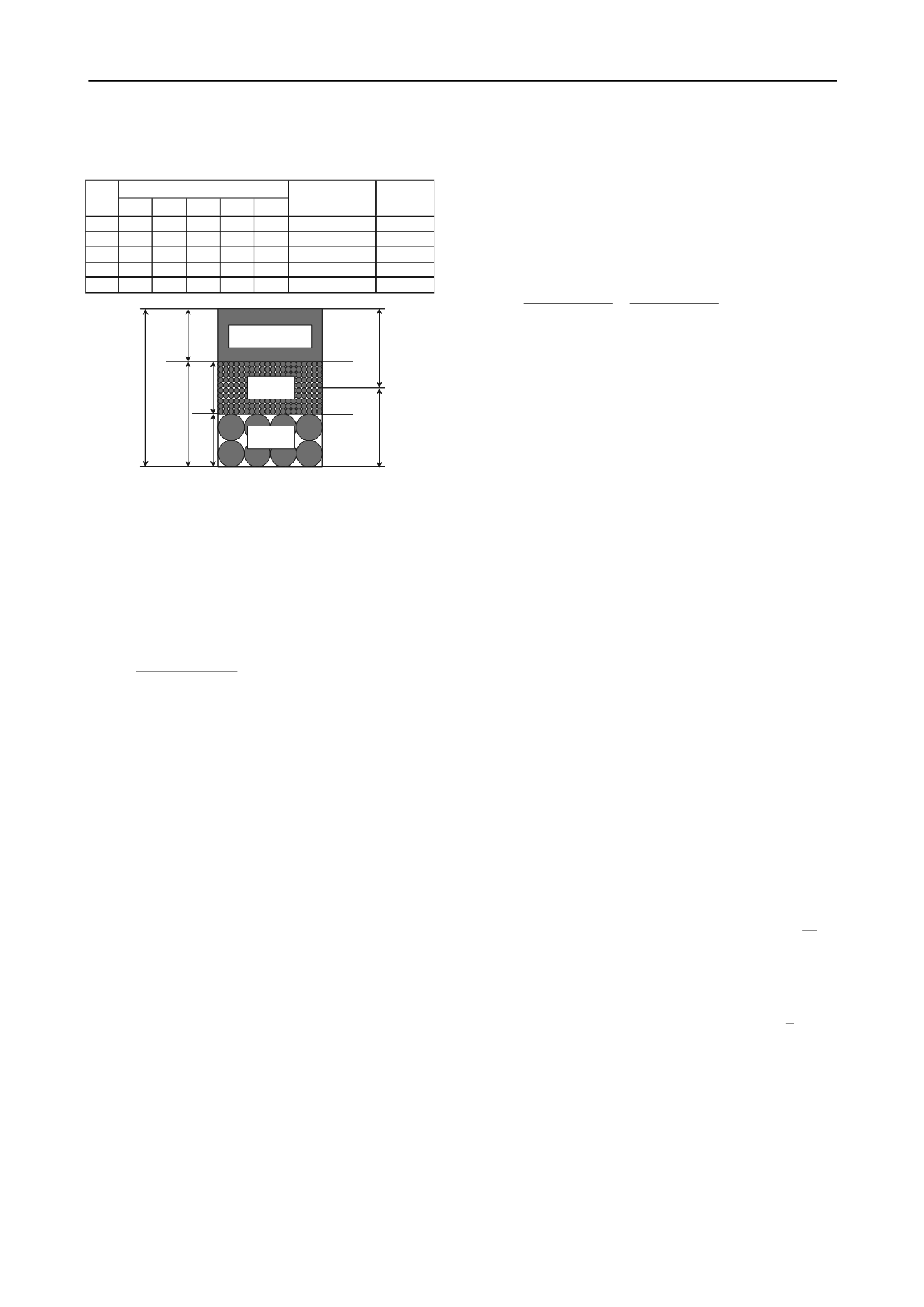
A fully saturated sand-clay mixture has a three-phase
composition, namely the coarse-grained particles, fine-grained
particles and pore water, as shown in Fig. 2. Here,
b
is defined
as the portion of fines that contributes to the active intergrain
contacts. In Thevanayagam et al. (2002), it was introduced to
represent the beneficial secondary cushioning effect of silica
silts in silty sand as follows:
(2)
where
e
ge
is the equivalent granular void ratio,
F
c
is the
fines content (in terms of volume) and b denotes the portion of
the fines that contributes to the active intergrain contacts.
Basically,
b
=0 means that none of the fine grains actively
participates in supporting the coarse-grain skeleton (i.e. the
fines act exactly like voids); and
b
=1 implies that all fines
actively participate in supporting the coarse grain skeleton
(i.e. the fines are indistinguishable from the host sand
particles). The magnitude of
b
depends on grain size disparity
and grain characteristics.
3 UNDRAINED CYCLIC SHEAR PROPERTIES
The specimens of sand-clay soil mixtures prepared by
compaction and pre-consolidation methods were isotropically
consolidated at an effective confining pressure of
c
’=100 kPa.
Then, undrained cyclic triaxial tests were conducted with
effective confining pressure
c
’=100 kPa and loading frequency
f=0.02Hz using an air pressure controlled cyclic triaxial test
apparatus.
Fig. 3 shows the relationship between the cyclic shear
strength ratio (σd/2σc’) required to cause double amplitude
axial strain ε
DA
=5% and the number of cycles (N) for soil
specimens with fines mixtures (Iwakuni clay).
Based on Fig.
3(a), for specimens prepared under high compaction energy
E
c
=504 kJ/m
3
, the liquefaction strength decreases as the fines
content increases, with the liquefaction strength of specimens
with
F
c
=14.7% significantly smaller than those of specimens
with
F
c
=0% and 9.8%. On the other hand, for specimens
prepared under a low compaction energy
E
c
=22 kJ/m
3
(Fig.
3(b)), although the difference between the liquefaction curves of
various samples are small, there is a tendency for the
liquefaction strength to increase with an increase in fines
content.
Next, the results of specimens prepared under constant
fines content
F
c
=0% (Fig. 3(c)) shows that the liquefaction
strength increases as the compaction energy increases, with the
liquefaction strength of specimen with
E
c
=22, 51 kJ/m
3
significantly smaller than those of specimens with
E
c
> 113
kJ/m
3
. On the other hand, for specimens prepared under
constant fines content
F
c
=16.7% (Fig. 3(d)), it is also observed
that there is increase in strength as the compaction energies
increased. However, the liquefaction strengths show almost
similar values.
Fig. 3(e) shows the result of the pre-
consolidation samples for Iwakuni clay mixtures (
F
c
>19.6%).
The cyclic shear strength ratios increase with fines content.
However, in this case the liquefaction strengths show almost
similar values (
F
c
>29.4%).
The cyclic shear strength corresponding to 20 cycles
(hereinafter referred to as cyclic shear strength ratio,
R
L(N=20)
) is
read off from the above curves and plotted against the fines
content for Iwakuni clay mixtures, as shown in Fig. 4.
A
t
constant relative density of sand structure, on the other hand,
any increase in fines content results in an increase in cyclic
strength. This can be explained as follows. In the case of
constant relative density of sand structure, more fines will
occupy the voids between the sand particles when the fines
V
NNHW E
B L
R
c
sf
s
sf
v
sf
v
V
e
sf
ss
eq
b
V
Vb
V
bV V
Vb
V
) 1(
) 1(
) 1(
1st
2nd 3rd 4th 5th
504 60 80 100 120 140
0.184
0.00116
324 40 50 65 75 85
0.184
0.00116
113 14 19 23 25 29
0.184
0.00116
51 4 7 10 13 16
0.184
0.00116
22 5 10 15 25 30
0.050
0.00116
Number of dropping per a layer
E
c
(kJ/m
3
)
Height of dropping
weight
(m)
Weight of
rummer
(kN)
Table. 1
Relation between dropping number and
compaction energy
e
ge
V
v
=
e
V
s
=1
V
sf
V
V
ss
(1-
b
)
V
sf
Void
Fines
Sand
1
b
・
V
sf
Fig. 2 Phase diagram


