1025
Technical Committee 105 /
Comité technique 105
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
1) Set-up the geometry of the walls and floor of the container
and the elements on the floor where the contact stresses
will be monitored and the details of the trapdoor as shown
on the left hand side Figure 1. The trapdoor is 150 mm
long and 150 mm wide and consists of three elements 50
mm long by 150 mm wide. The walls and floor of the
container are assumed to be rigid.
The normal and tangential stiffnesses between the floor
elements and the spherical particles are the same as those
of between the spherical elements. The friction coefficient
between the spherical particles and the floor elements is
0.5, which is the same as that between the particles.
2) Generate the spherical elements above the floor in the upper
part of the container to a depth of 150mm. Calculations
are repeated under gravity loading until the displacement
rates of the spheres approach zero and the bed has come
to equilibrium. Knowing the maximum and minimum
void ratios of Toyoura sand, the relative density of the
sand bed was estimated to be 86%.
3) To simulate the trapdoor tests, the trapdoor was lowered at a
constant displacement rate of 5mm/sec. The vertical
stresses on the trapdoor and the floor next to the trapdoor
were calculated.
For the gravity flow simulations, the trapdoor was
removed instantaneously and dynamic vertical stresses on
the floor next to the trapdoor were calculated.
3 RESULTS AND DISCUSSION
First, the experimental data is compared with the DEM analysis
data in the trapdoor tests and then the gravity flow simulation is
discussed.
3.1
Trapdoor tests
Figure 2 shows the variation of vertical stress,
p
, on the trapdoor
against the downward displacement,
d
t
, and on the floor
elements adjacent to the trapdoor. The depth of the sand layer
was 150 mm, equal to the width of the trapdoor; the initial
vertical pressure on the floor of the container was 2.38kN/m
2
.
The plots compare the experimental data obtained by Kikumoto
et al (2003) with the calculated DEM values. The centre of
elements A, B and C are respectively 150mm, 300mm and
450mm from the centre of the trapdoor. It is seen that the
vertical stress adjacent to the trapdoor is affected by the
trapdoor movement but further away the influence of the
movement is negligible. The vertical stress on the trapdoor
rapidly decreased at the onset of the downward movement, and
the experimental and DEM values corresponded well. The final
value when
d
t
= 2.0mm is 0.62kN/m
2
for the DEM results. On
the other hand, the vertical stress on element A increased
rapidly with the lowering of the trapdoor and then settles to a
constant value of 3.0kN/m
2
in the DEM. The initial rate of
increase for the vertical stress for element A in the DEM results
is different from that of the experimental data. This reason is not
clear, but it may be related to the difference in dilation rate
between Toyoura sand and spherical DEM elements.
The vertical stresses on floor elements B and C increased
slightly and there is good agreement between the experimental
data and the calculated DEM results.
Figure 3 shows the distribution of vertical stress laterally
from the centre of the trapdoor when
d
t
= 2.0mm. The vertical
stress on the trapdoor decreased and increased on the floor next
to the trapdoor. The DEM data show a sawtooth distribution not
seen in the experimental data.
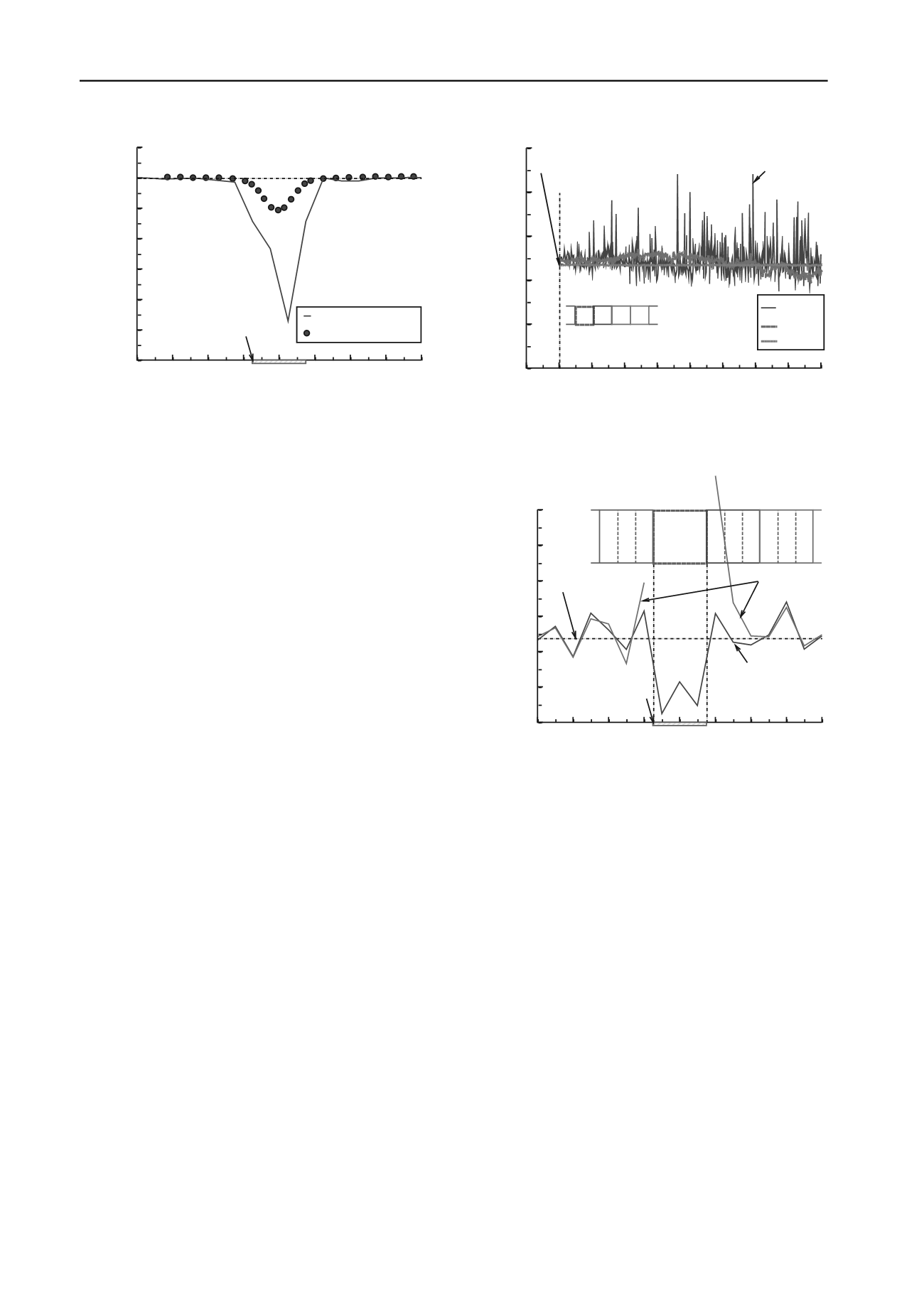
Figure 4 shows the surface settlement of the sand above the
centre of the trapdoor when
d
t
= 2.0mm at the depth of the sand
layer was 150 mm. The experimental data was measured by the
laser displacement scanner which accuracy was 1
m (Kikumoto
et al. 2003). It is, however, Figure 4 that reveals the most
significant shortcoming of the DEM modelling as the
experimental and calculated subsidence trough at the upper
surface of the sand are very different; the surface settlement in
-400 -300 -200 -100 0 100 200 300 400
0
1
2
3
4
5
6
Earth pressure,
p
(kN/m
2
)
Horizontal distance from the centre of trapdoor,
h
d
(mm)
DEM (trapdoor)
DEM
(gravity flow)
gravity flow
initial earth pressure
(=2.38kPa)
trapdoor
t
=0.3sec
Figure 4. Surface settlement of the sand above the centre of the
trapdoor when
d
t
= 2.0mm, layer thickness 150 mm.
Figure 5. Vertical stress on the floor next to the trapdoor during
gravity flow.
Figure 6. Comparison of vertical stress distributions on the floor
next to the trapdoor during trapdoor lowering and during gravity
flow at the elapsed time of 0.3sec.
-0.05 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40
0
1
2
3
4
5
Earth pressure,
p
(kN/m
2
)
Elapsed time after the trapdoor deleted,
t
(sec)
C (DEM)
B (DEM)
A (DEM)
gravity flow
A B C
initial earth pressure 2.38kPa
t
=0.3sec
-400 -300 -200 -100 0 100 200 300 400
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-0.5
Surface settlement,
s
s
(mm)
Horizontal distance from the centre of trapdoor,
h
d
(mm)
Kikumoto et al. 2003
DEM
trapdoor


