1004
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
presented in De Larrard (2000), this paper present only a
succinct description.
2.1.1 Compacity of granular mixtures
For binary mixtures with grain size
d
1
and
d
2
three cases could
be considered depending upon the interaction between the two
types of grains: no interaction, full interaction and partial
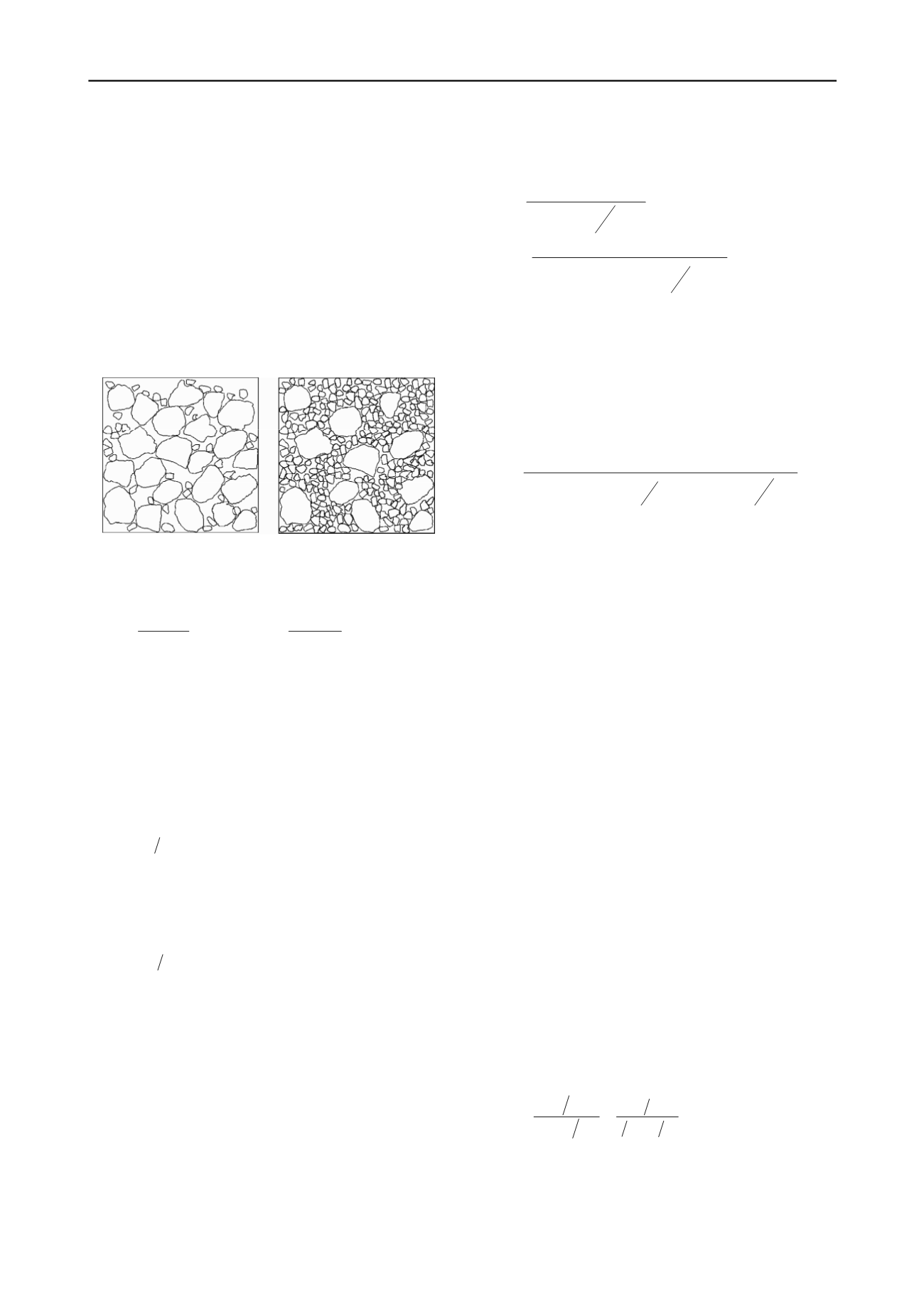
interaction. Figures 1(a) and 1(b) illustrates the case of a binary
mixture with no interaction between particles. For this case the
virtual compacity
could be obtained knowing the volumetric
concentration,
y
1
and
y
2
, and the residual compacity,
1
and
2
,
of each class size as follows:
The total volume is:
(2)
1
2
1
y y
(a) (b)
Figure 1. Case of binary mixtures with no interaction.
The partial volume of each class
is the volume of the class
in the unit volume, then:
2
1
1
1
y
and
2
1
2
2
y
(3a, b)
The virtual compacity for a binary mixture becomes:
2
1
(4)
When the bigger grains are dominant, the virtual compacity
is
1
. In this case, the bigger grains fill up the volume with no
interaction with the small grains. For this reason the partial
volume
1
is the same than the residual compacity
1
, so
1
1
. Then accordingly with equations 2 to 4, the virtual
compacity
1
becomes:
)
1(
2
1 1
y
(5)
When the smaller grains are dominant the virtual compacity
is
2
. In this case the smaller grains fill the voids existing
between the bigger grains with their maximum individual
compacity
2
. In this case the virtual compacity
2
is:
1 2
2
2
1 1
y
(6)
For the binary mixture only one virtual compacity is
possible, this compacity is the minimum between
1
and
2
. In
fact if
is higher than
1
grains 2 penetrate into grains 1 and
vice versa. For this reason the only possible arrangement
correspond to the minimum virtual compacity. This condition is
called the impenetrability condition:
2 1
,
inf
(7)
Different interactions between particles can be considered: a
binary mixture having total interaction occurs when the size of
the particles is identical but the residual compacities are
different:
2
1
;
d d
2
1
. On the other hand, for the case of
binary mixtures with
d
1
>
d
2
two physical effects could appear:
de-compaction effect and boundary effect. Taking in to account
these two effects, De Larrard (2000), calculate the virtual
compacity
1
and
2
as follows:
2 2
1 12
1
1
1 1
y
a
(8)
1 1
2 21 2
2
2
1 1
1 1
y
b
(9)
Where
a
12
is the de-compaction coefficient and
b
12
is the
boundary effect coefficient.
In the case of a poly-disperse mixture with n
c
granular
classes and with
d
1
>
d
i
>
d
nc
, the grains
d
>
d
i
in the mixture
undergo a de-compaction effect due to the grains which size
d
<
d
i
and the mixture undergo a boundary effect due to the
grains which size is
d
<
d
i
. The virtual compacity, considering the
grain size
i
as the dominant grains is, (De Larrard, 2000):
1
1
1
1
1 1
1 1
i
j
n
i j
j
j
i
ij
j
j
i
ij
i
i
i
y
a
y
b
(9)
Similar than the case of binary mixtures, the impenetrability
restriction is applicable. This restriction becomes:
i
ni
inf
1
(10)
Once calculating
i
considering each class
i
as the dominant
class (using equation 10), the actual dominant grain size is the
one for which the minimum
i
is obtained. From the
geotechnical point of view, all the grains with
d
<
d
i
are the
matrix of the mixture, and the grains with
d
>
d
i
are dispersed
grains in the mixture. The virtual compacity
is unreachable
experimentally. For this reason it is necessary to obtain the
actual compacity,
, which is more or less close to the virtual
compacity depending upon the compaction method (
<
). For
a real mixture the compacity
is the accumulation of the
compacitys corresponding to each class:
n
i
i
1
(11)
In the mixture the dominant grain has the maximum
compacity, taking in to account the presence of the other grains,
this compacity is
i
.Therefore the compacities in the mixture
are:
....
,
,
.......
.
*
*
0
1
i
i
1
i
n
To obtain the relationship between the virtual compacity and
the actual compacity, De Larrard, 2000, proposes a compaction
coefficient
K
. This compaction coefficient is the addition of the
compaction coefficient corresponding to each grain size:
n
i
i
K K
1
(12)
The compaction coefficient for each grain size is obtained as
follows:
i
i
i
i
i
i
i
i
y
K
1 1
1
*
*
(13)
2.2 Probability of crushing of particles depending on its
compacity
The relationship
i
/
i
*
is a powerful parameter to assess the
stress level supported by the particles of size
d
i
within the
granular material. In fact,
i
is the volume filled by the


