796
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
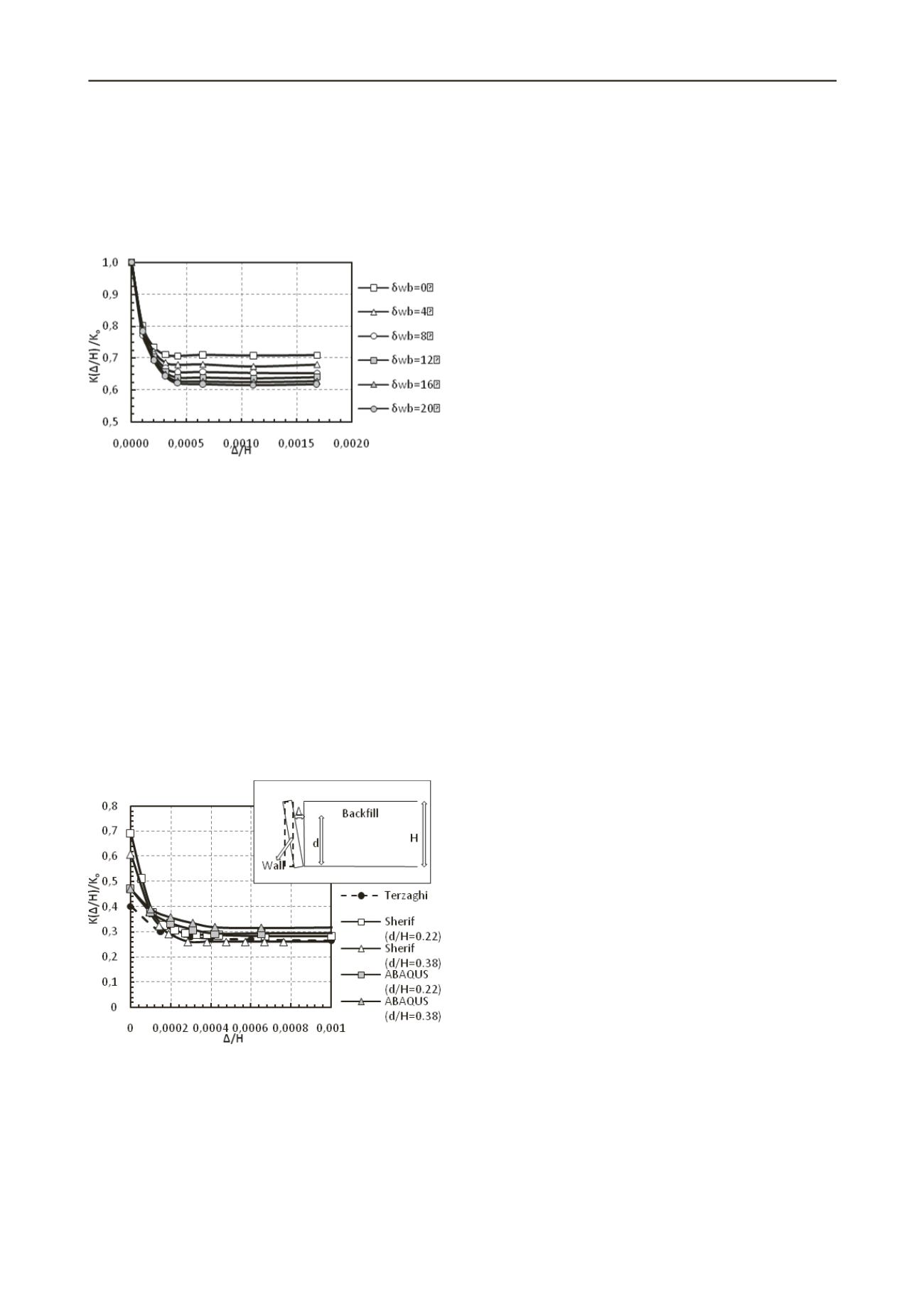
In Figure 10, the impact of
wb
on the mobilization of an
active state with wall movement is presented. While the results
show that increasing wall friction leads to reduced lateral
stresses, there is no substantial effect on the amount of wall
displacement required to mobilize an active condition. Similar
to Figure 7, an active failure condition is mobilized at about
=
0.0004H.
Figure 10: Effect of wall movement and
wb
on the mobilization of
K(
Δ
/H)/K
0
for retaining walls with
sb
= 32
o
and
sw
= 15
o
Figure 11: Effect of wall movement on horizontal stress reduction and
the mobilization of an active condition based on the numerical analyses
of this study and the experiments of Terzaghi (1934) and Sherif et al.
(1984)
4 COMPARISON WITH PHYSICAL MODEL TESTS
Figure 11 compares the finite element analyses of this study
with the lateral earth pressures from physical model tests
(Terzaghi 1934; Sherif et al. 1984). Comparisons are made with
Sherif et al. (1984) results at the depths of soil pressure gages
SP5 (depth/wall height = 0.22) and SP4 (depth/wall height =
0.38), whereas the lateral earth pressure coefficient from the
overall earth pressure diagram is used for presenting Terzaghi
(1934) data. Note that the lateral stresses from the finite element
analyses are for walls moving horizontally, while Terzaghi
(1934) and Sherif et al. (1984) experiments were conducted on
walls rotating about their base. Accordingly, wall displacement
(
Δ
) corresponds to the displacement measured at wall’s mid-
height for Terzaghi (1934) experiments, and is calculated from
the amount of wall rotation at the corresponding depths for
Sherif et al. (1984) experiments.
According to Figure 11, lateral stresses and their rate of
reduction decrease with wall displacement in all studies.
However, the initial rate of lateral stress reduction is the largest
in Sherif et el. (1984) experiments, followed by the finite
element analyses and Terzaghi’s experiments. As a result, the
active state is reached at smaller displacements (
Δ
= 0.0003H)
in Sherif et al.’s experiments, followed by
Δ
= 0.0004H in the
finite element analyses, and Terzaghi’s experiments at
Δ
=
0.001H – 0.002H. These displacement are smaller than that (
Δ
=
0.004H) suggested by Clough and Duncan (1991) for reaching
an active state in loose sands. Although the active stresses are
more-or-less similar in all studies, the initial lateral stress
coefficients are broadly different, which could likely be due to
differences in backfill soil density and friction angle. Note that
both Sherif et al. (1984) and Terzaghi (1934) report linear
distributions for the active stress diagrams behind walls rotating
about their base. While the effect of backfill soil arching is
discussed in this study, we suspect that the difference in wall’s
mode of movement (rotation versus horizontal movement)
could be the reason for not seeing arching in the physical model
tests.
5 CONCLUSIONS
In this paper, the lateral earth pressure acting on a rigid
retaining wall was studied using the finite element analysis
method. The results of the simulations showed that the true
earth pressure distribution is non-linear mainly due to soil
arching effect at deeper levels and backfill-subsoil interaction to
a lesser extent. The results indicated that the influence of
backfill arching increases with wall displacement and backfill
subsoil friction while increasing friction between the backfill
and wall or subsoil and wall has no substantial effect on
arching. The results were compared with those from physical
model tests of Terzaghi (1934) and Sherif et al (1984). The
results of these simulations showed that an active state is
mobilized at wall displacements smaller than those suggested
by the Terzaghi’s physical model experiments but larger than
those suggested by Sherif et al. (1984). The outcomes of this
study further indicate that by increasing backfill-subsoil
friction, the active state becomes mobilized at smaller wall
displacements. The results also showed that although increasing
wall-backfill interface friction leads to reduced lateral stresses,
this has no effect on the wall displacement required to mobilize
an active condition.
6 REFERENCES
ABAQUS Users Manual, version 6.10. 2010. Hibbitt, Karlsson and
Sorenson Inc., Pawtucket, R.I.
Been, K., and Jefferies, M. (2004). “Stress-dilatancy in very loose
sand.” Canadian Geotechnical Journal, 41: 972 – 989.
Clough, G.W. and Duncan, J.M. 1991. Earth pressures.
Foundation
engineering handbook
. 2nd ed. (H.Y. Fang, ed.) Van Nostrand
Reinhold, New York, NY. pp. 223 - 235.
Coulomb, C.A. 1776. Essai sur une application des re`gles des maximis
et minimis a` quelques proble`mes de statique relatifs a`
l’architecture. In
Me`moires Acade`mie Royale Pre`sente´s par
Divers Savants
, Paris. Vol. 7, pp. 343–382.
Jaky, J. 1944. The Coefficient of Earth Pressure at Rest.
Journal of the
Society of Hungarian Architects and Engineers
, Budapest,
Hungary, pp. 355.
Manzari, M.T., and Dafalias, Y.F. 1997. A critical state two-surface
plasticity model for sands. Géotechnique, 47(2): 255–272.
Mei, G. Chen, Q. and Song, L. 2009. Model for predicting
displacement-dependent lateral earth pressure.
Can. Geotech. J
. 46:
969–975 (2009).
Rankine, W.J.M. 1857. On the stability of loose earth.
Philosophical
Transactions of the Royal Society of London
, 147(1 January): 9–27.
Sadrekarimi, A. 2009. Development of a new ring shear apparatus for
investigating the critical state of sands.
Ph.D. Thesis, University of
Illinois, Urbana-Champaign.
Salman, F.A. Al-Shakarchi, Y.J. Husain, H.M. and Sabre, D.K., 2010.
Distribution of earth pressure behind retaining walls considering
different approaches.
International Journal of the Physical Sciences
Vol. 5(9), pp. 1389-1400.
Sherif, M.A. Fang, Y.S. and Sherif, R.I. 1984. Ka and K
0
behind
rotating and non-yielding walls.
Journal of Geotechnical
Engineering
, 110(1): 41–56.
Terzaghi, K. 1934. Large retaining-wall tests: I – Pressure of dry sand.
Engineering News–Record
, 85(1 February): 136–140.


