795
Technical Committee 103 /
Comité technique 103
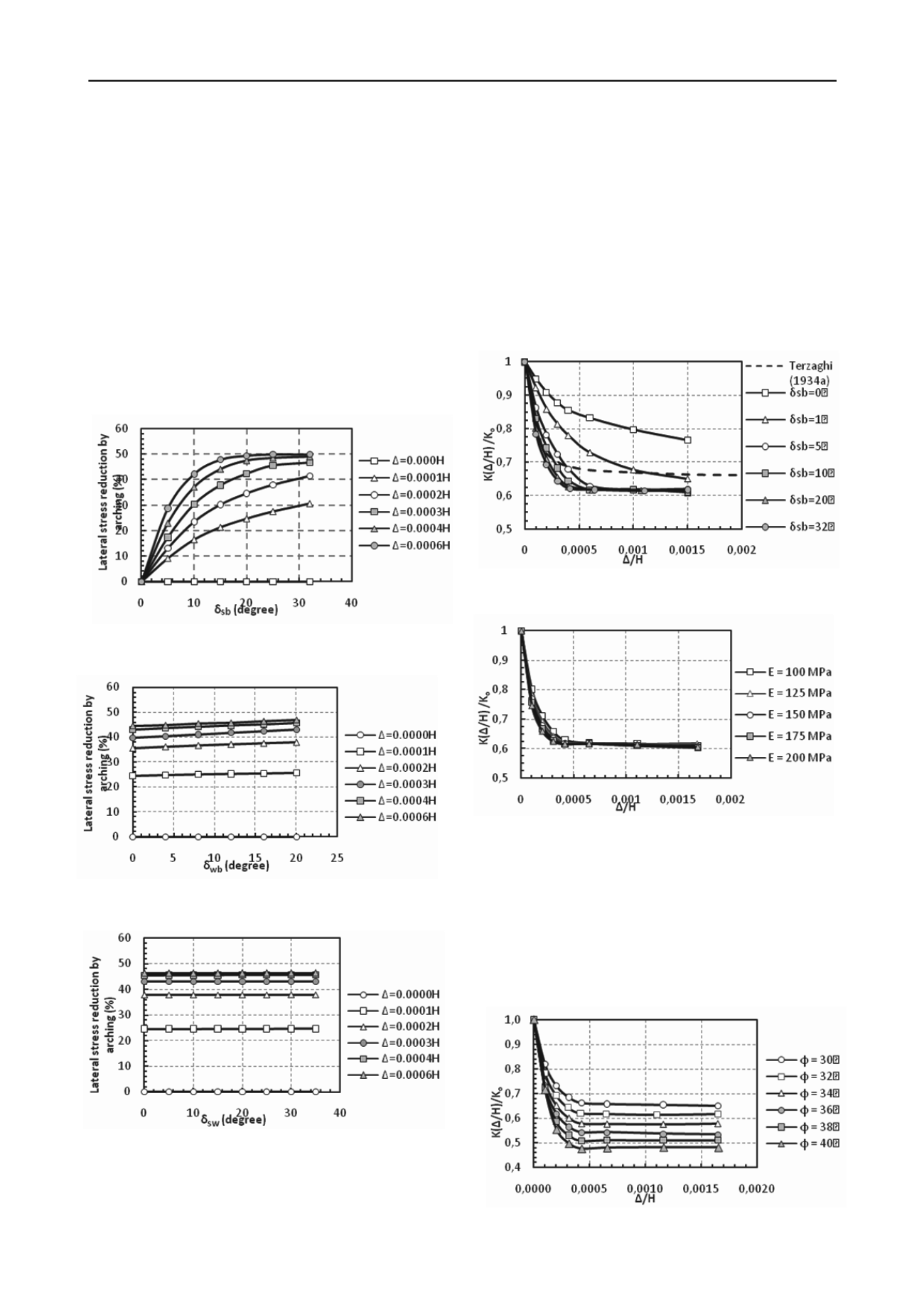
stress reduction increases with increasing wall displacement and
δ
sb
whereas δ
wb
and δ
sw
have no substantial effect on arching.
Figure 4 clearly indicates that there is no effect of backfill soil
arching for δ
sb
= 0
o
and
Δ
= 0.0000H conditions. Thus,
Coulomb’s method could be considered as a special case for
which δ
sb
= 0
o
. However,
Δ
= 0.0000H (absolute at-rest
condition) may not be practically possible as any yielding wall
would slightly move during construction and backfilling,
causing significant horizontal stress reduction. According to
Figure 4, for a backfill and subsoil of the same sand (
ϕ
' = δ
sb
) a
horizontal stress reduction of at least 30% is a prudent
assumption (as
ϕ
' ≈ 30
o
- 34
o
for most sandy soils).
The influence of soil arching on lateral stress reduction is
quantified as the ratio of (p
a
– p
i
) to p
i
, in which p
a
is the lateral
stress at wall’s base that includes the effect of soil arching and
p
i
is the lateral stress that would have developed without any
backfill soil arching. p
i
is obtained by the linear extension of the
lateral stress distribution curve down to wall’s base.
Figure 4: Arching-induced lateral stress reduction for
wb
= 20
o
at
different magnitudes of wall translation and
sb
Figure 6: Arching-induced lateral stress reduction for
sb
= 32
o
and
wb
= 20
o
at different magnitudes of wall movement and
sw
Figure. 7: Effect of wall movement and
sb
on K(
/H)/K
o
for
retaining walls with
wb
= 20
o
and
sw
= 15
o
Figure 8: Effect of wall movement and backfill modulus (E) on
K(
/H)/K
0
for retaining walls with
wb
= 20
o
,
sw
= 15
o
and
sb
= 32
o
Figure 9: Effect of wall movement and soil’s friction angle (
ϕ
) on
K(
/H)/K
0
for retaining walls with
wb
= 20
o
,
sw
= 15
o
and
sb
= 32
o
Figures 7 and 8 show the influence of δ
sb
and backfill soil
modulus (E) on lateral stress reduction and the mobilization of
an active state with wall movement (
Δ
), respectively. Lateral
stress reduction is characterized by the ratio of the horizontal
earth pressure coefficient at a particular wall movement, K(
Δ
/H)
to the at-rest horizontal pressure coefficient (K
o
). K(
Δ
/H) is
obtained by normalizing total lateral thrust by γH
2
/2. By
increasing δ
sb
, the rate and the magnitude of horizontal earth
pressure reduction significantly increase and converge for
δ
sb
> 5
o
. The effect of wall movement (
Δ
/H) on horizontal stress
reduction is most significant for
Δ
/H < 0.0005, after which it
levels off as an active condition is mobilized. An active state
(K(
Δ
/H)/K
o
) ≈ 0.61) is reached at smaller
Δ
/H as δ
sb
increases,
or in other words a greater δ
sb
would limit the amount of wall
movement required to reach an active failure state in the backfill
soil. Figure 8 illustrates that the mobilization of an active failure
condition is fairly independent of backfill soil modulus.
The influence of soil’s friction angle on the mobilization of
an active state is presented in Figure 9. The results show that
the amount of displacement that is required to mobilize an
active state is independent of soil’s internal friction angle which
agrees with findings from physical model experiments (Sherif et
al 1984). The results further show that the active horizontal
earth pressure coefficient decreases by increasing soil’s friction
angle.
Figure 5: Arching-induced lateral stress reduction for
sb
= 32
o
and
sw
= 15
o
at different magnitudes of wall translation and
wb


