675
Technical Committee 103 /
Comité technique 103
M
1
= G{
1
}/G{
stat
}
(11)
K
f,1
= M
1
. K
f
(stat)
(12)
On continue par itérations : partant de M
i-1
et de K
f,i-1
, on
obtient M
i
et K
f,i
= M
i
. K
f
(stat) à la i
ème
itération. Il suffit en
général de 4 ou 5 itérations pour obtenir la convergence à mieux
de 1/1000. Avec les données du projet, la valeur finale de M
s’est établie entre 4 et 7, selon les zones et les efforts appliqués,
avec en particulier un rapport G
max
/E
m
très variable.
2.2
Application au projet
Le Tableau 2 montre quelques résultats fournis comme valeurs
de référence pour le projet. Pour les mégapoteaux, un
coefficient d’effet de groupe de 0.75 à 0.8 a été proposé sur la
base des règles du Fascicule 62 titre V du CCTG.
Tableau 2. Exemples de valeurs de référence de la raideur horizontale
La comparaison des valeurs de K
x
issues du modèle
analytique et de celles issues de la modélisation numérique est
fournie en fin du § 3.
Les valeurs de K
x
relatives à un effort moyen F
x
=200kN ont
été retenues, et une fourchette a été appliquée aux valeurs de
référence : K
x
(min)=2/3.K
x
(réf.) et K
x
(max)=1.5 K
x
(réf.). Il a
été proposé de négliger l’amortissement.
A l’issue de l’étude d’interaction, les pieux ont été vérifiés
vis-à-vis de l’effort {N, M, T}, combinant une composante
statique correspondant aux efforts permanents et une
composante dynamique. La variation de ces grandeurs avec la
profondeur le long du pieu est telle que la valeur maximale a
lieu en tête, sauf pour le moment dans le cas du pieu articulé.
Dans le cas général, il est donc aisé de combiner les valeurs en
tête des deux composantes pour obtenir la valeur maximale
résultante. Il n’en va pas de même pour le moment du pieu
articulé en tête, le moment maximal (Eq. 6) a lieu à la
profondeur z
max
=
/4.L
0
, fonction de la longueur élastique L
0
,
et la valeur à la profondeur z dépend aussi de L
0
et elle est
donnée par :
) /
sin( ) /
exp(
)(
0
0
0
Lz
Lz
LF zM
x
(13)
Les longueurs élastiques L
0
étant différentes pour les deux
composantes, il faut associer deux fonctions de z pour
déterminer le moment maximal et sa profondeur correspondant
à la combinaison statique + dynamique.
3 MODELISATION NUMERIQUE – VALIDATION DES
VALEURS DE PROJET
3.1
Méthodologie de calcul
Les impédances de fondation, ou ressorts équivalents, K, sont
définies comme le rapport entre l’effort (force ou moment)
appliqué en tête de fondation P, et le déplacement correspondant
U (translation ou rotation) :
U
PK
(14)
Une méthode statique et une méthode dynamique sont
étudiées conjointement dans le but de calculer les raideurs
dynamiques des fondations sur pieux, en tenant compte à la fois
de la stratification détaillée du sol, du torseur d’effort induit
dans les fondations et des fréquences des modes de réponse de
la structure.
Le logiciel Flac3D (différences finies) (Itasca 2009) est
utilisé pour la modélisation numérique. Une illustration du
modèle est donnée Figure 2.
Tx
Tz
M
condition
diamètre
E
m
G
max
/E
m
en tête
200 kN 400 kN
encastré mégapoteau SO 0.92 m 60 MPa
20
3903 MN/m 3325 MN/m
pieu zone AF 0.52 m 15 MPa
"
162 MN/m 99 MN/m
0.72 m "
"
304 MN/m 239 MN/m
0.92 m "
"
480 MN/m 402 MN/m
pieu zone AD 0.52 m 50 MPa
"
540 MN/m 436 MN/m
articulé
0.72 m "
"
926 MN/m 792 MN/m
0.92 m "
"
1409 MN/m 1238 MN/m
pieu zone AM 0.52 m 70 MPa
"
739 MN/m 612 MN/m
0.72 m "
"
1250 MN/m 1084 MN/m
0.92 m "
"
1890 MN/m 1676 MN/m
F
x
(pieu isolé)
Raideur K
x
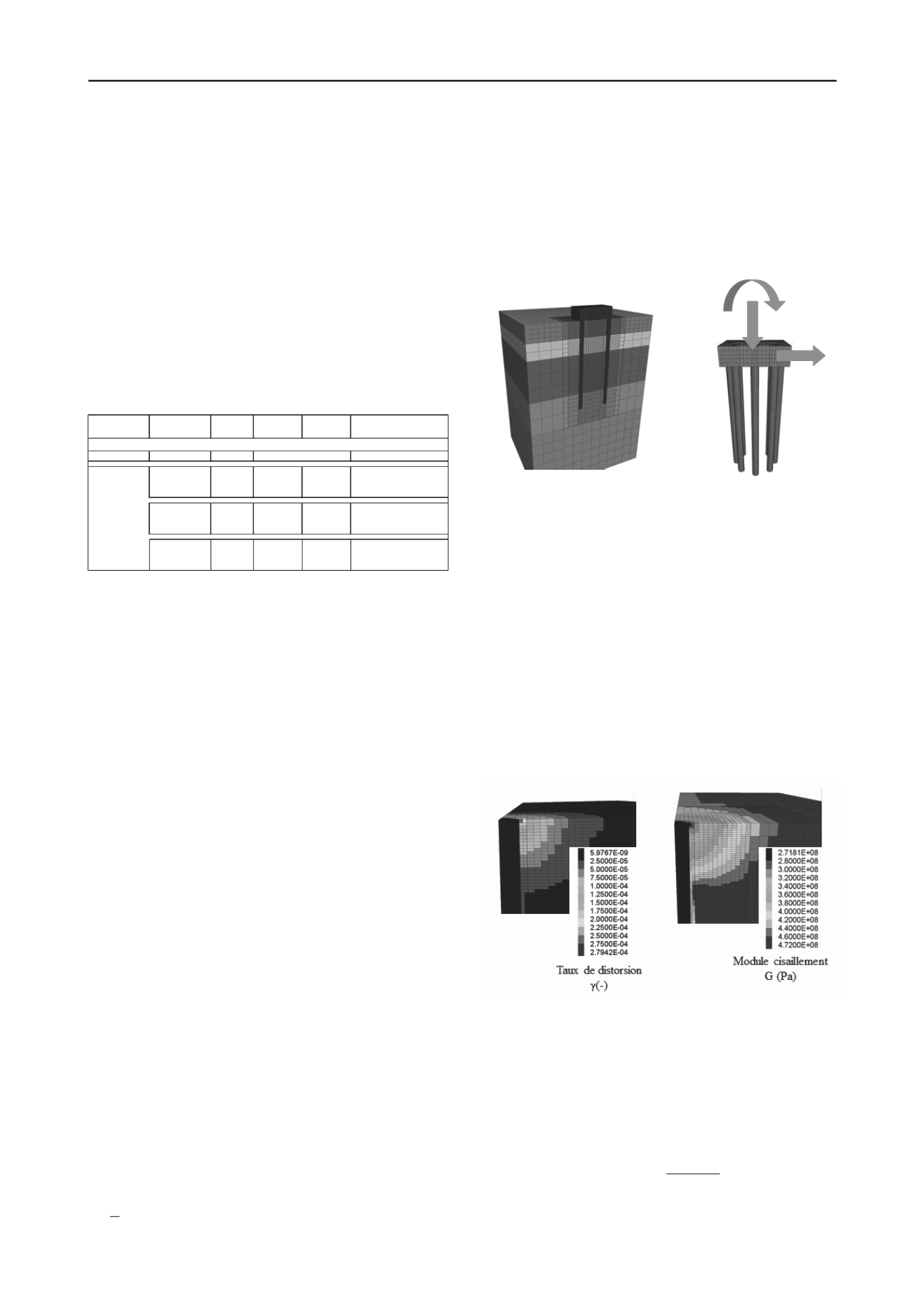
Figure 2. Modèle numérique des fondations constituées d’un groupe de
pieux et représentation d’un torseur appliqué.
Dans le calcul statique, la prise en compte de la non linéarité
du comportement du sol repose sur un processus itératif
permettant d’évaluer, pour un chargement donné, la distorsion
et le module associé dans chaque maille de sol du modèle
numérique 3D, par application de la loi de dégradation
(Figure 1). L’hypothèse d’élasticité est vérifiée a posteriori. La
résistance à la traction dans le sol a été annulée de telle façon
que l’interaction pieu-sol ne fasse pas intervenir de traction. Le
béton des pieux est modélisé par une loi élastique linéaire
caractérisée par les propriétés « instantanées » du béton :
E
béton
= 32 500 MPa ;
ν
béton
= 0.2 ; ρ
béton
= 2500 kg/m
3
.
Les variations du taux de distorsion γ et du module de
cisaillement G dans le sol autour de la tête d’un pieu sont
illustrées Figure 3, dans le cas d’un pieu soumis à un effort
horizontal. A noter que la dégradation du module élastique n’est
significative que sur les premiers mètres de sol (sur une
épaisseur de l’ordre de 2.5 à 5B).
Figure 3. Représentation du taux de distorsion γ et de la dégradation du
module de cisaillement G induit par la non-linéarité du comportement
du sol.
Dans le calcul dynamique, un déplacement harmonique u(t)
de pulsation ω (voir Eq. 15) est imposé en tête de fondation et
la réaction correspondante p(t) est calculée. Les fonctions
d’impédances K(ω) sont des nombres complexes, et sont
définies comme le rapport des transformées de Fourier de la
réaction p(t) et du déplacement imposé u(t) (Eq. 15).
t
A tu
.
sin.
(15)
)(
Dans ce contexte, la fondation est représentée par un ressort
couplé à un amortisseur, définis pour chaque pulsation testée.
)
(
K
(
)
tu TF
tp TF


