670
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
where
,sin
m
f
j
=
sin
m
f
j
¶ ¶
. When
1
m
h
=
, Equations (4) and
(16) are identical which means that all strains are then plastic.
As shown in Figure 5 the isochoric stress paths now start
drifting early towards triaxial extension and compression
modes. As plasticity starts early on, the drift is severe in the
case of this simple hardening model. A drift of such an extent is
not observed experimentally.
Associated flow rule can be retrieved by putting
0
0
c
j
=
such
that
m m
y j
=
. The plots shown in Figure 5 demonstrate that
associated flow rule is not a solution to the drift problem.
Moreover, isochoric effective stress paths in the
p-q
plane are
highly unrealistic.
5 RADIAL MAPPING AND A POSSIBLE
GENERALIZATION
Radial mapping has been used by a number of authors (
e.g
.,
Benz 2007, Tsegaye
1
2010, Tsegaye
et al
. 2012). The
implication of radial mapping is next investigated for the
elastoplastic models considered in sections 3 and 4.
5.1 Isotropy and radial mapping
As shown herein before, Mohr-Coulomb type plastic potential
function introduces unrealistic drift in stress path for radial
strain increments. For an initially isotropic state, such a drift is
not supported by experiments. True triaxial tests show that for
an initially isotropic state and proportional loading, stress paths
are nearly radial. Hence, radial mapping may be a reasonable
assumption. Radial mapping can be interpreted that plastic
strains orient themselves towards isotropic stress state (
i.e
.,
radial to the hydrostatic axis). Coaxiality is maintained between
principal strain increments and principal stresses for radially
proportional loading paths.
Radial mapping can be easily achieved by considering Lode
angle independent potential functions. For pressure sensitive
materials like soils a function of the Drucker-Prager type,
ensures radial return.
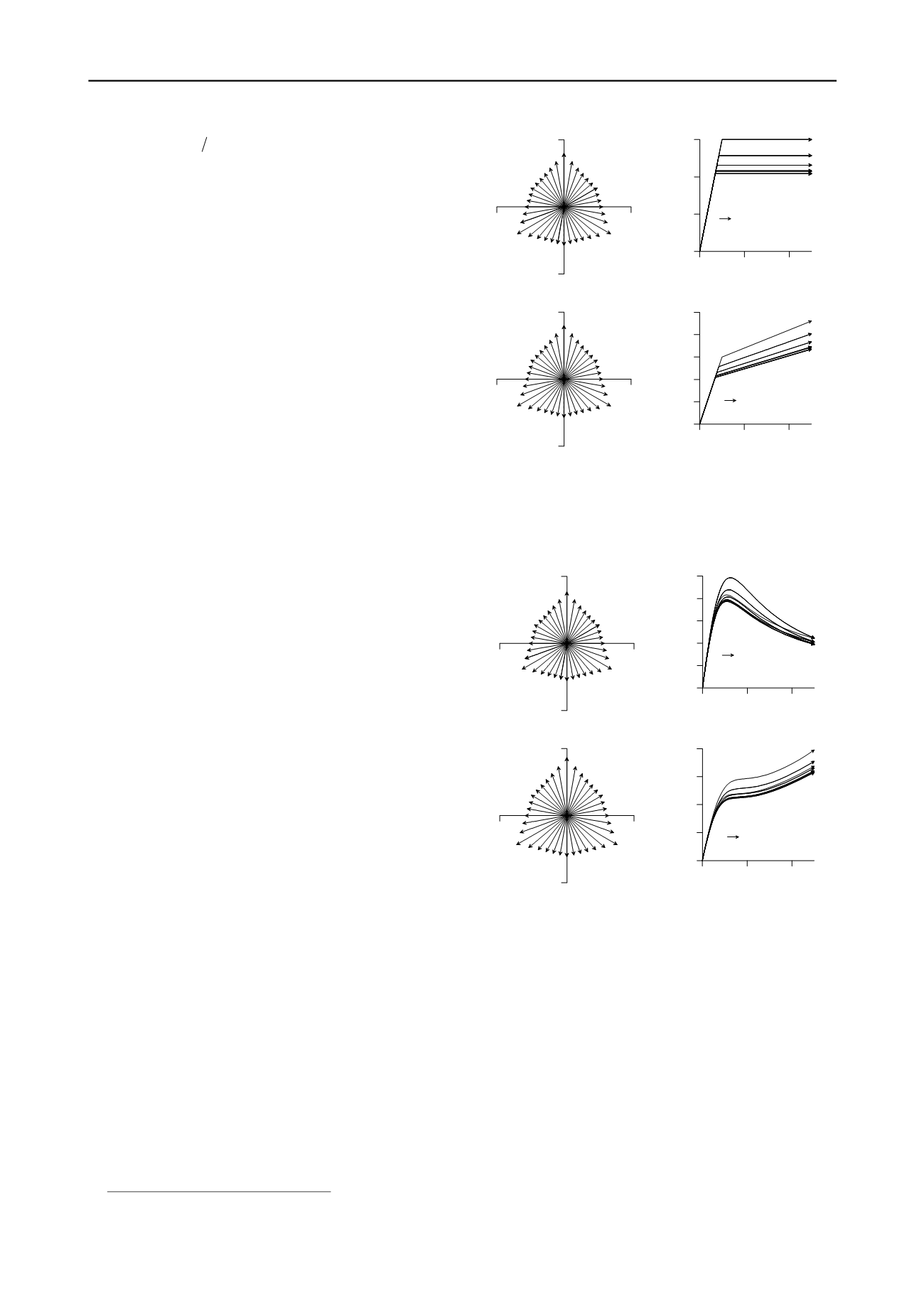
In Figure 6, responses of an elastic perfectly plastic model with
a Mohr-Coulomb yield function and Drucker-Prager plastic
potential function are plotted. As shown in the plots, isotropic
radial strain increments produce radial stress paths. There is no
deviatoric drift. The strength variation in between triaxial
extension and compression is captured. Notice, however, the
minimum strength is not due to triaxial extension but an in-
between state that is located at the shortest distance from the
hydrostatic axis. Figure 7 illustrates response of the simple
hardening model with a Drucker-Prager plastic potential
function to isochoric radial strain increments. The response in
the deviatoric plane remains radial and the plots in
p-q
plane
and
-q
plane are smooth.
5.2 Anisotropy and radial mapping
Anisotropy can be due to fabric constraint and/or induced by
loading history, for example during deposition. It is important to
remark here that if a generalization is to be made, at this stage it
rests on very limited experimental data. For example
considering the tests by Jafarzadeh
et al.
(2008), if each test was
performed on a sample prepared at a different initial void ratio,
stress path contours at constant deviatoric strain may not give a
correct picture of the deviatoric response contours.
1
Previous papers by the first author are published under the last
name Tsegaye.
-1.5
0
1.5
-1.5
0
1.5
0
0.004 0.008
0
40
80
120
160
200
q
p
=35
0
,
max
=5
0
-1.5
0
1.5
-1.5
0
1.5
0
0.004 0.008
0
40
80
120
q
p
=35
0
,
max
=0
0
Figure 6: Plots of isochoric stress paths (for radial isochoric strain
increments, a) in a deviatoric plane (normalized by mean normal stress)
b)
p-q
plane and c) shear strain deviatoric stress plot, for an elastic
perfectly plastic Mohr-Coulomb model with a Drucker-Prager plastic
potential function. For all simulations G=5000kPa and v=0.3 are used.
-1.5
0
1.5
-1.5
0
1.5
0
0.004 0.008
0
20
40
60
80
q
p
=35
0
,
c
=30
0
-1.5
0
1.5
-1.5
0
1.5
0
0.004 0.008
0
10
20
30
40
50
q
p
=30
0
,
c
=30
0
Figure 7: Effective stress path plots for radial isochoric strain
increments, a) deviatoric plane (normalized by mean normal stress), b)
p-q
plane, c) deviatoric strain-deviatoric stress, for an elastic plastic
Mohr-Coulomb model with Drucker-Prager plastic potential function.
For all simulations G=30000 kPa, G
p
=30000 kPa and v=0.3 are used.
Aside from that, the following observations could be noted.
Initial anisotropy fades away during plastic deformation
At larger mobilizations the critical state surface is not
significantly affected by anisotropy.
The use of radial mapping for anisotropic initial stress state
yields
non-coaxial principal stress and principal strain
increments. Since the direction of plastic strains is
known a priori, the degree of non-coaxiality can be
calculated as a state variable.
fading memory of anisotropy and non-coaxiality with
plastic distortion.


