664
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
dilatancy relationship is. Secondly, the phase transformation
line,
i.e
.,
0
p
v
e
=
requires
1
pt
cv
cv
M M M
c
D
= ³
,
(7)
implying dependence on degree of non-coaxiality.
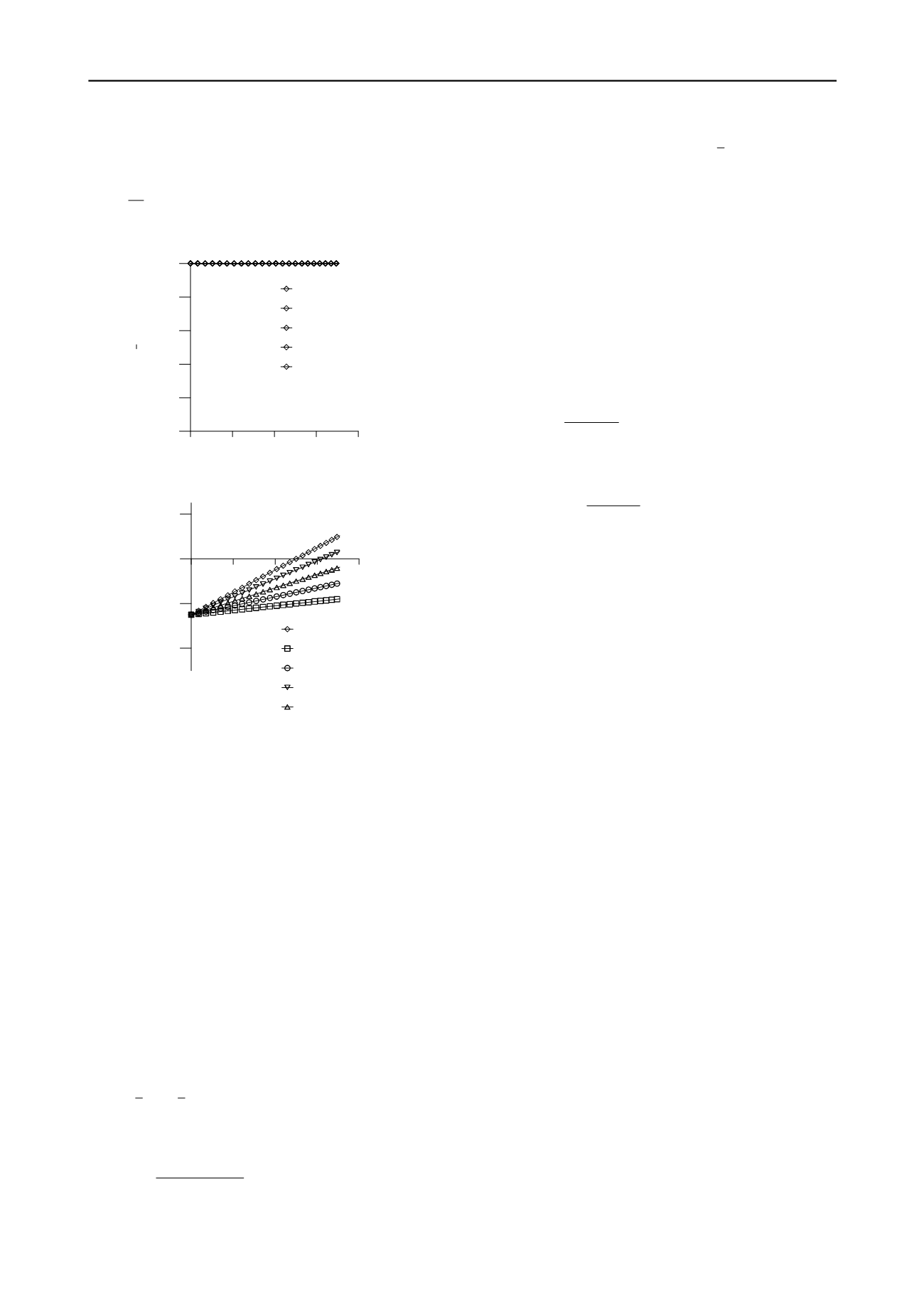
Figure 1: a) Normalized plastic dissipation rate according to the
modified plastic dissipation in Eq. versus mobilized friction angle for
different degrees of non-coaxiality
0
30
c
j
=
, b) Plots of dilatancy ratio
versus stress ratio for different degrees of non-coaxiality, for Eq.
As can be seen from Figure 1
b
, the stress-dilatancy plots
rotate around a value at zero stress ratio. Hence the higher the
degree of non-coaxiality (
i.e
., the less the value of
c
) the higher
the phase transformation stress ratio is; consequently the more
contractive the model behaves.
2.2 Non-coaxiality for Rowe’s stress-dilatancy theory
Rowe (1962) assumed coaxiality between principal stresses and
principal strain rates when he derived his stress-dilatancy
relationship. De Jong (1976) questioned the validity of this
assumption.
Gutierrez and Wang (2009), considering a plane strain
condition, modified Rowe’s (1962) stress-dilatancy theory for
non-coaxiality which when reworked gives a non-coaxial plastic
dissipation according to
(
)
1 1
3 3
sin sin
p
p
p
p
N
m
mR
pc
s e s e
j y g
D
= + =
+
,
(8)
where
sin sin
sin
1 sin sin
m
c
mR
m
c
j j
y
j j
-
=-
-
,
(9)
i
s
are principal stress components and
p
i
e
are the conjugate
plastic strain rate components projected along the principal
stress components (coaxial components),
1
3
p
p
p
g e e
= -
is
plastic shear strain rate and
m
j
is mobilized friction angle; and
c
j
is critical state friction angle. The resulting non-coaxial
stress-dilatancy equation is
ˆ sin
sin
mR
mR
c
y
y
D
=
.
(10)
For
1
c
D
=
and when the interparticle friction angle
m
j
in
terms of the critical state friction angle
c
j
, Rowe’s original
stress-dilatancy relationship is recovered.
From Eq. (8), the maximum plastic dissipation
,max
1 cos
2
sin
p
p c
N
c
pc
j
g
j
D
-
=
,
(11)
occurs when the mobilized friction ratio is
1 cos
sin sin
sin
c
m
mR
c
j
j y
j
-
= =
.
(12)
If Rowe’s stress-dilatancy relationship,
i.e
., Eq. (9) is
approximated by
sin
sin sin
mR
m
c
y j j
» -
.
(13)
such that the plastic dissipation in Eq. (8), simplifies to
sin
p
p
N
c
pc
j g
D
»
.
(14)
The non-coaxial dilatancy angle will then be
(
)
ˆ sin
sin sin
m
m
c
c
y
j j
D
»
-
.
(15)
Unlike the non-coaxial Taylor work hypothesis in Eq. (1)
(Gutierrez and Ishihara 2000), the non-coaxial extension of
Rowe’s stress-dilatancy equation in Eq. (8) (Gutierrez and
Wang 2009) or the simplified form given in Eq. (14) implies
dependence of plastic dissipation on degree of non-coaxiality.
Furthermore, in the non-coaxial extension of Rowe’s stress-
dilatancy equation, the phase transformation remains unaffected
by the degree of non-coaxiality,
i.e
., for
ˆ sin
0
mR
y
=
one
obtains
sin
0
mR
y
=
sin
pt
j
=
sin
c
j
.
For clarity, the normalized plastic dissipation rate and
dilatancy ratio are plotted against the sine of mobilized friction
angle,
sin
m
j
, in Figure 2 for different values of degrees of non-
coaxiality. Comparison of plots in Figure 1 and Figure 2
illustrates that the proposed theoretical modifications given in
Eq. (1) and Eq. (8) fundamentally differ and their difference is
too huge to ignore. This difference has been pointed out in
Tsegaye
et al.
(2012).
0
0.2
0.4
0.6
0.8
sin
m
0
0.1
0.2
0.3
0.4
0.5
D
p
/p
p
c=0.2
c=0.4
c=0.6
c=0.8
c=1
a
0
0.2
0.4
0.6
0.8
sin
m
-0.8
-0.4
0
0.4
-
sin
m
c=0.2
c=0.4
c=0.6
c=0.8
c=1
b


