665
Technical Committee 103 /
Comité technique 103
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
0 0.2 0.4 0.6 0.8
sin
m
0
0.1
0.2
0.3
0.4
0.5
D
p
/p
p
c=0.2
c=0.4
c=0.6
c=0.8
c=1
a
0 0.2 0.4 0.6 0.8
sin
m
-0.8
-0.4
0
0.4
f
c=0.2
c=0.4
c=0.6
c=0.8
c=1
a
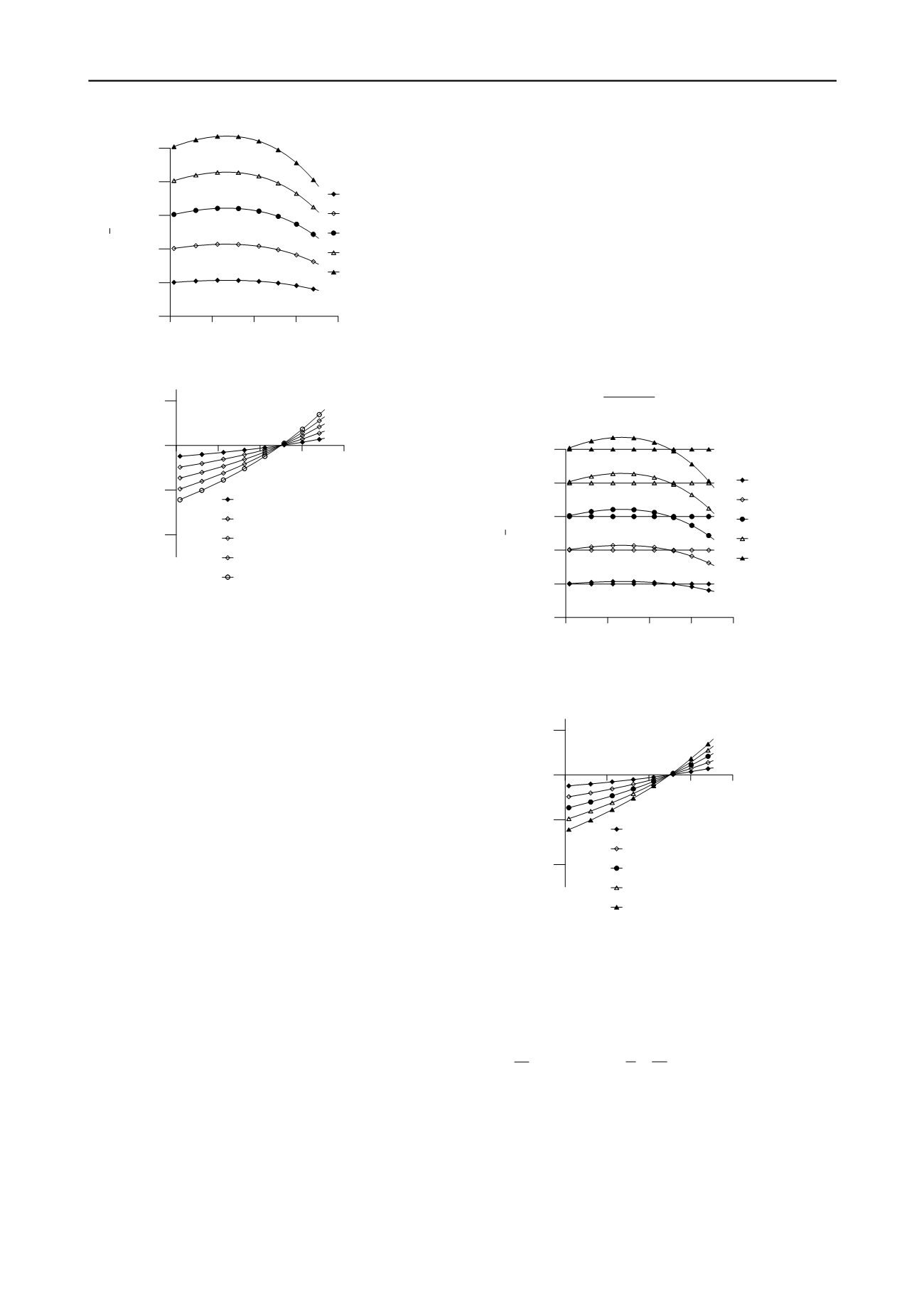
Figure 2: a) Normalized plastic dissipation rate according to the
modified plastic dissipation in Eq. versus mobilized friction angle for
different degrees of non-coaxiality
0
30
c
j
=
; b) Plots of dilatancy ratio
versus stress ratio for different degrees of non-coaxiality, for Eq.
2.3 Proposal of a possible reconciliation
The two approaches, as demonstrated for plane strain
deformation mode, are not consistent with each other. The
selection of one over the other may require experimental
evidences. The authors do not come across sufficient
experimental data to clearly choose one over the other. It is,
however, self evident that both cannot hold to describe the same
phenomenon. The authors propose an alternative work
hypothesis,
s
m
p
p
M
cv q
pc M
e
D
=
,
(16)
such that the difference is reconciled.
There are other ways by which Eq.(16) can be obtained,
which shall not be discussed here. The resulting stress-dilatancy
equation now becomes
(
)
s
m
cv
M c M M
y
s
D
= -
.
(17)
For plane strain deformation mode, Eq. (17) simplifies to
(
)
ˆ sin
sin sin
m
c
m
c
y
j j
D
=- -
.
(18)
The hypotheses put forward by Gutierrez and Ishihara (2000)
and Gutierrez and Wang (2009), amplify the differences
between Taylor’s work hypothesis and Rowe’s minimum
energy hypothesis. However, in the modification proposed here
the difference between Eq.(10) and Eq. (18) is the same as that
of the stress-dilatancy relationship from Taylor’s work
hypothesis and Rowe’s minimum energy ratio hypothesis
(Figure 3).
Note that although for the sake of simplicity a constant
degree of non-coaxiality is used here; various experimental
results demonstrate that the degree of non-coaxiality is an
evolving state variable. Thornton and Zhang (2006) from their
DEM simulations pointed out that “at any stage of shearing,
during simple shear deformation, the angle of non-coaxiality
depends on the mobilized angle of shearing resistance, the rate
of dilation, the initial stress state, and the applied loading path”.
Post bifurcation evolution tendency of degree of non-coaxiality
is controversial. For example, the tests by Vardoulakis and
Georgopoulos (2004) show that degree of non-coaxiality
vanishes even during post bifurcation deformation whereas
Gutierrez and Vardoulakis (2007) show that degree of non-
coaxiality increases during post bifurcation deformation
The authors find a semi-empirical equation for evolution of
degree of non-coaxiality with stress ratio, for plane strain
deformation mode, as
(
)
1
2
1
R
N
c
c
c
N
C N
s
s
d
p
d
D
D
D D
=
-
+
,
(19)
0 0.2 0.4 0.6 0.8
sin
m
0
0.1
0.2
0.3
0.4
0.5
D
p
/p
p
c=0.2
c=0.4
c=0.6
c=0.8
c=1
a
0 0.2 0.4 0.6 0.8
sin
m
-0.8
-0.4
0
0.4
-
sin
m
c=0.2
c=0.4
c=0.6
c=0.8
c=1
a
Figure 3: a) Normalized plastic dissipation rate according to the
modified plastic dissipation in Eq. versus mobilized friction angle for
different degrees of non-coaxiality
0
30
c
j
=
; b) Plots of dilatancy ratio
versus stress ratio for different degrees of non-coaxiality, for Eq.(18)
where
1
3
N
s
s
s
=
and
2
tan
4 2
c
N
C
p j
æ
ö÷
ç
= + ÷
ç
÷÷
çè
ø
(20)
and
R
D
is a parameter that controls the rate at which the initial
degree of non-coaxiality vanishes with stress ratio, Figure 4.
The equation implies that non-coaxiality vanishes with stress
ratio and increases when
0
N
s
d
<
. See for example Roscoe
(1970), Arthur
et al.
(1986) for experimental justification.
b
b


