661
Technical Committee 103 /
Comité technique 103
l’enveloppe de rupture en cisaillement, de façon similaire à celle
présentée dans le paragraphe précédent.
Figure 3. Schématisation du modèle de l’armature dans FLAC.
Une armature est discrétisée en plusieurs segments, régis par
le modèle
« strip »
. Le glissement de l’armature par rapport au
sol est le résultat d’une saturation du cisaillement sur un
ensemble de segments. Cette saturation est elle-même contrôlée
par plusieurs paramètres tels que la distribution instantanée de
la contrainte verticale, le niveau instantané de déplacement
relatif, la raideur du sol ainsi que la raideur du renforcement.
3.2
Modélisation d’un essai d’extraction sous chargement
dynamique cyclique
Afin de mieux comprendre les mécanismes en jeu lors d’un
essai d’extraction sous chargement dynamique, la configuration
de l’ouvrage expérimental de Rouen a été modélisée et l’essai
d’extraction a été simulé numériquement. L’objectif étant dans
un premier temps de comprendre le phénomène de mobilisation
à l’échelle locale, les paramètres du modèle « armature »
(raideur d’interface et critères de glissement) n’ont pas été calés
pour représenter les essais de Rouen. La raideur d’interface
utilisée pour les chargements statiques ainsi que les valeurs
normatives du coefficient d’interaction ont été attribuées aux
paramètres d’interfaces sol-armature.
Un essai d’extraction correspond à un chargement artificiel
bien spécifique imposé à l’armature. Cette dernière est soumise
à une vitesse d’extraction constante et faible (1mm/min selon
NF P 94-222:1995). Pendant l’extraction, le déplacement de
l’armature en tête et la résistance d’ancrage sont enregistrés.
Ces conditions peuvent être reproduites grâce à l’option
dynamique
du logiciel FLAC.
3.2.1
Analyse du cisaillement à l’échelle locale
Au début de l’essai simulé, la résistance d’ancrage croît alors
en même temps que le déplacement de la tête de l’armature.
Puis la résistance atteint un pallier à partir duquel la résistance
d’ancrage est sensiblement constante alors que l’armature se
déplace globalement par rapport au sol.
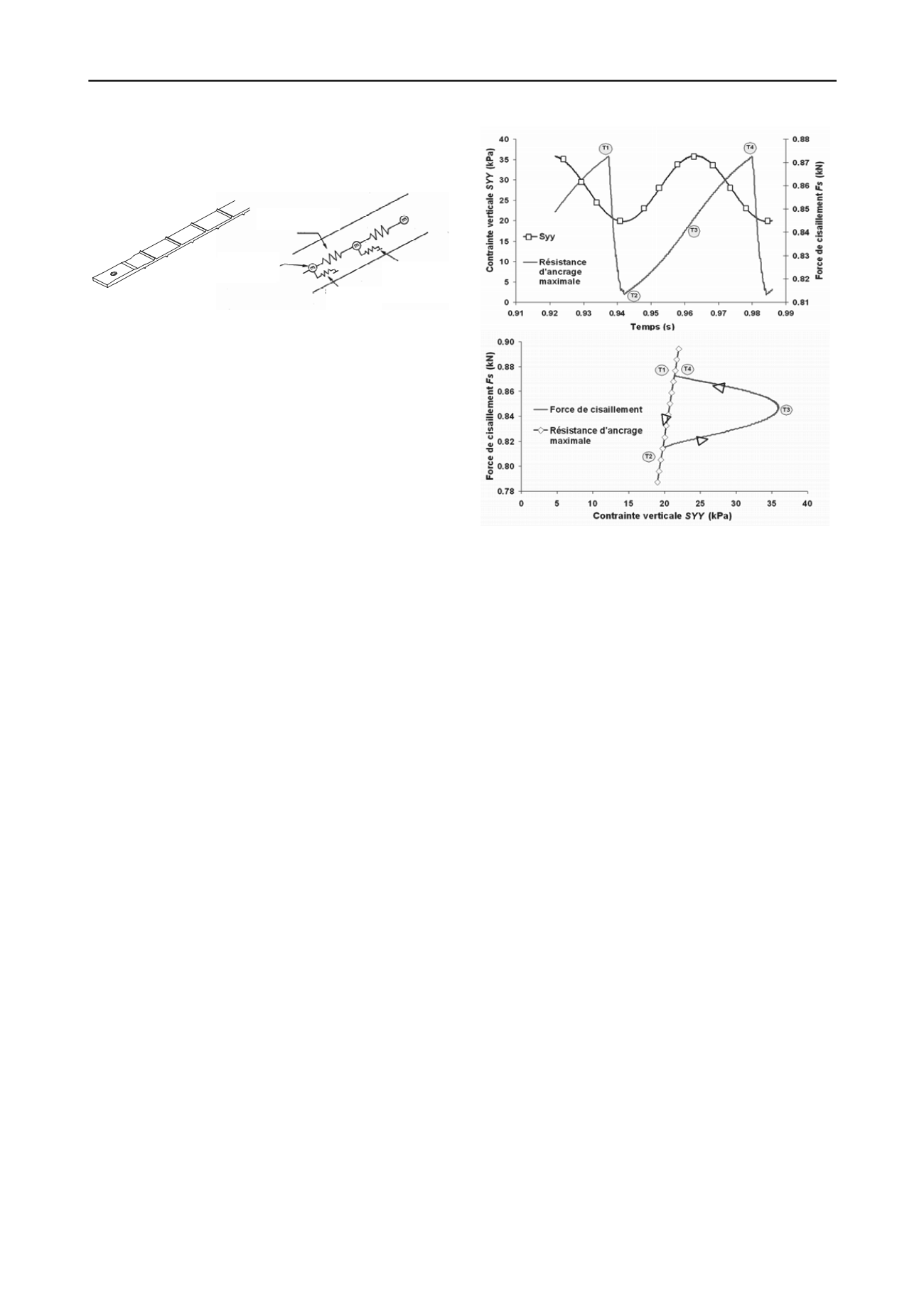
Dans cette phase, l’étude fine du cisaillement au niveau
d’un des segments permet de bien mettre en évidence
l’évolution de la résistance d’ancrage locale pendant la phase de
glissement de l’armature (cf. figure 4). Les conclusions de
l’analyse sont les suivantes :
-
la résistance de cisaillement croît progressivement
jusqu’à ce que la contrainte verticale atteigne son
minimum cyclique (T1)
-
le cisaillement chute alors brutalement, indiquant une
perte d’adhérence locale momentanée (T2)
-
puis la contrainte verticale augmente à nouveau et une
reprise d’adhérence est constatée sur le modèle (T3)
Les conclusions de cette première étude sont en accord avec
celles obtenues par Murray et
al
(1979) indiquant que la
diminution de la résistance d’ancrage correspond à un
allégement de la contrainte verticale. En effet, l’étude montre
que c’est à la fin de la phase de déchargement, quand la
contrainte verticale atteint son minimum cyclique, que le
glissement a lieu.
a)
Figure 4. Evolution de l’effort de cisaillement et de la contrainte
verticale au niveau d’un segment d’armature : a) Evolution instantanée
du cisaillement et de la contrainte verticale en fonction du temps, b)
Evolution du cisaillement en fonction de la contrainte verticale avec
superposition de l’enveloppe de rupture.
Il semble important de noter que les conclusions de cette
première étude numérique sont indépendantes des paramètres
du modèle numérique. Plusieurs simulations, pour différentes
fréquences de sollicitations, et pour différents paramètres
géotechniques (modules de sols, amortissements, etc.) apportent
les mêmes conclusions.
3.2.2
Estimation de l’adhérence sous chargement dynamique
cyclique : un phénomène de « chenille »
Cette première simulation permet de conclure que la
résistance d’ancrage lors d’un essai d’extraction est déterminée
par le minimum local atteint par la contrainte appliquée le long
de l’armature au cours du chargement dynamique, et non par la
contrainte moyenne.
En dynamique, la contrainte de cisaillement mobilisable à
l’instant
t
, à
une abscisse
x
est donnée par la relation suivante :
tx
tx
tx
v
v
,
'
,
'
,
'
*
max
(4)
Ainsi la résistance à l’extraction sous chargement sinusoïdal
entre
t=0
et la période
T
du signal peut être définie par la
relation :
L
LLx
min v
min v
kf
a
dx x
x
b
R
'
'
2
*
;
(5)
avec
σ’
vmin
(x
) la contrainte verticale minimale à l’abscisse
x
le long de l’armature au cours du cycle.
En raison de la vitesse de propagation des ondes de
cisaillement et de compression dans le sol, la contrainte
verticale minimale
σ
vmin
(x
) n’est pas atteinte à l’instant où la
sollicitation sur la voie est minimale, mais avec un décalage
temporel. Par ailleurs, le minimum de contrainte vertical locale
n’est pas atteint simultanément tout au long de l’armature (du
fait de la vitesse de propagation des ondes de compression dans
le sol). Le glissement sol/armature n’est donc pas simultané sur
toute sa longueur, mais progressif. Le comportement de
b)
Raideur axial
Nœud
Armature HA
Raideur de
l’interface
Critère de
glissement


