674
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
m
stat
E E
.2
) 1.(2
stat
stat
E
G
(1)
Le paramètre
est le coefficient rhéologique de la méthode
pressiométrique. Le coefficient de Poisson
a été fixé à 0.33.
Dans le domaine des très petites déformations, de l’ordre de
10
-5
, les essais cross-hole permettent de déduire le module de
cisaillement maximal G
max
et le coefficient de Poisson
ν
à partir
des vitesses des ondes de cisaillement V
s
et de compression V
p
,
et de la masse volumique
selon les Equations 2.
2
max
.
S
V G
2 2
2 2
/
22
/
2
s
p
s
p
VV
VV
(2)
La corrélation entre G
max
et le module pressiométrique E
m
a
donné dans la majorité des cas un rapport G
max
/E
m
d’environ 9,
valeur classique, mais, en partie supérieure de l’horizon
crayeux, on a observé sur deux sondages, entre 5m et 15m de
profondeur, des valeurs plus élevées, de 20 ou plus.
Les propriétés mécaniques permettant de caractériser la
déformabilité des matériaux en « statique » ou à très petites
déformations sont récapitulées dans le Tableau 1 pour la zone
Sud, une des 3 zones définies à partir des sondages cross-hole.
Un zonage plus précis, comportant 7 zones, a été établi à partir
des sondages pressiométriques.
Tableau 1. Synthèse du modèle géotechnique défini pour la zone Sud de
’ouvrage.
l
Craie
tendre
Craie
sableuse
Marne1
Marne
2
Epaisseur
(m)
7
8
8
-
ρ (kg/m
3
)
1800
1900
2000
2000
V
s
(m/s)
510
870
830
640
G
max
(MPa)
470
1440
1380
820
ν (-)
0.38
0.38
0.42
0.44
E
m
(MPa)
50
120
150
150
α (-)
1/2
2/3
2/3
2/3
E
stat
(MPa)
200
360
460
460
G
stat
(MPa)
70
130
160
160
6.0
) ;6.0max(
65.2
) ;6.0max(
6.0
3
4
12
) (
B
B
E
stat
K
m
f
Pour les déformations intermédiaires, on fait appel à une
interpolation suivant une loi dite de dégradation des modules,
indiquée ci-après.
1.4
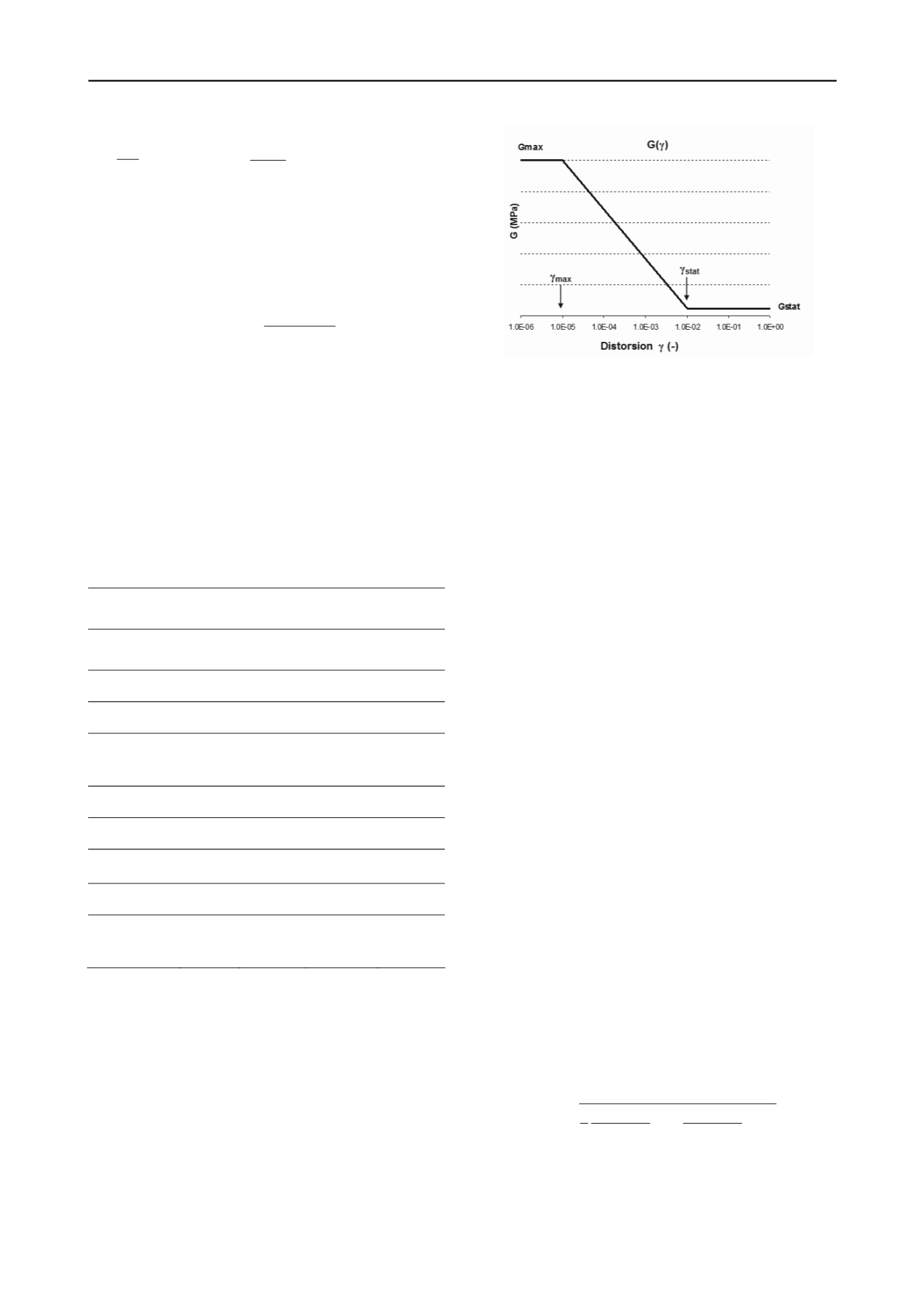
Loi de dégradation des modules
Pour les deux approches, méthode analytique et modélisation
numérique, et à défaut de données bibliographiques concernant
l’évolution du module élastique dans les craies et les marnes, la
loi simplifiée illustrée à la Figure 1 a été retenue pour tous les
sols. Les seuils de distorsion sont : γ
max
= 10
-5
et γ
stat
= 10
-2
.
Dans ces conditions, la loi est caractéristique d’un matériau de
type « sable » ou « argile peu plastique ».
Figure 1. Loi de dégradation des modules simplifiée.
2 METHODE ANALYTIQUE – VALEURS DE PROJET
2.1
Méthodologie de calcul
Dans la méthode analytique, l’évaluation de l’impédance
horizontale K
x
a été développée à partir de deux bases :
a) La solution du pieu infiniment long, de diamètre B, soumis
à une charge horizontale F
x
en tête, avec un module de
réaction k constant, reliant à une profondeur donnée la
réaction p et le déplacement horizontal u
x
. Le pieu est soit
articulé en tête, soit encastré dans le chevêtre sans rotation.
p=k.u
x
ou
p=K
f
/B.u
x
(3)
b) L’étude théorique du mécanisme de réaction latérale des
pieux (Baguelin, Frank, Saïd, 1977).
La solution (a) donne la longueur élastique de transfert L
0
et
le déplacement en tête u
x0
, le moment maximal M
max
, et
l’impédance K
x
, en fonction de K
f
, du module du béton du
pieu E
b
(=30000 MPa) et du module d’inertie I (=
B
4
/64):
L
0
= [4 E
b
.I/K
f
]
0.25
(4)
u
x0
= n F
x
/L
0
/K
f
n={2 ;1}
(5)
M
max
= m F
x
L
0
m={0.32 ;1}
(6)
K
x
= K
f
L
0
/n
n={2 ;1}
(7)
Par convention d’écriture, le paramètre n ou m prend la
première valeur entre crochets {} pour le pieu articulé en tête, la
deuxième valeur pour le pieu encastré en tête.
L’étude (b) donne la distorsion
au bord du pieu et permet
de la relier au déplacement u
x0
. Après diverses transformations
des équations originelles, on obtient les relations :
= u
x0
/B.2(1+
)/
.s
(8)
s = 0.808 +0.265 Ln(k L
0
/B) k={7/15;12/15} (9)
Pour un effort en tête donné F
x
, on tient compte de la non-
linéarité des modules (loi de dégradation) par un processus
itératif. La valeur initiale de K
f
est la valeur statique K
f
(stat)
habituelle (courte durée d’application), donnée par la méthode
pressiométrique, en prenant en compte une valeur moyenne du
module E
m
sur la couche superficielle, sur 2 à 4m d’épaisseur :
(10)
On obtient une première valeur
1
de la distorsion, en
général inférieure à la valeur
stat
du diagramme de la loi
dégradation (Figure 1), ce qui donne un coefficient
multiplicateur M
1
, que l’on applique au module K
f
(stat) :


