262
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
Proceedings of the 18
th
International Conference on Soil Mechanics and Geotechnical Engineering, Paris 2013
4
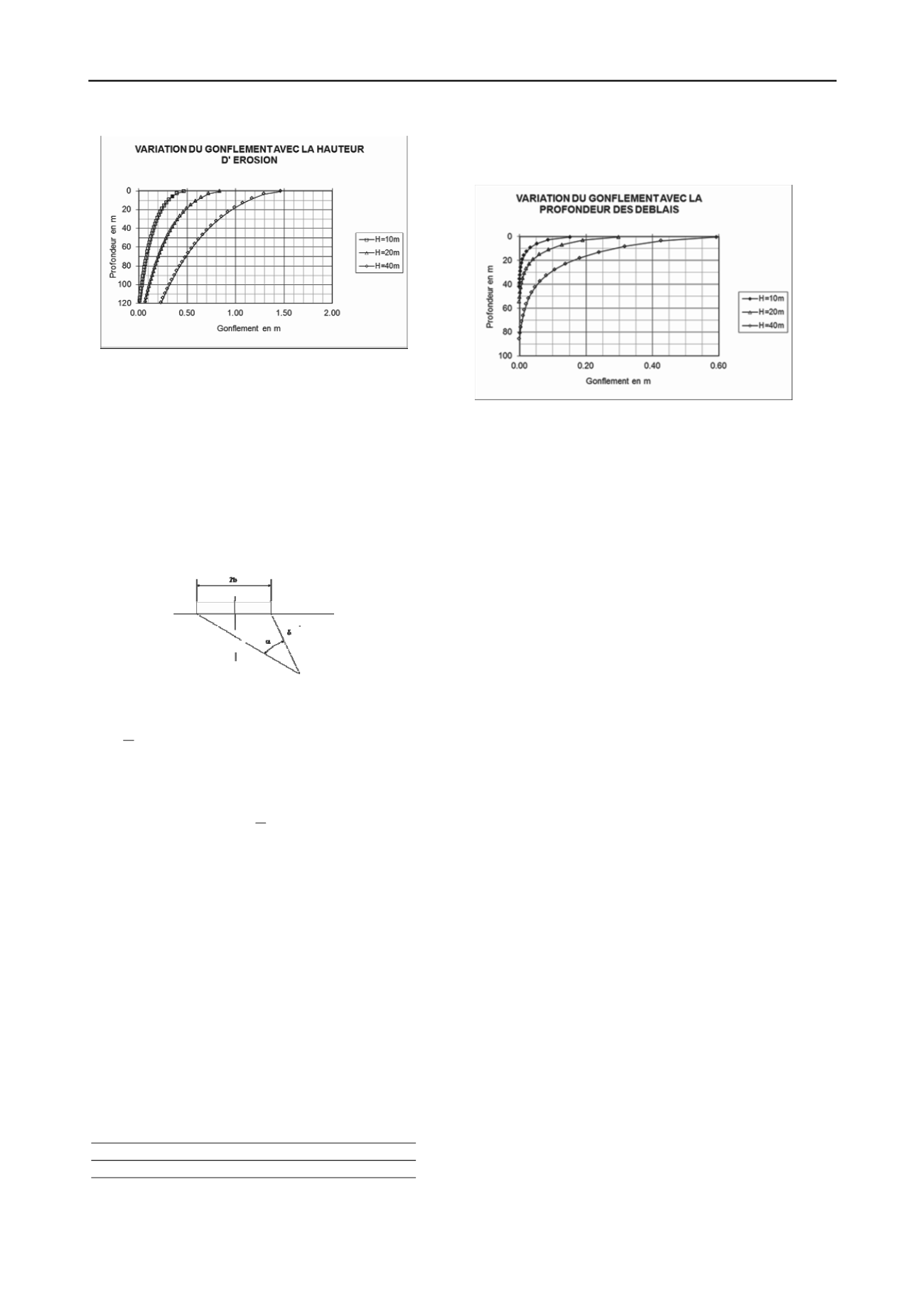
Les résultats des calculs obtenus sont représentés sur le
graphique de la figure 7 ci-dessous.
Figure 5. Résultats des calculs de gonflement pour différentes
hauteurs H d’érosion
.
5. ÉTABLISSEMENT D’UN MODÈLE DE CALCUL
POUR UN DÉBLAI
Figure 7. Résultats des calculs de gonflement pour différentes
profondeurs H de déblai
Dans le cas d’un déblai, le terrassement n’est pas infini.
De ce fait il se produit un amortissement des contraintes
avec la profondeur, comme indiqué ci-après.
Ces résultats montrent que la profondeur d’influence
s’accroît avec la profondeur du déblai. Les amplitudes de
gonflements calculées en fond de déblai pour ces
configurations varient de 0,15 à 0,60 m.
5.1. Effet de la profondeur
Il est à noter qu’afin d’améliorer la prise en compte des
talus du déblai, il est possible de décomposer le déblai en
plusieurs charges rectangulaires épousant la pente du
déblai. Les exemples présentés ici n’intègrent pas cette
décomposition.
Nous allons considérer une charge sur un milieu semi -
infini :
6. CONCLUSION
Les essais œdométriques spécifiques analysés, permettent
de caractériser plus précisément le comportement des sols
surconsolidés au déchargement. Celui-ci se traduit
successivement dans l’espace œdométrique [e ; log
] par
deux droites de pentes respectives
(indice de
gonflement) puis (coefficient de gonflement).
C
s
Figure 6. Méthode de Poulos & Davis
La contrainte verticale s’écrit (Poulos & Davis 1974) :
)2
cos(
sin
p
z
(14)
Ces deux droites se coupent en un point défini par
.
C
g
Dans le cas d’un déblai, le terrain peut être considéré
comme infini de part et d’autre de la tranchée. Cela
entraîne donc :
z
G
A partir de ces essais, il est alors possible de calculer
les gonflements résultant d’un déchargement généralisé
(érosion) ou de la réalisation d’un déblai.
quand
alors
l
2
2
.
Dans le cas de déblai, où la géométrie du déchargement
n’est pas infinie, il convient de tenir compte de
l’amortissement des contraintes avec la profondeur, se
traduisant par des gonflements beaucoup plus faibles que
pour un déchargement généralisé.
A partir de cette relation, il est alors possible de
calculer la variation de contrainte dans l’axe du déblai en
prenant en compte l’influence des deux parties situées de
part et d’autre de ce dernier.
Le cas de sols très fortement surconsolidés, présentant
des pressions de préconsolidation trop élevées pour être
correctement mesurées avec un essai œdométrique
classique, reste encore à étudier et nécessite la mise au
point de méthodes expérimentales spécifiques.
5.2. Résultats des calculs
Au préalable, il convient de noter que dans ce qui suit,
les calculs ne peuvent être réalisés qu’avec la méthode
numérique.
Ils ne sont réalisés que dans le domaine irréversible
compte tenu des profondeurs importantes à atteindre pour
avoir un comportement élastique.
7. REMERCIEMENTS
Remerciements à Guilhem Teulade qui a été à l’origine de
cette réflexion.
Les caractéristiques géométriques du talus prises en
compte sont définies ci-dessous :
8. REFERENCES
T
ableau 2. caractéristiques de déblai prises en compte
LEROUEL S., MAGNAN J.P. & TAVENAS F. remblais sur
argile molle. Lavoisier 1985
Hauteur
déblai (m)
Pente talus
tg
Largeur
plateforme (m)
Largeur équivalente
(m)
10
1/2
20
40
20
1/2
20
60
40
1/2
20
100
MAGNAN J.P. & SERRATRICE J.F. Détermination de la courbe
d'état limite d'une marne. Séminaire « De la Géologie au
calcul des Ouvrages ». Grenoble 6-10 novembre 1995.
POULOS & DAVIS. Elastic Solutions for Soils and Rocks. J.
Wiley 1974.


